今回はちょっと聞き慣れない「くさび形空気層」による光の干渉がテーマです。
明線条件を求める計算自体は回折格子よりも簡単ですが,最大のポイントは光の反射が干渉条件に絡んでくること。
波の反射の種類とその特徴が言えない人は復習してから先に進みましょう。
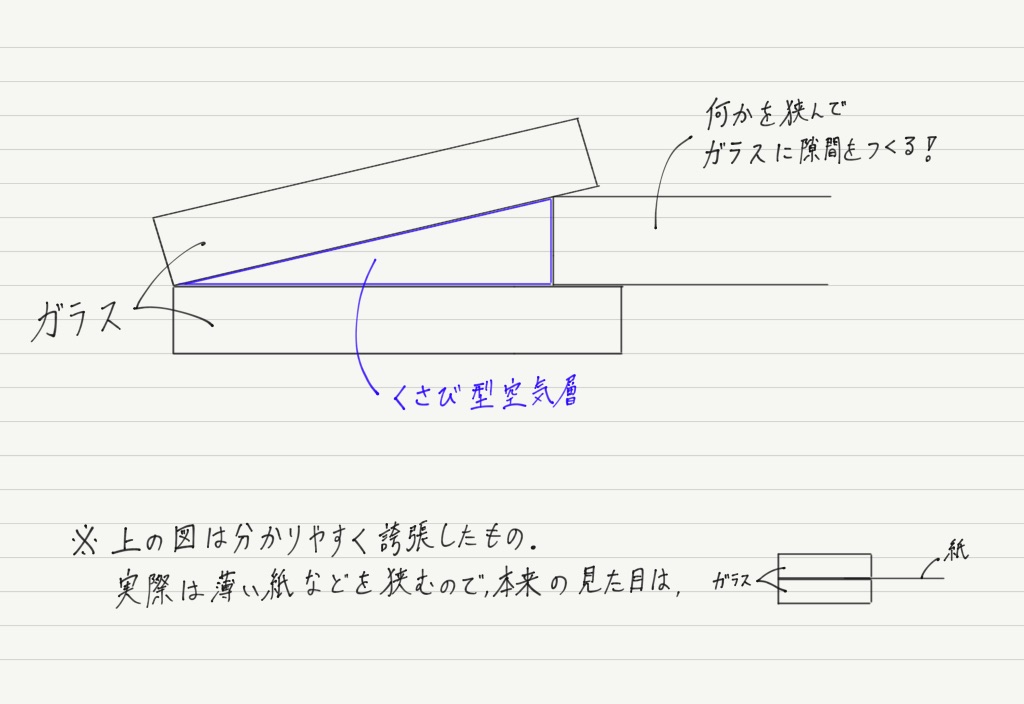
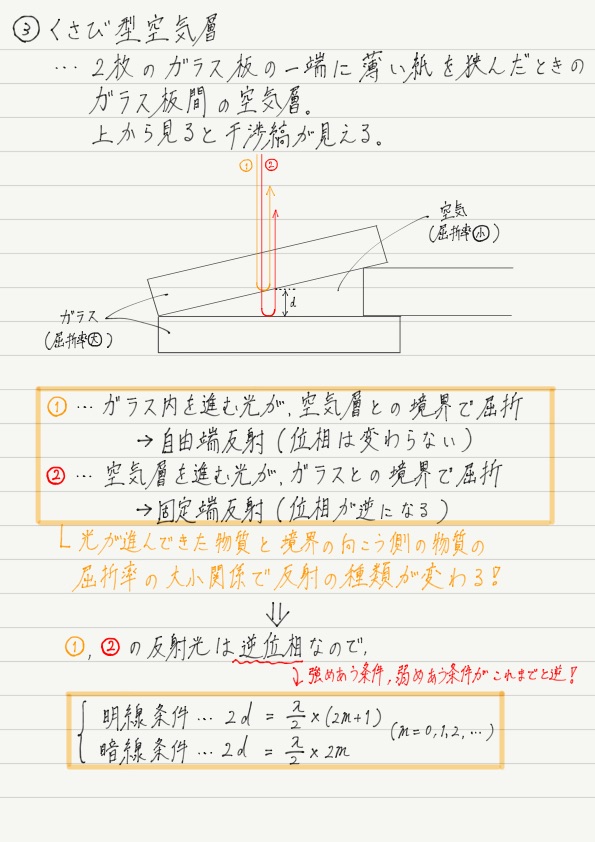
くさび形空気層の構造
「くさび形空気層」という名前はいかつい印象を受けますが,たいしたことはありません。
2枚のガラスの片側に薄い紙などを挟んだときにできる,ガラスの隙間のことです。
くさび形空気層をつくったガラス板を上から見ると,明暗の縞模様が観察できます。
この縞模様はもちろん,光の干渉によって形成されるものです!
となると,明線と暗線の干渉条件がそれぞれどうなるか気になるところ。 さっそく求めてみましょう!
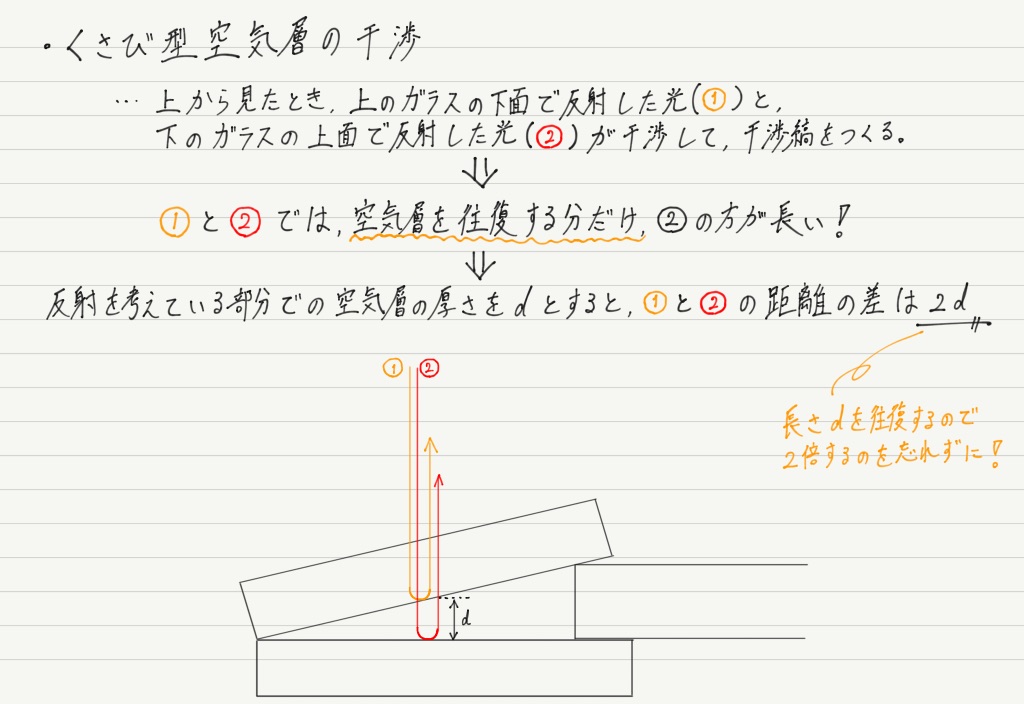
距離の差を求める
干渉条件を求めるには,干渉する2つの光が通る距離の差を求めるところからスタート!
はい,めっちゃ簡単。
ヤングの実験のようなゴチャッとした計算もないし,回折格子のように三角比が出てくるわけでもありません。
てことは,2d = 半波長 × 偶数が明線条件で,2d = 半波長 × 奇数が暗線条件になって,ハイおしまい
…って,ちょっと待ったぁぁぁ!!
今回の干渉は前講までと決定的に異なる点があります。
それはズバリ,干渉する光が途中で反射していること。
これも考慮してあげないといけません!
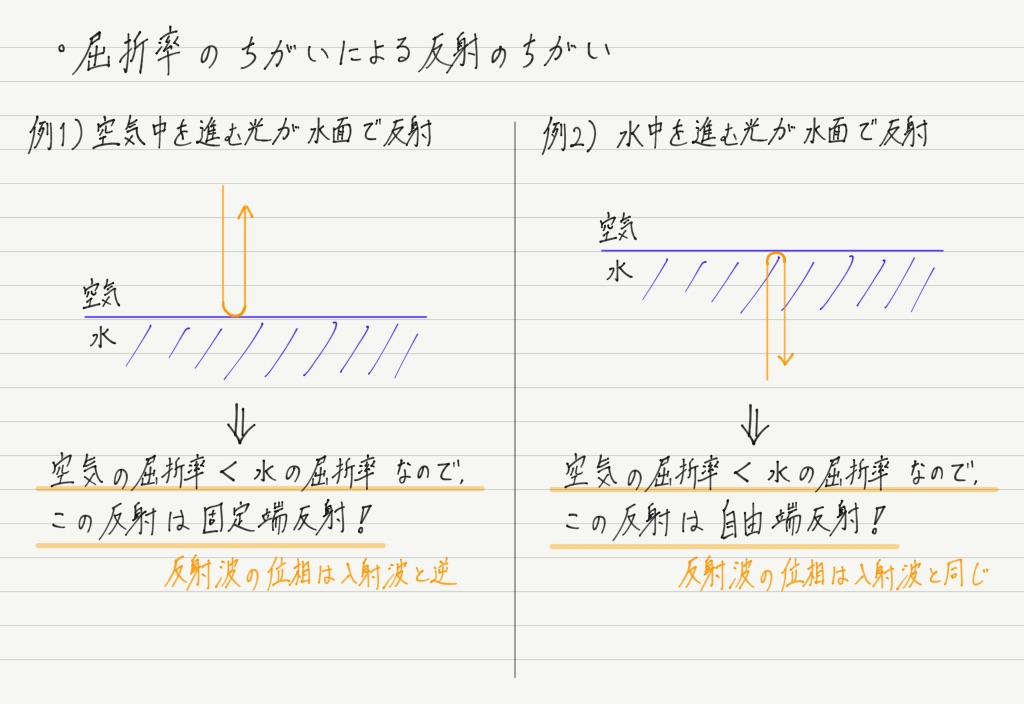
光の反射と屈折率
冒頭で波の反射について復習するように言いましたが,理解はバッチリですか?
波の反射には,反射によって位相が変化しない自由端反射と,位相が逆転する固定端反射の2種類があります。
これは光の反射についても例外ではありません!!
光の場合,反射が自由端か固定端かは比較的簡単に見極められます。
屈折率の小さい物質を進む光が,それよりも屈折率が大きい物質に入ろうとして反射する → 固定端反射
屈折率の大きい物質を進む光が,それよりも屈折率が小さい物質に入ろうとして反射する → 自由端反射
になります!
なぜ屈折率の大小が反射の種類に影響を及ぼすのかは高校物理の範囲では説明できませんが,この結果は知っておかないと問題が解けないのでとりあえず暗記してください。
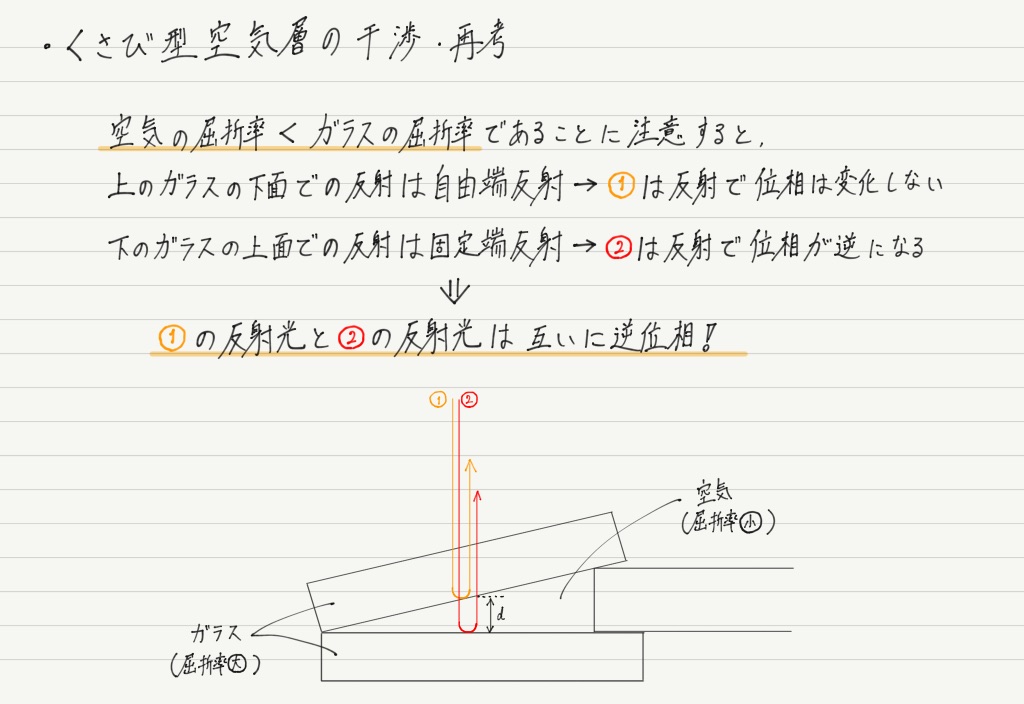
反射がある場合の干渉条件
以上のことを踏まえた上で,再びくさび形空気層について見てみましょう。
上のガラスで反射した光の位相は変化しないけれど,下のガラスで反射した光は逆位相になっている…
ということで,くさび形空気層では逆位相バージョンの干渉条件を適用しなければいけません!
よって,2d = 半波長 × 奇数が明線条件で,2d = 半波長 × 偶数が暗線条件となります。
※ 逆位相バージョンの干渉条件がわからない人はこちらの記事 ↓ のまとめノートを見てください。
くさび形空気層は場所によってdの値が異なるので,明線条件を満たす場所もあれば暗線条件を満たす場所もあり,その結果として干渉縞が浮かび上がるのです。
固定端反射の回数に注意
さて,今回の干渉条件は結果的に「半波長の奇数倍で明線,偶数倍で暗線」という,ヤングの実験や回折格子と逆の条件になりました。
だからといって,「固定端反射をしたら条件は逆」のような安直な丸暗記は応用が効かなくなるので絶対にダメ!!
ちょっとひねった問題だと,固定端反射を複数回行うようなものもあります。
そのような問題では,固定端反射をしたからといって条件が逆になるとは限りません!
同位相ならばこれまで同様,半波長の偶数倍で明線,奇数倍で暗線です。
このように,干渉する光がそれぞれ何回ずつ固定端反射をするかで結果が変わってきます。
図を書いてしっかり見極めることが大事!
今回のまとめノート
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。
次回予告
いよいよ波のラストです。
ラストも光の干渉。 頑張っていきましょう!