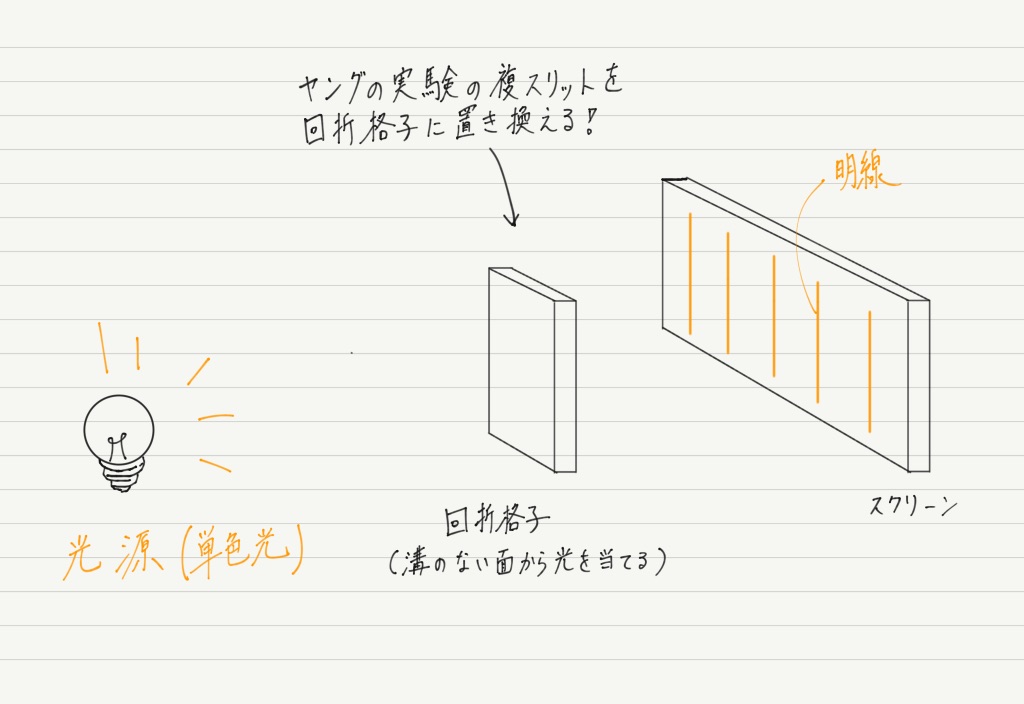
ヤングの実験ではスリットを抜けた光が干渉して明線をつくり出しましたが,スリットの代わりに回折格子と呼ばれるものを用いても明線が生じます。
前回の復習も兼ねて,今回は回折格子の明線条件を明らかにしてみましょう。
回折格子とは
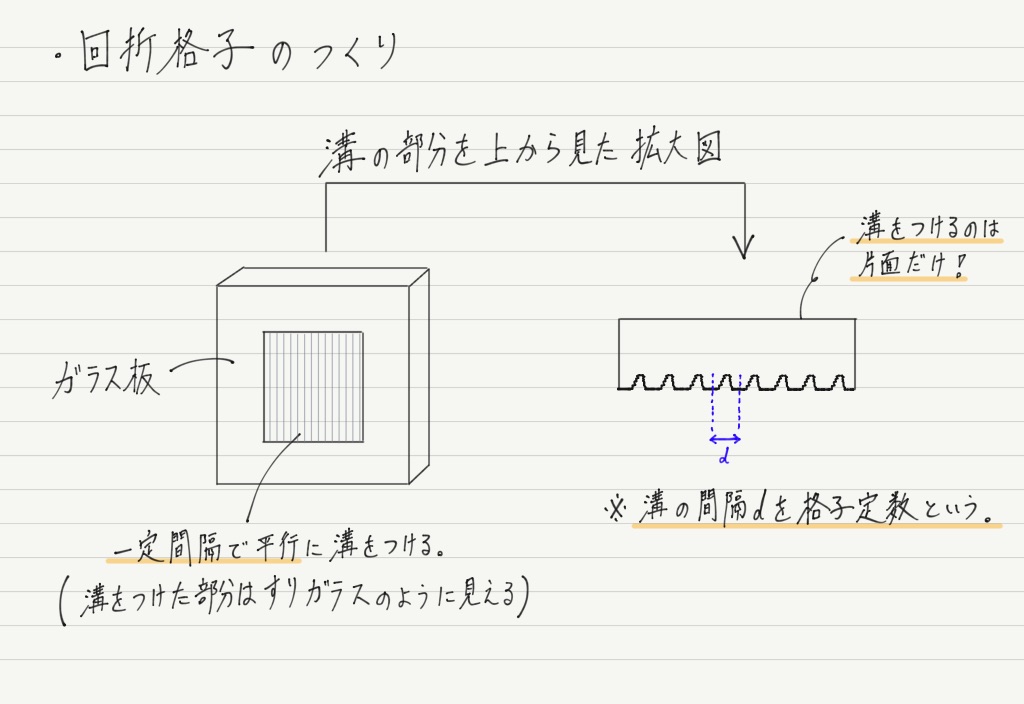
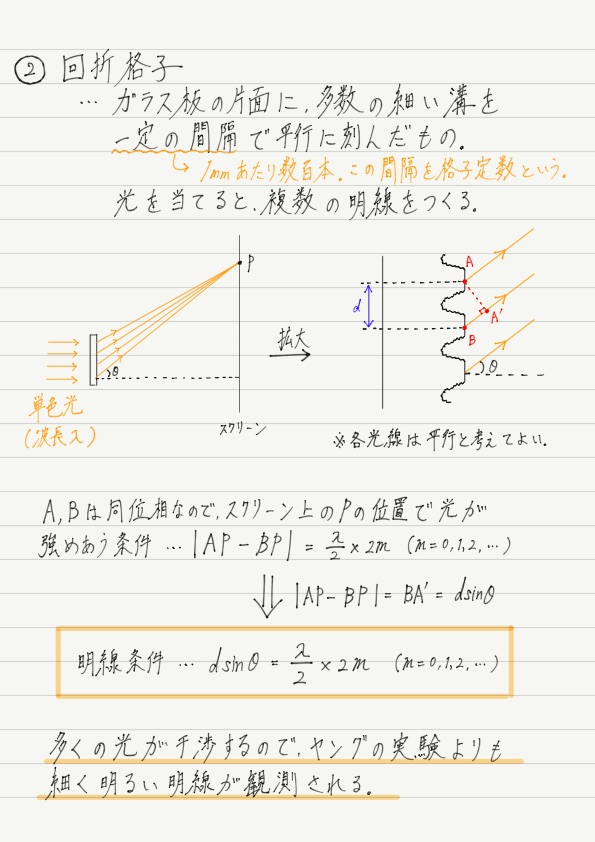
「回折格子」は聞き慣れない名前ですが,簡単にいえばガラスの片面を引っ掻いて溝をつけたもののことです。
正確には,
① 溝は1本や2本ではなく,多数ついている。
② 溝はすべて平行。
③ 溝の間隔は一定で,非常に狭い(1mmあたり数百本)。
という条件がつくので,適当にガラスを引っ掻くだけでは作れません。
この回折格子に光を入射すると,スクリーン上に明線が現れます!
これは一体どういうことでしょうか?
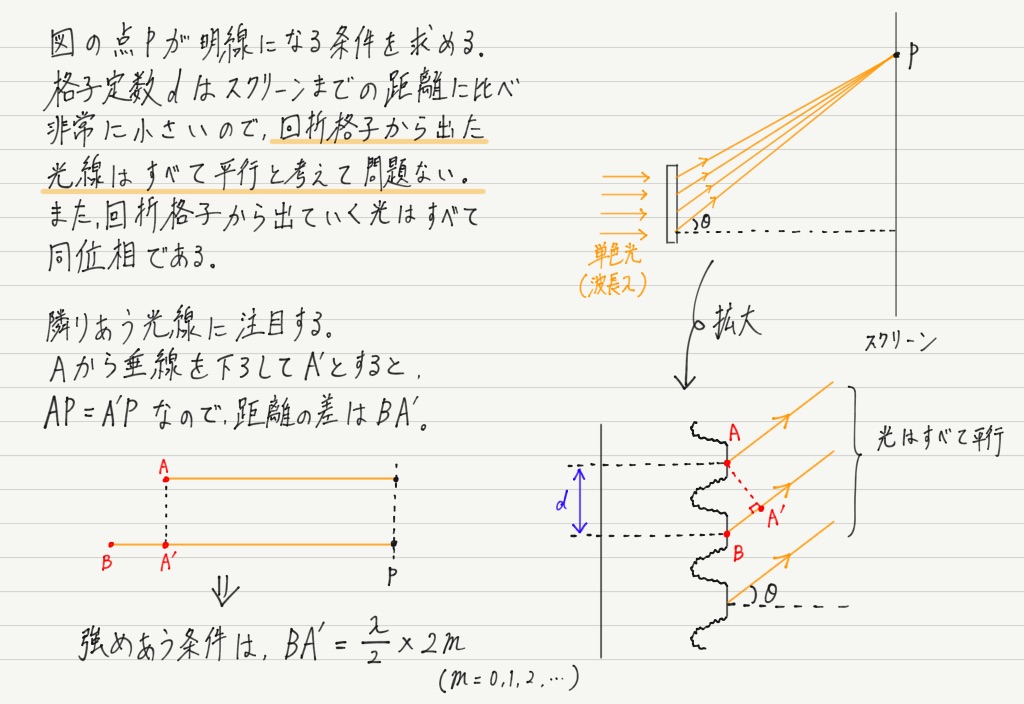
回折格子の明線条件
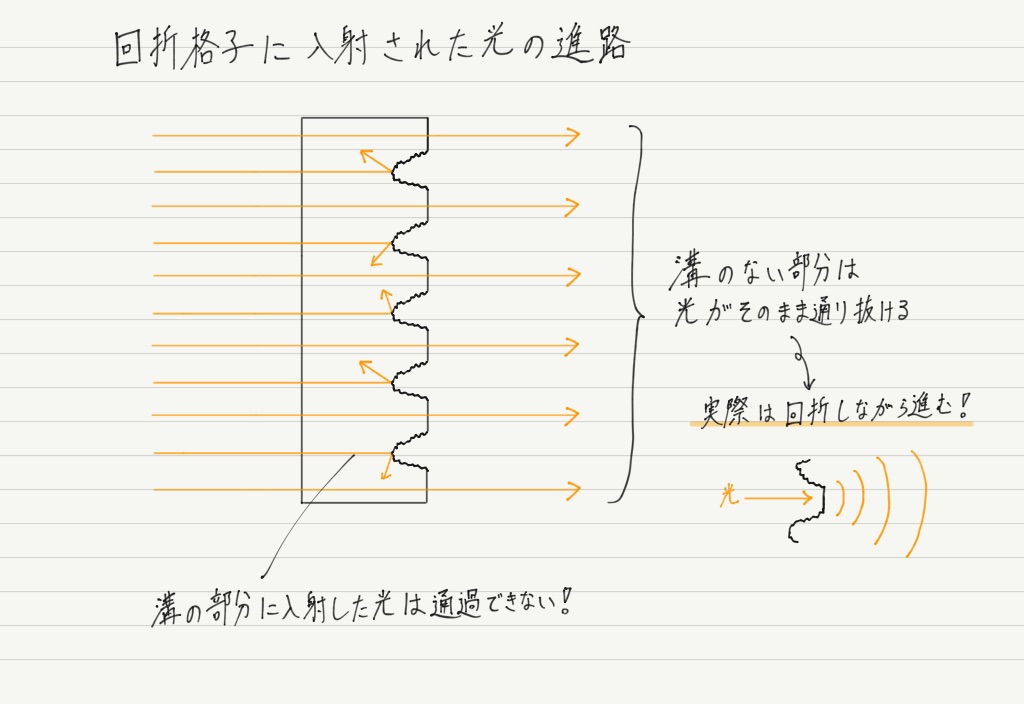
回折格子に入射した光が辿る道筋を見てみましょう。
お分かりですか?
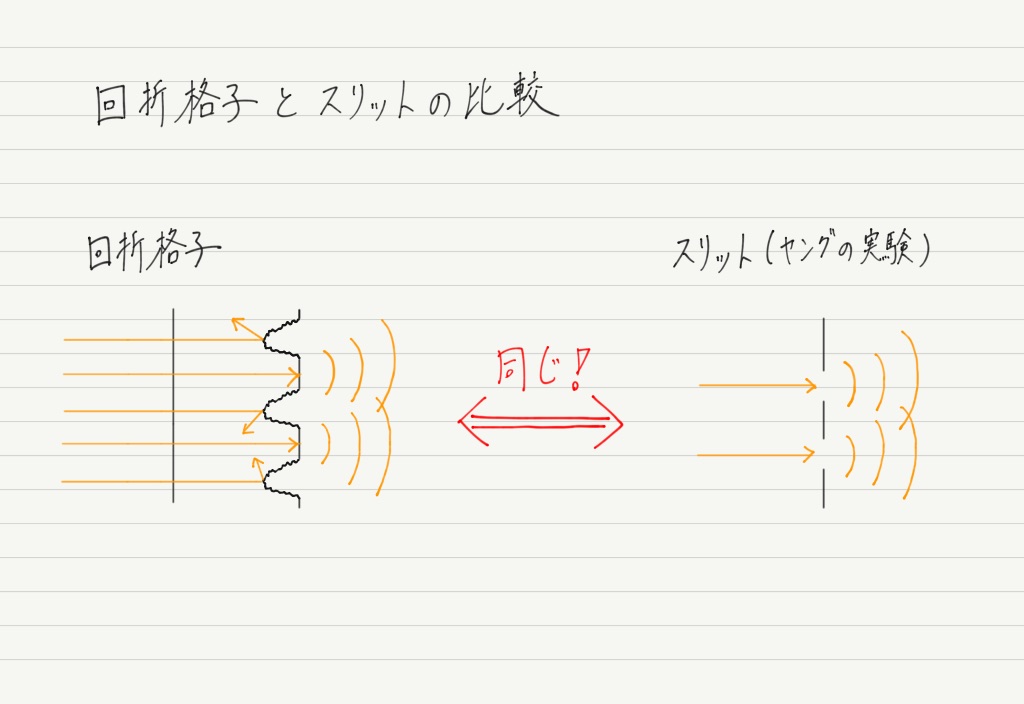
光が通過し回折する部分と遮られる部分があるということは,回折格子はスリットと同じ役割を果たしていることになります!
そうと分かれば,明線条件も求められそうな予感。
ただし,ヤングの実験がスリット2つに対して,回折格子のスリット(に相当する部分)はもっとたくさんあるので,「すべての光が強めあう条件」を考えなければいけません。
うーん,ちょっと難しそうですが,とりあえずやってみましょう!
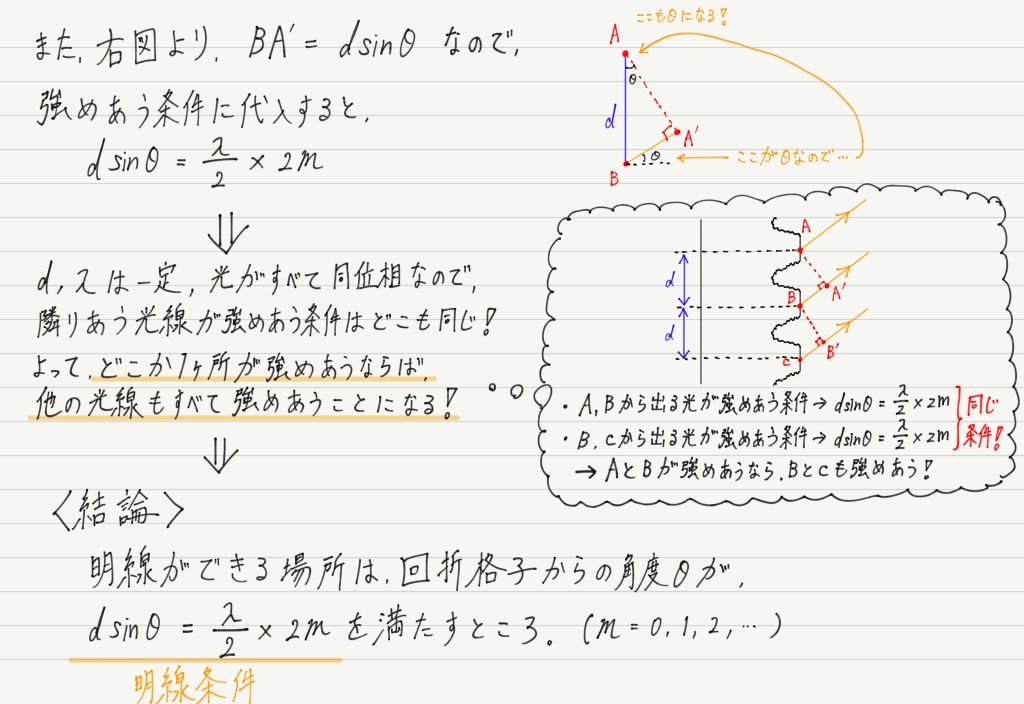
予想に反して,あっさりと明線条件が得られました!
ポイントはもちろん,「隣りあう2つが強めあう条件」と「すべての光が強めあう条件」がイコールになっていること。
回折格子の問題が出たら,小難しく考えずに隣りあう2つの光にだけ注目しましょう!
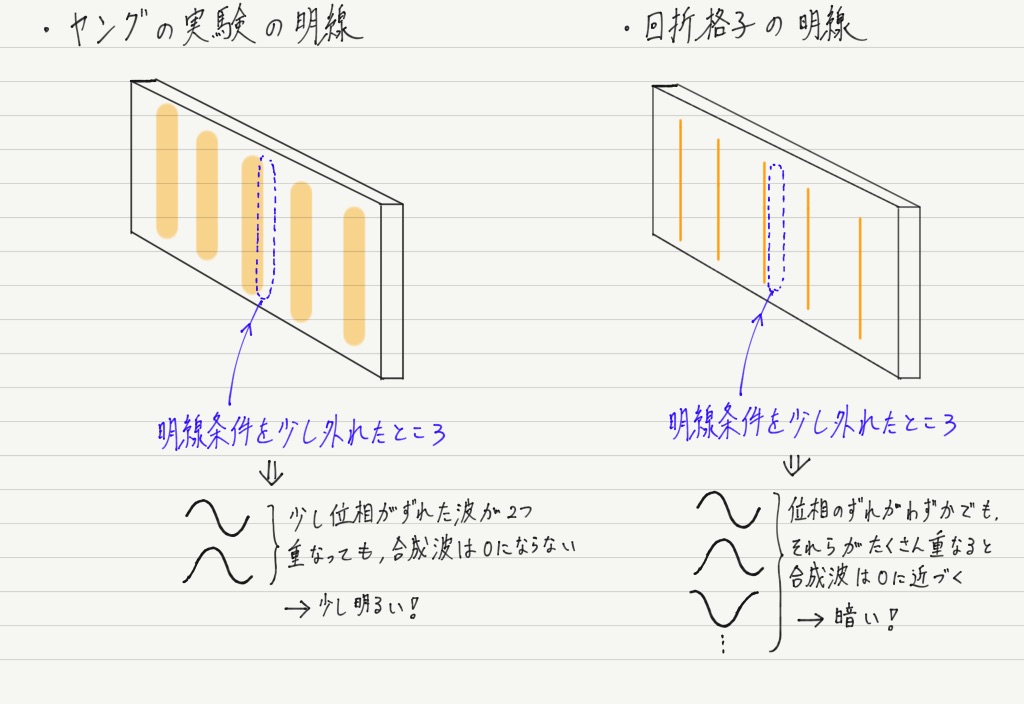
ヤングの実験と回折格子の実験は明線が得られるという意味では非常に似ていますが,明線の見た目はまったく異なります。
結論から言ってしまうと,回折格子の明線はヤングの実験に比べて非常に細く,明るいです!
この差はスリットの数のちがいに由来します。 ヤングの実験ではスリットが2つしかありません。
その2つから出る光が互いに打ち消し合って完全に暗くなるためには,スクリーンでぴったり逆位相になる必要があります(暗線条件)。
裏を返せば,位相がちょっとずれたくらいでは打ち消すことができず,ぼんやり明るいまま。
それに対し,回折格子では光が複数箇所(スリットに相当する部分がたくさんある)から出ます。
光がたくさんあるので,ほんの少しの位相のずれであっても全体では大きな影響を及ぼすのです。
つまり,明線条件をぴったり満たすときは光がたくさん重なるぶん,ヤングの実験のときよりも明るくなるけれど,そこからほんの少しでも外れると途端に暗くなってしまうのです。
今回のまとめノート
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。
次回予告
干渉条件を使った明線条件の求め方は分かってきましたか?
少しずつ応用編に入っていくので,心してかかってください!