前回に引き続き,波の進み方の特徴を見ていきましょう!
反射の法則
まずは反射について。 反射は物理基礎のところでもやりましたね!
物理基礎では反射地点のちがいによる位相の変化,つまり波の “性質” にスポットを当てていましたが,今回はあくまでも波の “進み方” です。
反射板に対して真っ直ぐに入射した場合はそのまま来た道を戻るだけなので,斜めに入射する場合を考えましょう。
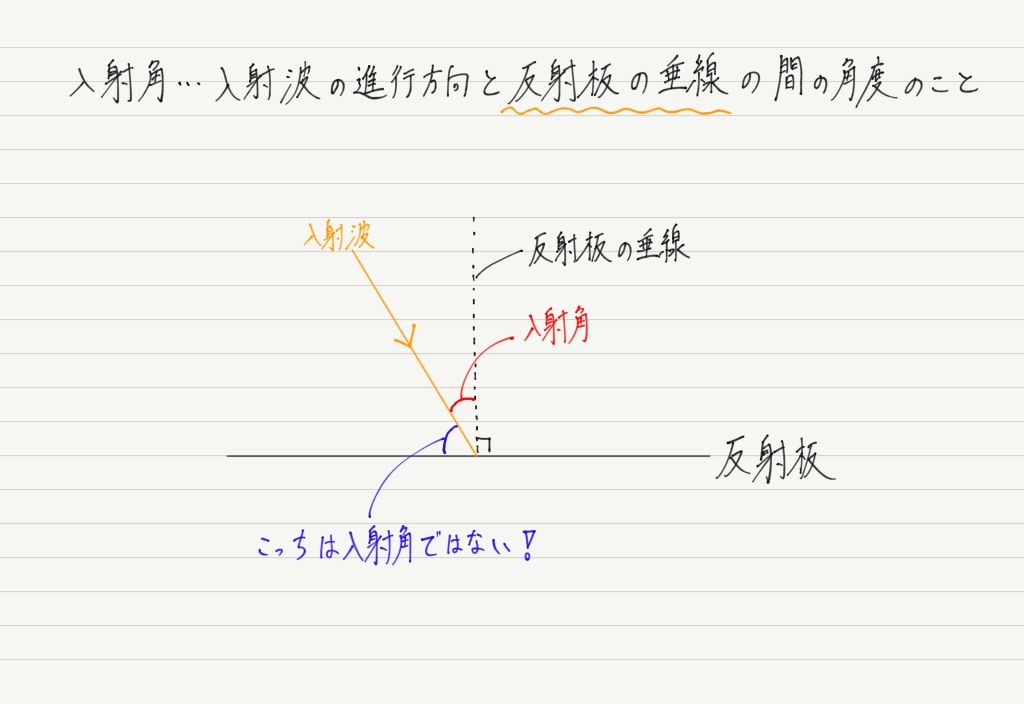
反射板に対し,どれぐらい斜めに入ってくるのかは「入射角」と呼ばれる角度で表します。
慣れていないとどこが入射角か間違えやすいので注意が必要です。
このあと「反射角」や「屈折角」といった角度が登場しますが,それらも入射波同様に,波の進行方向と境界面の垂線の間の角度のことを指します。
では,入射角がθの波はどのようにはね返るでしょうか?
…って,もう知ってますよね(^_^;)
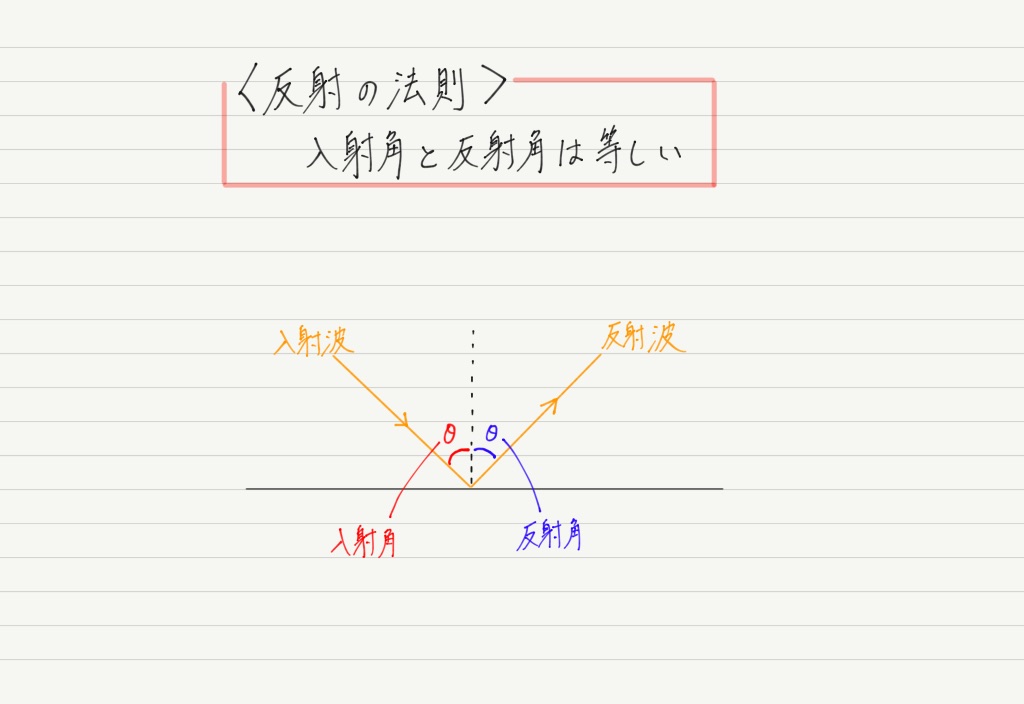
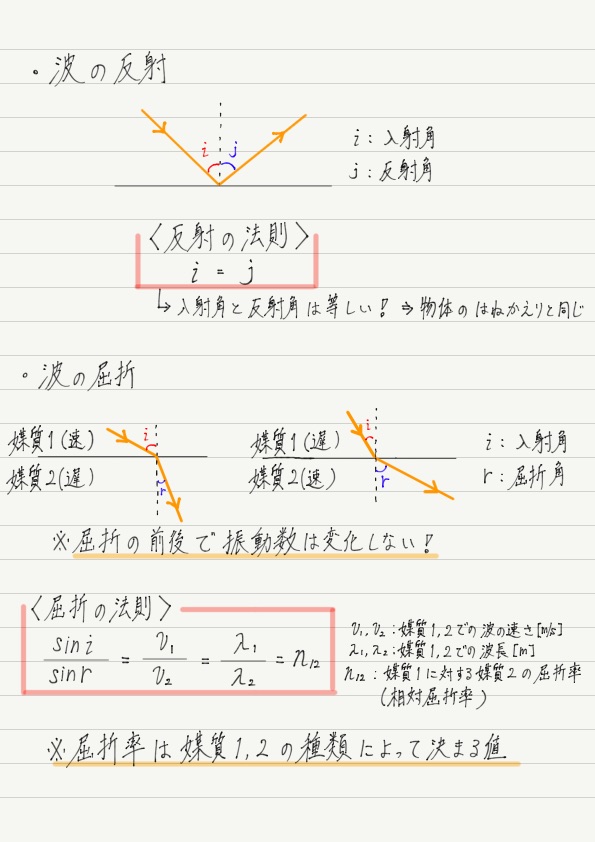
波は入射角と同じ角度ではね返ります。 入射角がθなら,反射角もθです! これを「反射の法則」といいます。
波の運動は物体の運動と異なる点が多いですが,反射に関して言えば壁や床でボールがはね返るときと同じ動きになるということです。
屈折の法則
次に屈折です。 光の屈折については中学校で習うし,音の屈折については物理基礎で触れたので,波が屈折するという現象自体は目新しいものではありません。
しかし,これまでは「屈折=進む向きが変わる」ぐらいのことしかやっておらず,「30°で入射した波はどれぐらい屈折するのか」のような具体的な計算には触れてきませんでした。
今回の目標は,いま挙げたような具体的な問題に答えられるようになることです!
では,その計算を可能にする「屈折の法則」を伝授しましょう。
どっちが分母でどっちが分子だっけ?とならないように,式丸暗記ではなく,必ず図とセットで覚えるようにしましょう。
さて,この法則を見ると,波の速さと波長はそれぞれの媒質で異なるのに,振動数については何も書いてありません。
これはなぜかというと,媒質が変化しても振動数は変わらないからです。
ピンと来ない人はロープを揺らしてできる波で考えてみてください。
振動数とは1秒間にロープを揺らす回数。
つまり,振動数が大きいか小さいかはロープを持っている人(=波源)次第。 ロープ(=媒質)が何でできているかは関係ないのです。
屈折が起こる理由
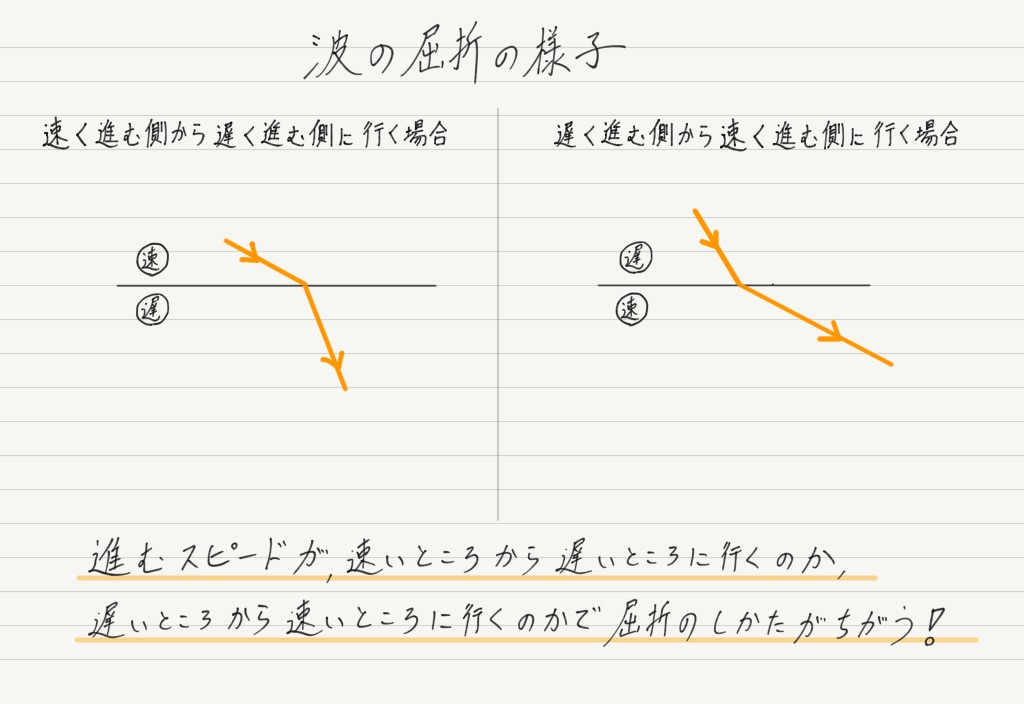
「波の屈折が起こる原因は波の進む速さのちがいにある」と物理基礎の音のところで説明したのを覚えていますか?
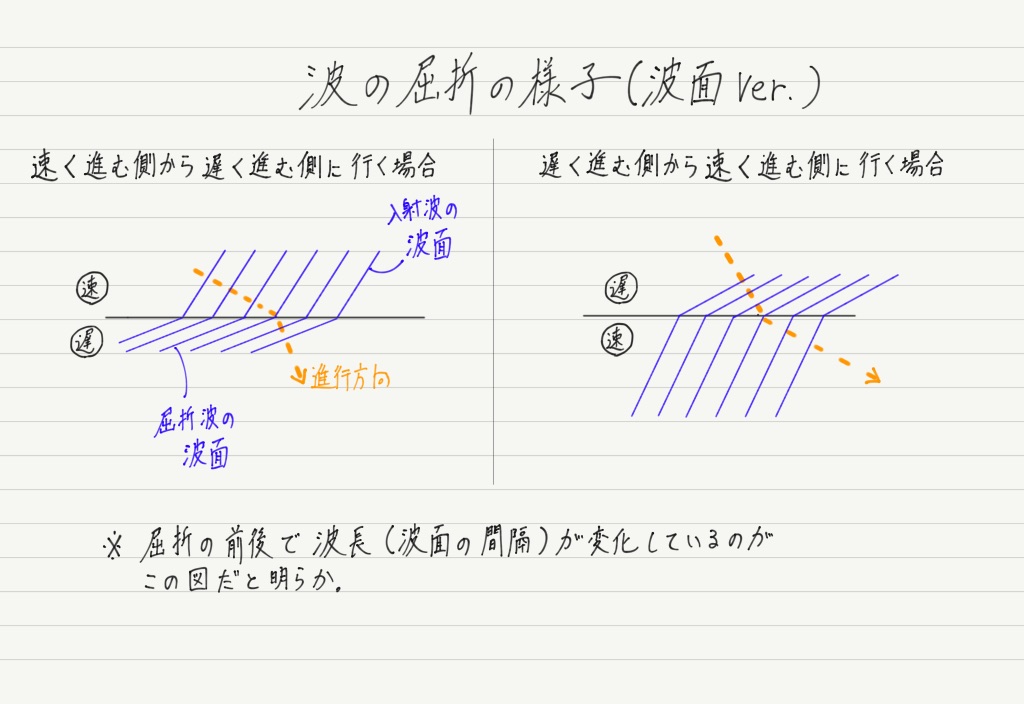
図でわかるように,速い方から遅い方に入射するのと,遅い方から速い方に入射するのとでは曲がり方が逆ですが,正しいイメージが作れれば丸暗記しなくて済みます。
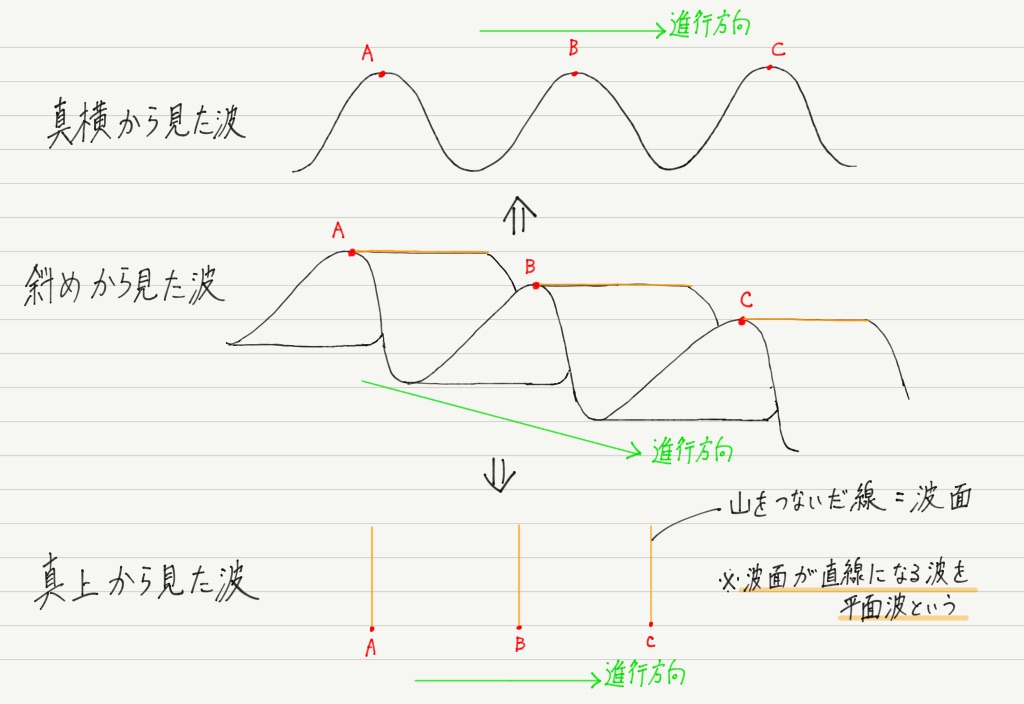
イメージのためには,波を波面を用いて表しましょう。
波面とは,位相が等しい点(例えば波の山の部分や谷の部分)を線でつないだものです。
波面は波を真横ではなく,真上から見た様子を表すときに役立ちます。
(真横から見ればいつもの正弦波!)
トイレットペーパーのような長い帯が波打つところを想像すると分かりやすいです(下図参照)。
この図から,波の進行方向と波面が必ず垂直になることも分かります。
それを踏まえた上で,先ほどの屈折を波面で書き直すとこんな感じになります↓
では,なぜこのように屈折するのかを説明しましょう。
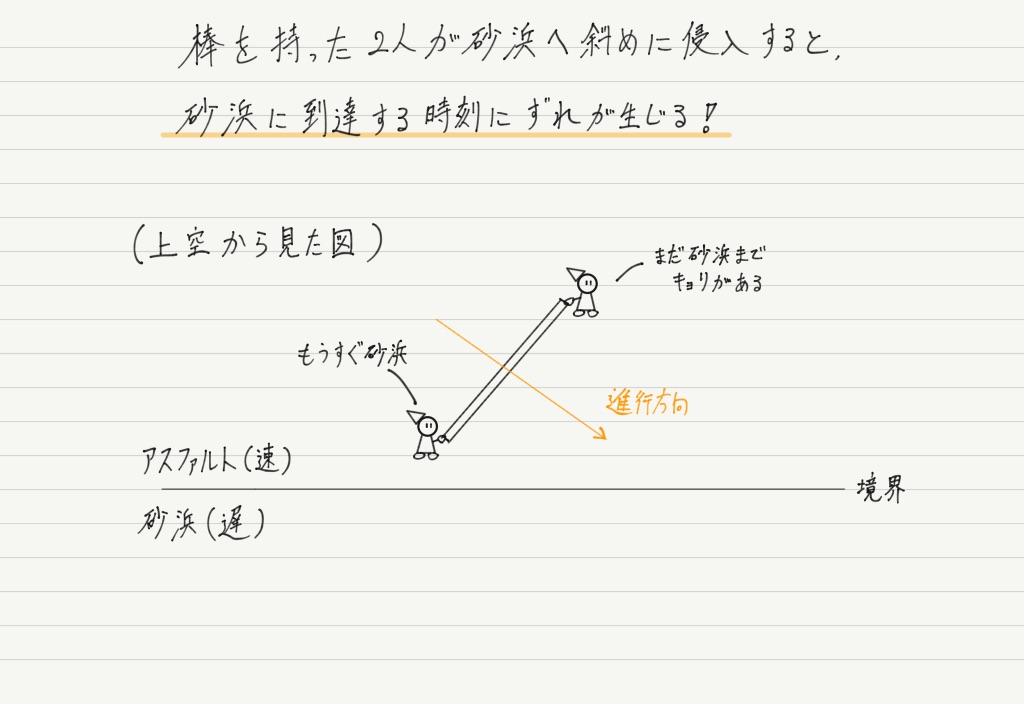
同じ足の速さの2人が長い棒の両端を持って,アスファルトの道路から砂浜に侵入する様子をイメージしてください。
この棒を持った2人がアスファルトから砂浜に向かって斜めに進んでいくと,まず1人が先に砂浜に侵入します。
このとき,アスファルトに比べて砂浜は足が取られるので,砂浜に入った人の進みが遅くなります。
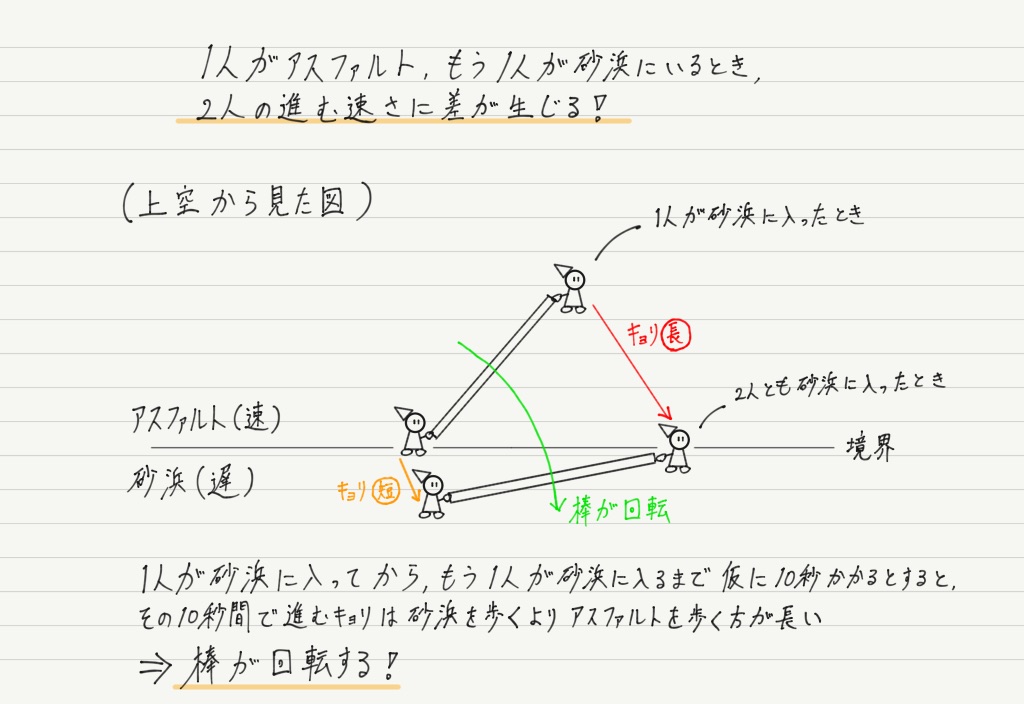
この「1人は砂浜(進みが遅い),もう1人はアスファルト(進みが速い)」という状況こそが波が屈折する理由です。
なぜなら,砂浜に入った方がモタモタ進んでいる間に,アスファルトにいる方はこれまでと変わらぬ速さで進むので,結果として棒が少し回転します!
2人とも砂浜に突入した後は,2人の足並みはまた揃うことになります。
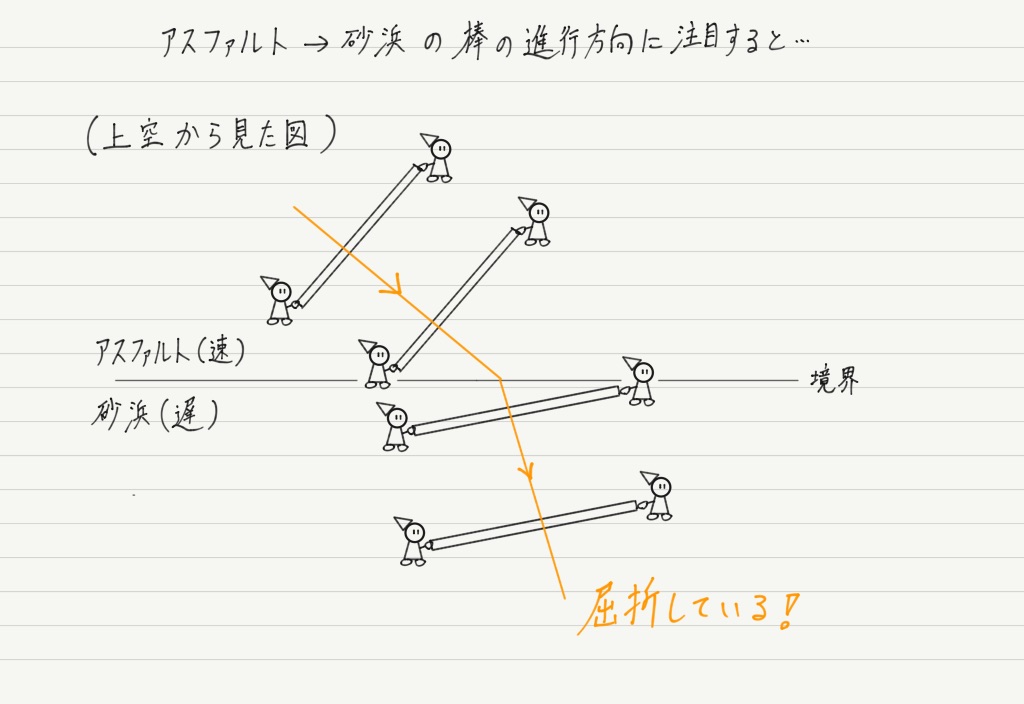
では最初から棒の動きを追ってみましょう。
たしかに屈折して進んでいることが分かりますね!
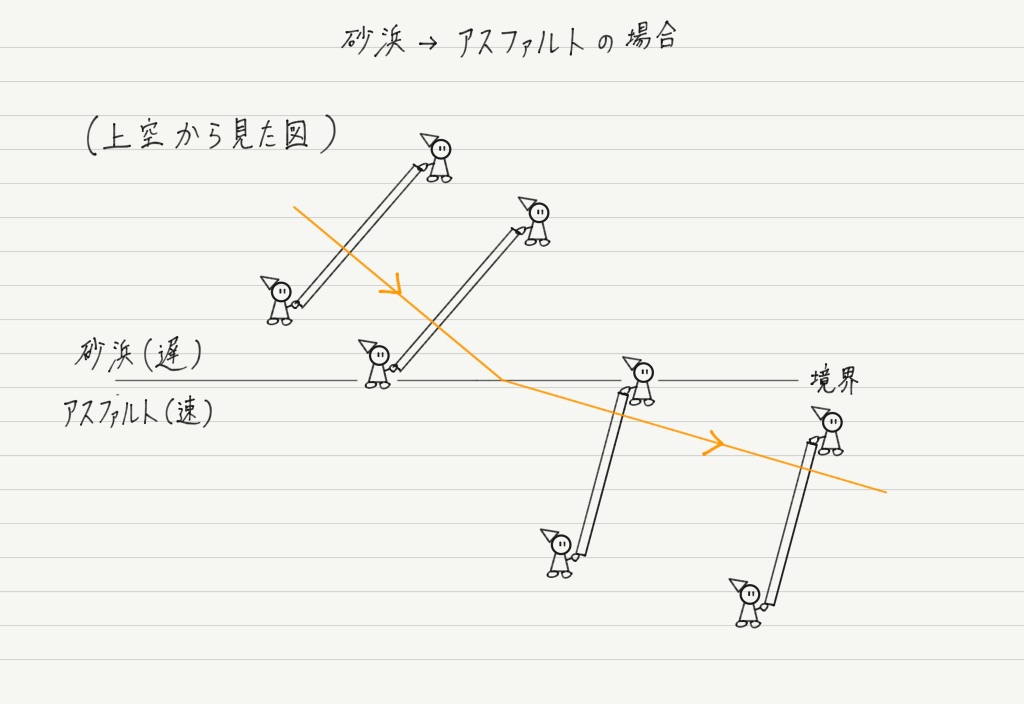
同じ要領で,さっきと逆に,砂浜からアスファルトに侵入する場合も考えてみましょう。
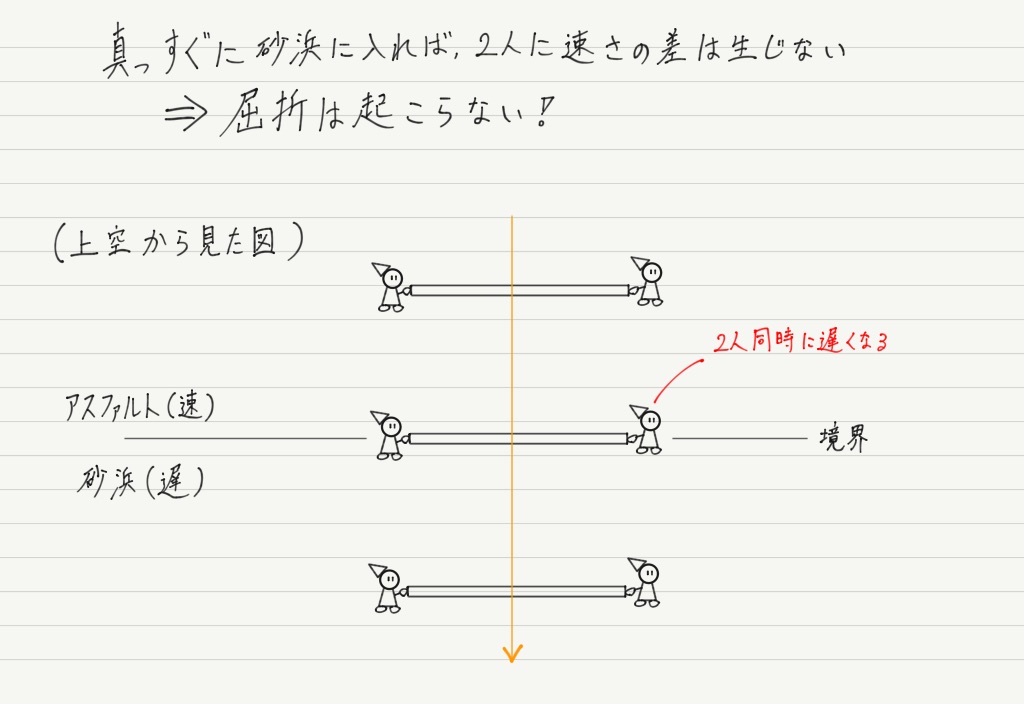
このイメージを使えば,入射角が0°のとき屈折が起こらないことも理解できます。
もうお気付きだと思いますが,この棒は波面を表しています。
よって,いまのイメージから波の話に戻るには,棒→波面,アスファルト→速く進む媒質,砂浜→遅く進む媒質に置き換えればOK!
このイメージさえあれば,波の屈折が起こる理由も,屈折する方向もバッチリ答えられると思います!!
今回のまとめノート
読んでくれた人の中には,「屈折の法則の中にsinが出てくるのはなぜ? cosでもtanでもなく,なぜsin?」と思った人もいると思いますが,その説明は補講に回したいと思います。
でも,とりあえずは屈折の法則を使ってしっかり計算できるようになることが先決。
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。
次回予告
波どうしはぶつかると重なりあいます。
山どうしが重なって大きく振動する点や,山と谷が重なって振動しない点が出てきますが,そのような点の出現には規則性が存在します。
次回はその規則を学びましょう。