物理基礎の波はバッチリですか? 不安がある人は一通り復習してから先に進みましょう。
物理の波分野は物理基礎よりも計算が多く,苦手にしている人が多いです。
基本を大事に,イチからじっくり勉強していくことが大切。
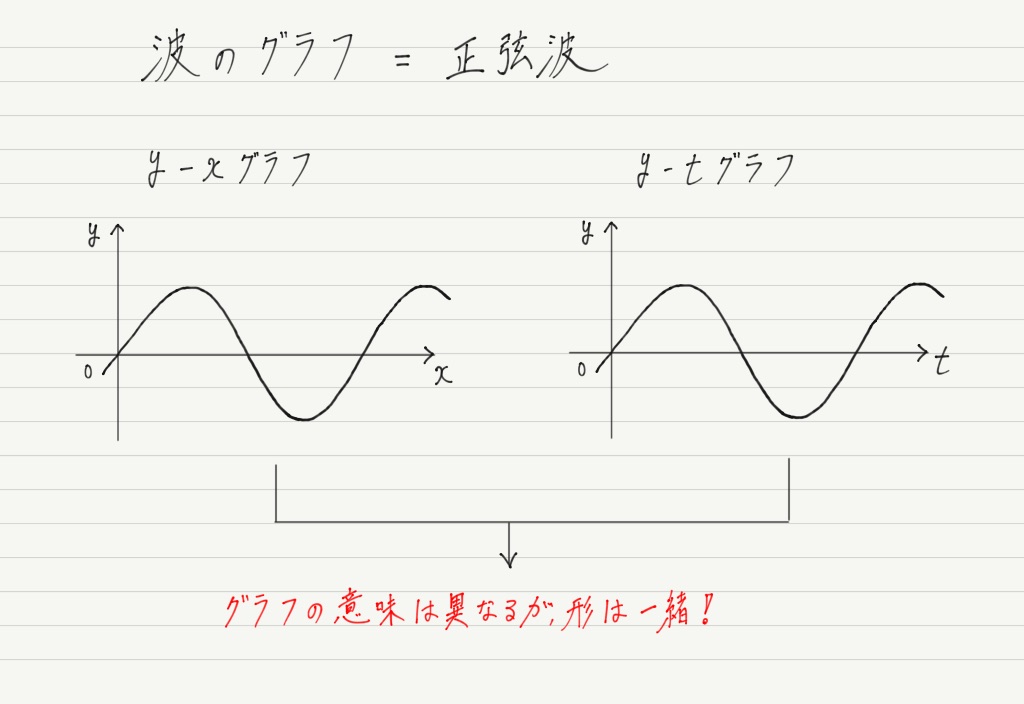
さて,物理基礎では波のグラフを学びました。 具体的には,y-xグラフ,y-tグラフ,縦波のグラフを見てきましたが,大事なのはグラフの概形。 どれも正弦波と呼ばれる形をしていましたね!
数学ではまず「関数」があって,それを「グラフに描く」という手順を踏むわけですが,波では最初にグラフをやってしまいました(^o^;
順序が逆になってしまいましたが,今回は波のグラフを関数で表してみましょう!
媒質の動き=等速円運動と同じ!?
関数で表すということは,最終的な目標は「y=〇〇」という式を導くことです。 波は波源の振動が伝わって起こる現象なので,まずは波源の動きに注目してみましょう。
(※すでに力学で単振動を勉強済みの人は,この部分は飛ばして構いません。 まだ習っていない人用に書いていきます。)
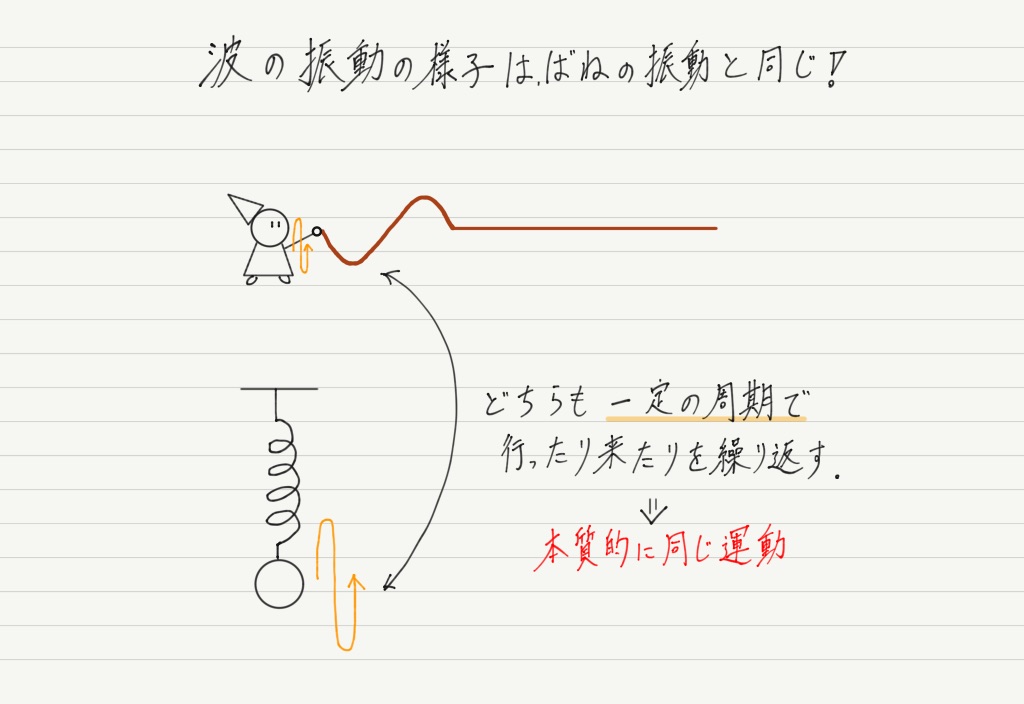
波源の振動は周期的な運動であり,これはばねにおもりを付けて振動させたときと同じ動き(単振動)になります。
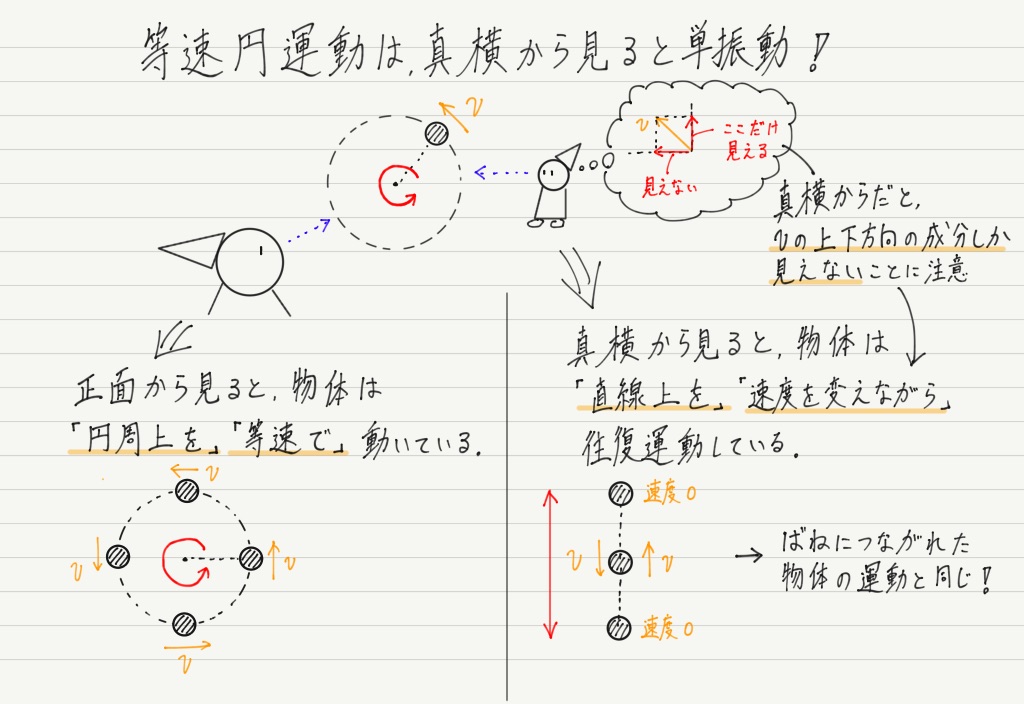
さらに,ばねの振動の様子は,円周上を一定の速さでぐるぐる回る運動(等速円運動)を真横から見たものと同じになることが知られています!!
真横から見ると奥行きがわからなくなるというのがミソ!
10円玉を真横から見ると細長い長方形に見えますよね? それと同じ考え方です。
このことから,振動の様子を調べるためには等速円運動を調べればいいことが分かります。
ばねの振動は位置によって速さが異なるので直接調べるのは難しいですが,等速円運動なら一定の速さなので,運動が調べやすいです。
三角比を用いて振動を表す
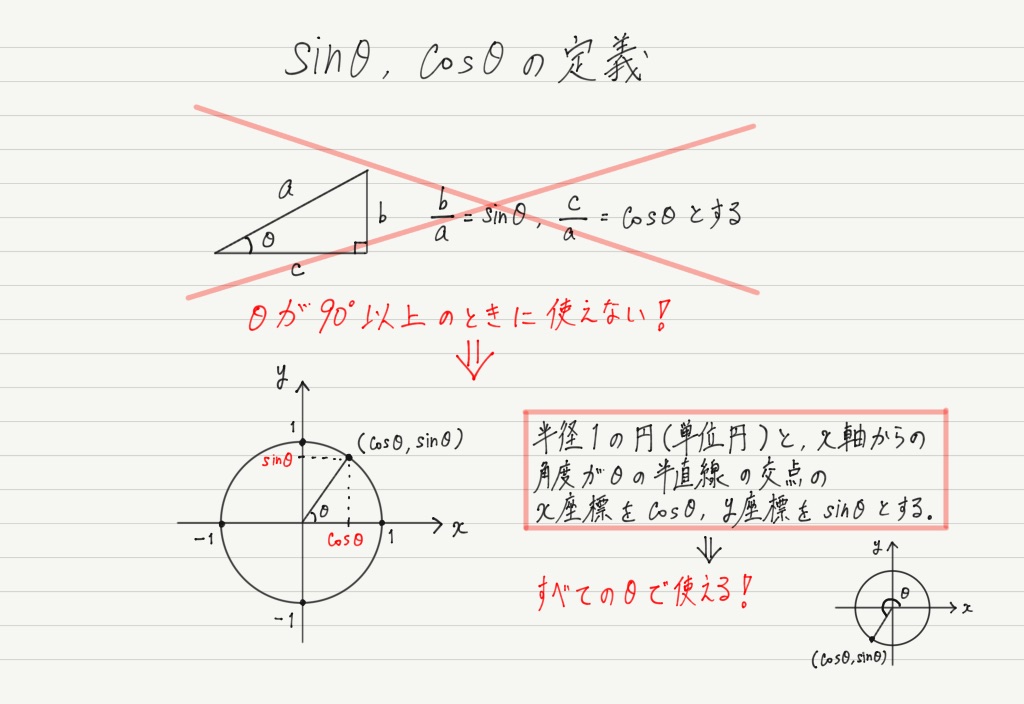
ここで突然ですが三角比の復習です! sinθとcosθの定義を言えますか?
数学では最初,直角三角形を用いて三角比を習います(数学Ⅰ)が, 実際はこの図のように,円を用いて定義されます(数学Ⅱ)。
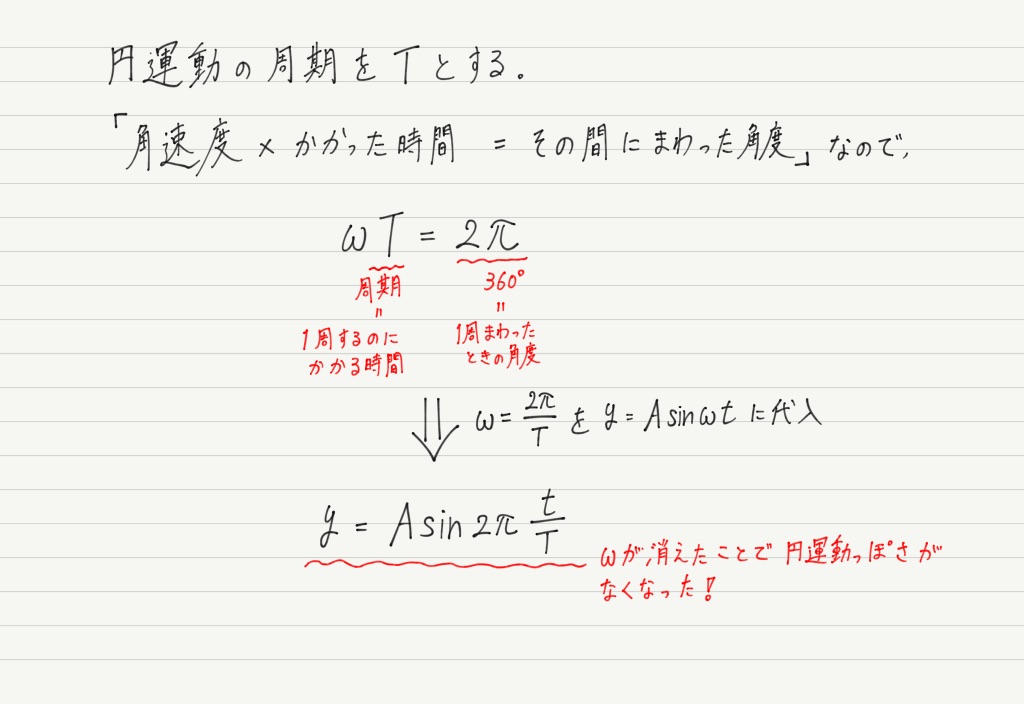
これを用いると,物体が運動を始めてからt秒後のy座標は以下のようになります。
物体が円周上を1周するのにかかる時間をT(周期という)とすると,先ほどの式はさらに式変形できて,
となります。 これが波源(x=0)における振動の関数です。
sinは日本語で正弦。 波形が「正弦波」と呼ばれる理由がこれでハッキリしましたね!!
原点以外の媒質の振動はどう表せるか
今回の我々の目標は,「時刻tにおける,ある場所xでの波の変位」を関数で表すことですが,まだ「時刻tにおける,x=0での波の変位」しか求められていません。
しかしここまでくれば,あとはたった1つのアイデアだけで,目的の関数にたどり着けます。
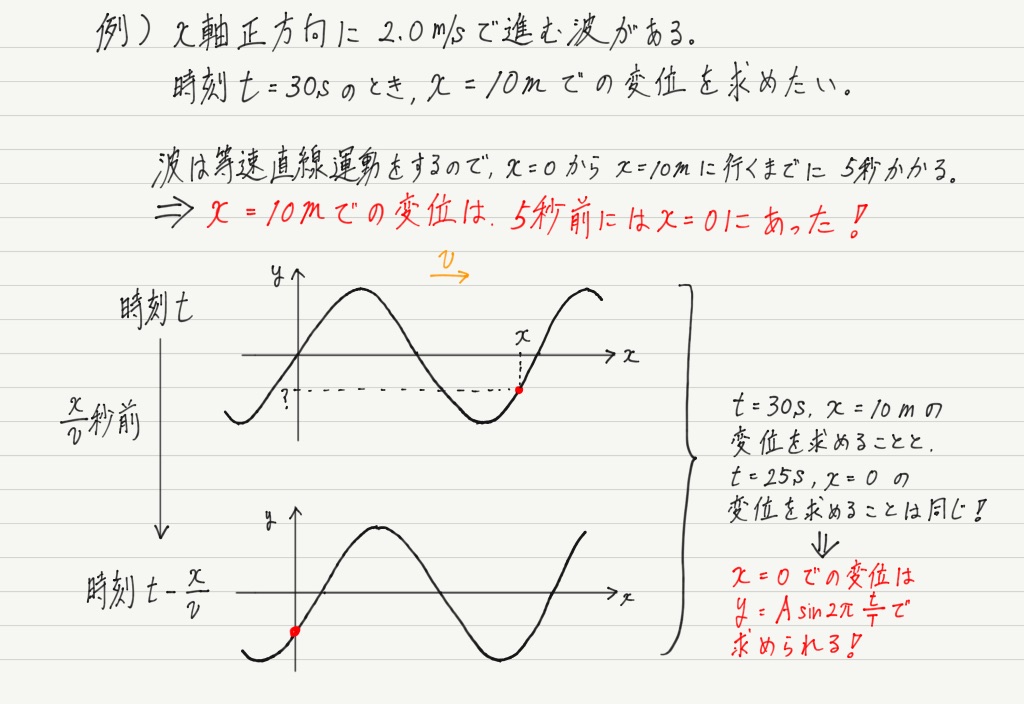
そのアイデアを得るために,「波は等速で進む」という事実を思い出しましょう。 波とは,媒質に波源(x=0)の振動が伝わることで生じます。
もうわかりましたか? 波の関数を得るためのアイデアとは,「媒質の振動を,波源の振動で置き換えること」です!!
…これだけじゃ言葉足らずなので例を出しましょう。
このように,目的のx座標まで波がやってくるのにかかる時間を計算し(等速直線運動なので簡単に求められる),その時間だけ巻き戻した時刻での波源の変位を求めれば万事解決です!!
式の導出はまとめノートに記しておきましょう。
今回のまとめノート
位相について
まとめノートにもう書いてしまいましたが,正弦波の式のsinの “中身(=角度にあたる部分)” のことを位相といいます。 物理基礎のときは軽くしか説明できませんでしたが,やっと説明できた…!
以前は「位相とは媒質の振動の状態を表す量である」と説明していましたが,sinの中身によって,振動の状態が確定することを考えれば,あながち間違いではないでしょう。
ところで,本によっては「逆位相」のことを「位相がπずれている」と表現することがありますが,この表現も“角度”を念頭に置いたものです。
角度は360°(=2π)ずれたら元に戻るのだから,180°(=π)だけずれたら真逆になるのは当たり前。
物理基礎の知識だけだと「π?何のこっちゃ?」となるのですが,位相=角度と考えれば理解できますよね!
ここまで理解できた方は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。
次回予告
波には普通の物体の運動にはない様々な性質があり,そのいくつか(独立性,重ね合わせなど)は物理基礎で扱いました。
が,すべてを紹介できたわけではありません。 次回から数回にわたって,物理基礎で扱わなかった波の性質について見ていきます。