ギターの弦を指ではじくと音が鳴ります。
弦の張りを強くしたり弱くしたり,または弦を指で押さえたりして音程を変えられますが,そういう操作をせずに弦を1本はじくだけなら,プロのギタリストがはじいても,素人がはじいても同じ音が出ます。 その人の技量や力の強弱に関係なく常に同じ音。
そう,前回やった固有振動が弦に生じているのです! 今回はこの弦に生じる固有振動について調べてみましょう。
弦の固有振動はどんな振動か
弦の真ん中あたりをはじくと,その場所が波源となって振動が弦の端へ伝わります。
ギターの弦は両端が固定されているので,端に到達した波は固定端反射をして逆向きに進みます。 その結果,端に向かって進む波と反射して戻ってきた波が重なりあって,弦には定常波が生じることになります!
弦の固有振動の正体はこの定常波に他なりません。 定常波を忘れている人は復習しましょうね!
この弦にできる定常波ですが,ひとつだけ制限があります。 それは弦の両端が固定されていること。
固定されていたら振動できないので,弦の端は必ず定常波の節になります!
弦の固有振動の種類
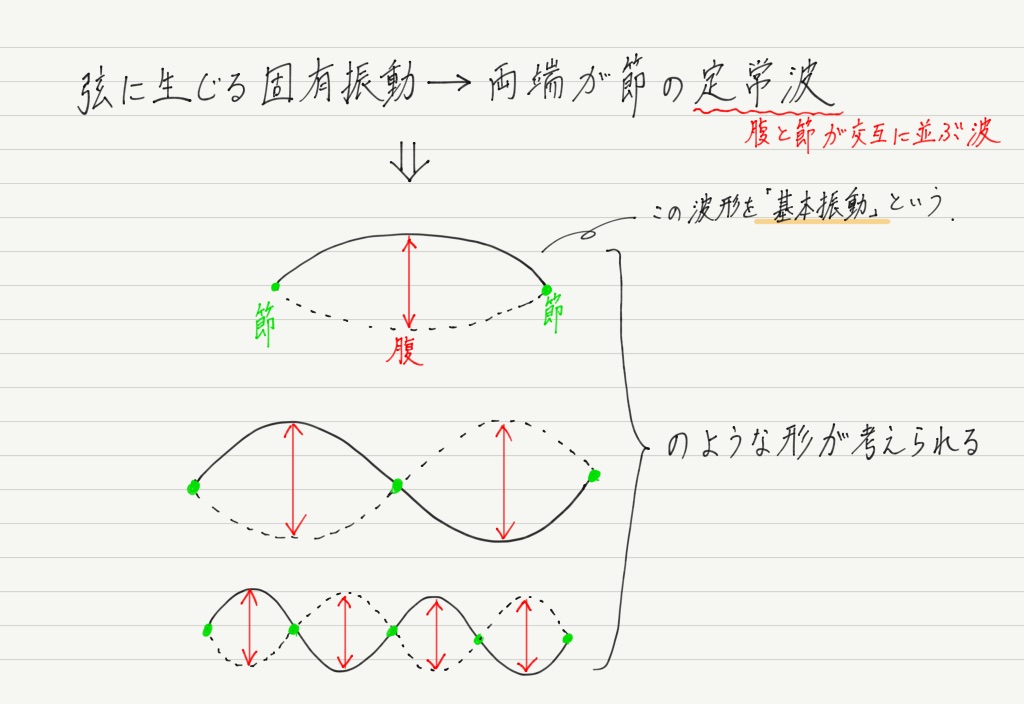
弦の固有振動=両端が節の定常波であることがわかったので,理解を深めるために具体的に図を書いてみましょう。
定常波は必ず腹と節が交互に等間隔で並ぶことに注意すると,弦に生じる固有振動には複数のパターンが考えられます。
このように複数の振動が考えられる中で,一番シンプルな形の定常波を基本振動と呼びます。
今回の場合は腹が1つだけの定常波が基本振動。
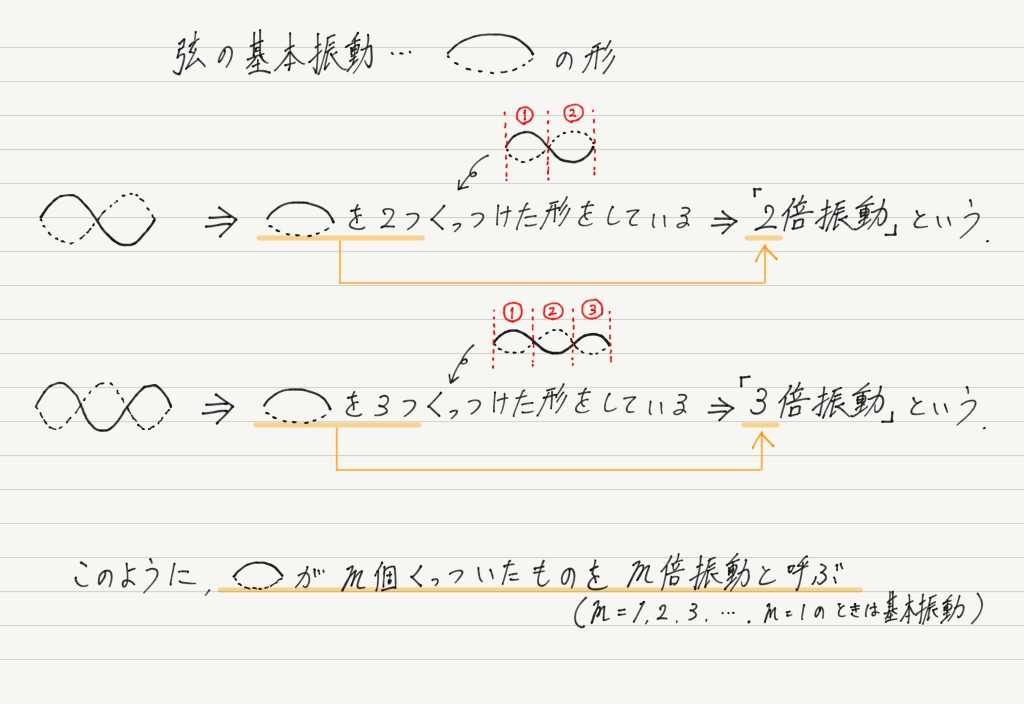
その他の定常波は基本振動の形を何個かくっつけたような形になっているので,基本振動の形が何個分くっついているかで区別します。
弦楽器では,弦にこれらの振動が生じ,混ざりあって音を奏でています。
弦の固有振動の考察
実際に弦にこれらの振動が生じているとき,どのような音に聞こえるか(固有振動数)を求めてみましょう!
弦の長さをL[m]として,まずは基本振動と2倍,3倍振動の場合について考えてみます。
このようにして,弦の長さと波長の関係式が得られます。
そして,波長が分かれば波の基本式を用いて振動数を求めることが可能です!
これが基本振動,2倍振動,3倍振動の固有振動数。
2倍振動の振動数は基本振動の2倍,3倍振動の振動数は基本振動の3倍になっています。 4倍振動以降もそのようになっているのでしょうか?
4倍,5倍,…とやっていてもキリがないので,ひとまとめにしてやってしまいましょう!
1,2,3の場合をそのまま拡張していきます。
これがm 倍振動の固有振動数で,確かに基本振動のm 倍であることがわかります。
この結果は丸暗記してはダメです! どうやってこの式を求めたか,その過程も含めて理解しておく必要があります。 自分で固有振動数の式が出せるようになるまで何回でも読み返してください。
固有振動数からみる弦楽器のしくみ
せっかく弦の固有振動数の式が得られたので,もう少し詳しく見てみましょう。
まず,vが分子に乗っているので,固有振動数が弦を伝わる波の速さに比例することが分かります。 vは弦の張力や,(1mあたりの)質量に関係しています。
弦楽器の音程を合わせるとき,弦の張りを強めたり弱めたりしますが,あれは張力で波の速さをコントロールしているのです。
また,弦の質量が大きいほどゆったりした振動となり,波の伝わる速さが遅くなります。 ギターに太い弦と細い弦があるのは,弦によって音階を変えるのに質量を変える必要があるからです。
次に弦の長さ。 Lが分母にあるので,固有振動数が弦の長さに反比例していることが分かります。 つまり弦が長いほうが振動数は小さく,音が低くなる。 そういえばベースはギターよりも弦が長いですよね!
逆に弦を短くすれば音が高くなるのですが,弦楽器の演奏はこの性質を利用しています。
もちろん演奏中に弦を切って短くするわけにはいかないので,そのかわりに弦を指で押さえるわけです。 押さえたところが固定端となって,振動は押さえたところから先には伝わりません。 これで短い弦を弾いているのと同じことになるわけです!
弦楽器の原理についてこれだけのことが固有振動数の式たった1つからわかるというのはすごいですよね!
今回のまとめノート
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。
次回予告
今回は弦楽器だったので,次回は管楽器にスポットを当ててみましょう!