同じ速さ,同じ波長,同じ振幅の2つの波が互いに逆向きに進んできて合成波をつくるとき,定常波とよばれる波ができるのでした。
では,まったく同じではなく,少しずれた波が重なる場合はどうなるでしょうか?
徒競走の例
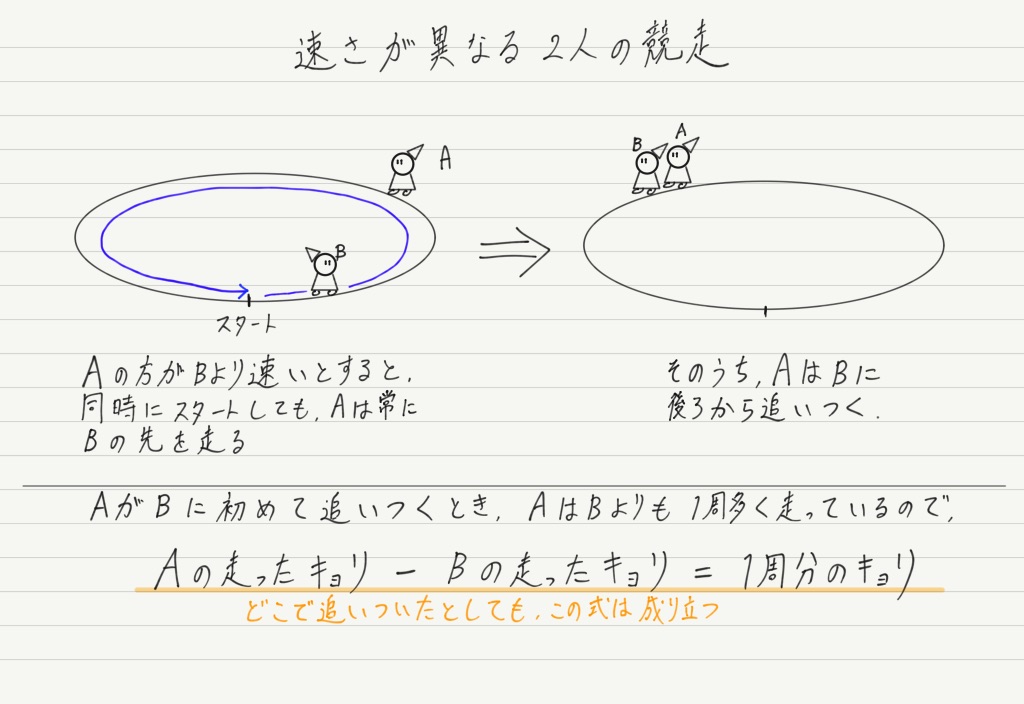
波の話をする前に,まずイメージをもってほしいので,AさんとBさんが陸上競技のトラックを走る場面を想像してください。
2人はそれぞれ一定の速さで走り続けますが,AさんはBさんより速いとしましょう。
同時にスタートするとAさんは常にBさんの前を走ることになりますが,トラックは周回しているので,やがてAさんは遅れて走っているBさんに追いつきます。 いわゆる周回遅れです。
このとき,AさんはBさんよりも1周分多く走っているので,
Aさんの走った距離 − Bさんの走った距離 = トラック1周分
という式が成り立ちます。
ずれた波どうしも周回遅れする
では,いまの話を波に置き換えましょう。
上の例では,2人の “速さ” がずれていましたが,ここで考察したいのは,“振動数” がずれている場合です。
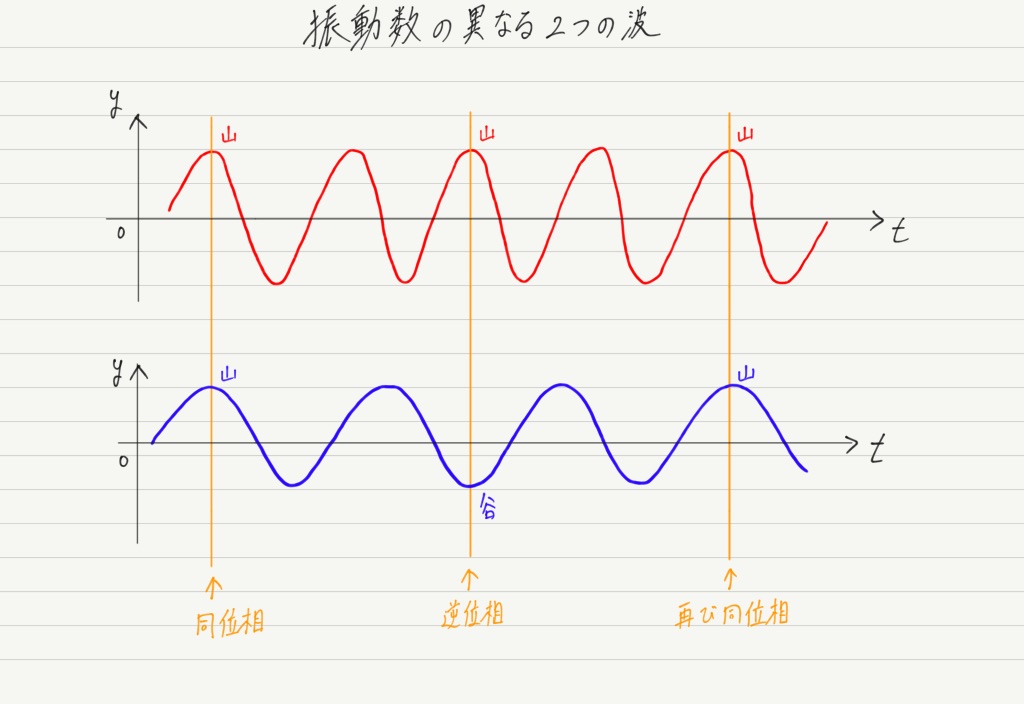
2つの波源から振動数のずれた波を同時に出すことを考えます。
位相が同じところを(図では山どうし)を見つけて,そこから2つの波の様子を追っていきます。
振動数がずれているので時間が経つにつれて徐々に2つの波はずれていきますが,しばらく経つと再び同位相で重なる部分が出てきます。
徒競走の例との類似点に注目してください。 波が周回遅れして,ふたたび同じところが出会ってしまったというわけです。 これが今回扱う現象の大事なポイントになります!
ずれた波どうしの合成
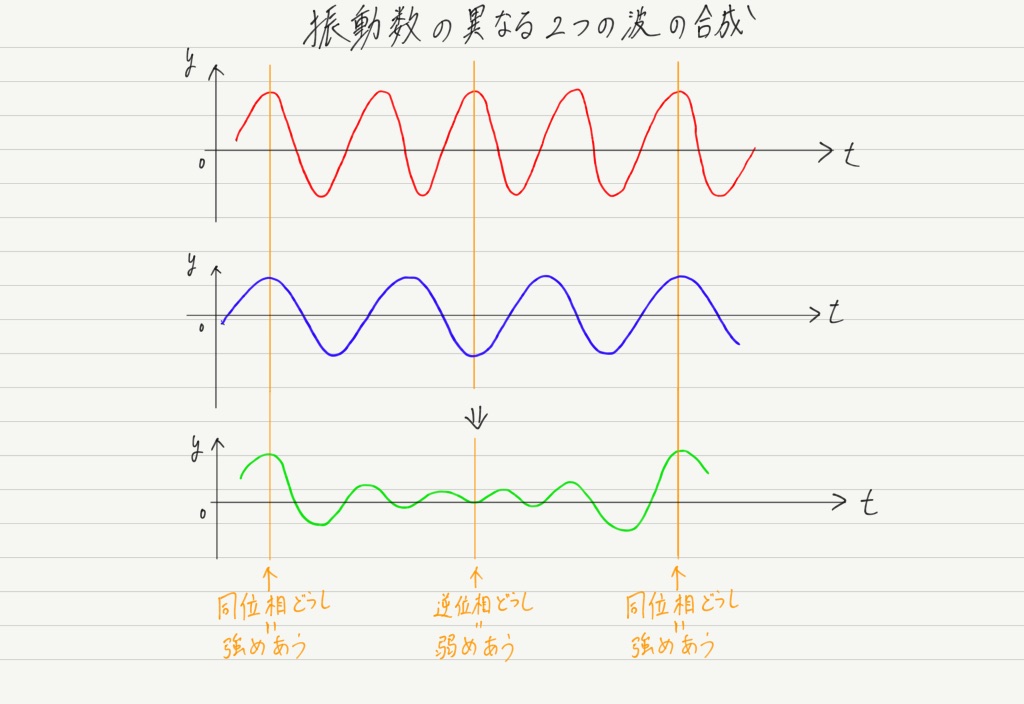
ずれた波どうしを重ねると合成波はどうなるでしょうか?
これはちょっと難しい問題ですが,結論としては
のようになります。
振動数のずれた波を合成すると,振幅が一定ではなく,大きくなったり小さくなったりしながら振動する波ができあがるのです。
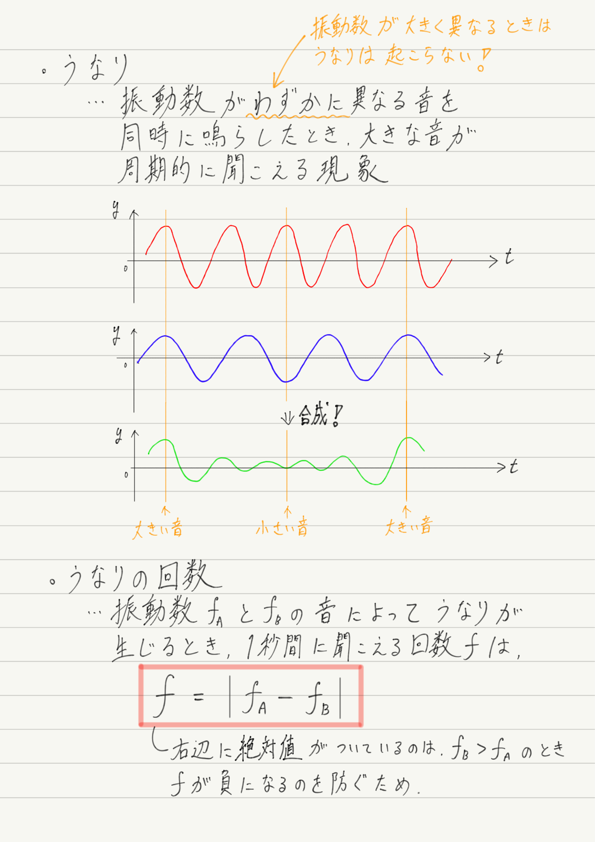
うなりとは
上のグラフが音波を表しているとします。 すると,振幅=音の大きさだったので,振幅が大きくなったり小さくなったりする音は,「… ウォーン … ウォーン … ウォーン …」と,周期的に音が大きく聞こえたり,小さく聞こえたりを繰り返します。
この現象がうなりです。 うなりの音はネットで探せば聞くことができるので,ぜひ一度聞いてみてください。
不快な音です(笑)
うなりの計算
最初に「ウォーン」と聞こえてから,次にもう一度「ウォーン」が聞こえるまでの時間を,うなりの周期といいます。
これを用いると,「うなりの振動数(1秒間にうなりが何回聞こえるか)」を計算で求めることができます!!
計算をここから一歩進めるためのポイントは,ズバリ,周回遅れ。 一番最初にやった徒競走の例を思い出してください。
最初にBさんに追いつくまで,Aさんは1周余計に走っているので,「Aさんの走った距離 − Bさんの走った距離 = トラック1周分」でした。
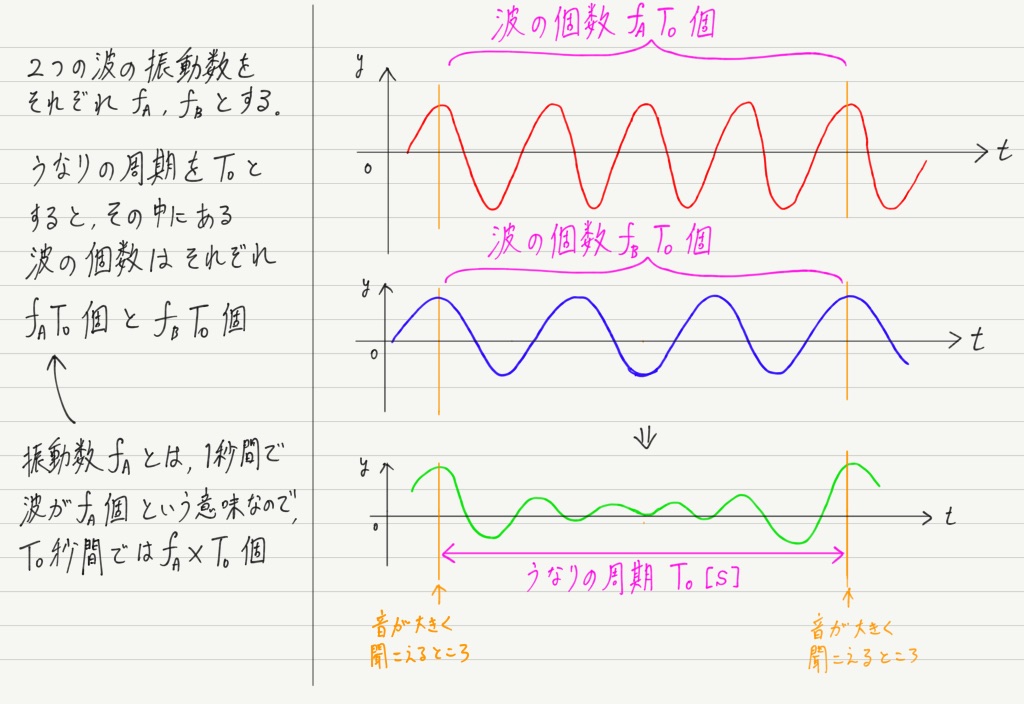
うなりの計算でもこれと同じことが成り立ちます。 うなりで大きな音が聞こえるのは,波が同位相で重なっているときです。
つまり,うなりの周期とは,「同位相で重なった2つの波が,次に同位相になるまでの時間」であると言えます。
振動数の異なる2つの波は次に同位相になるまでに周回遅れするので,徒競走の例と同様に,
Aの出した波の個数 ー Bの出した波の個数 = 波1個分
という式が成り立ちます。 これをまとめると,
1秒間に聞こえるうなりの回数は,もとの波の振動数の差で求められる,という結論が得られました!
現象はやや複雑ですが,それとは裏腹に式はとても簡単です!
うなりの活用
振動数がずれているとうなりが生じることが分かりましたが,これは逆に言えば,うなりが聞こえなければ振動数は合っているということです。 これを利用しているのが楽器の音合わせ(チューニング)。
正しい音階の音源と,チューニングしたい楽器を同時に鳴らします。 このとき振動数が微妙にずれているとうなりが聞こえます。
そこで,うなりを聞きながら音の高さを調整していき,うなりが聞こえなくなったらチューニング完了。 うまい方法だと思いませんか?
今回のまとめノート
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。
次回予告
音の応用として楽器を取り上げたいのですが,次回はその準備として “物体の揺れ方” について見ていきたいと思います!