今回は波を扱う上で非常に大切な式を学びます。 前回と同様,ロープを伝わる波を例に説明しましょう。
波長と波の速さ
まずは復習。 ロープを “1回” 振動させると,“1個” の波ができるのでした。
詳しくは前回の記事参照↓
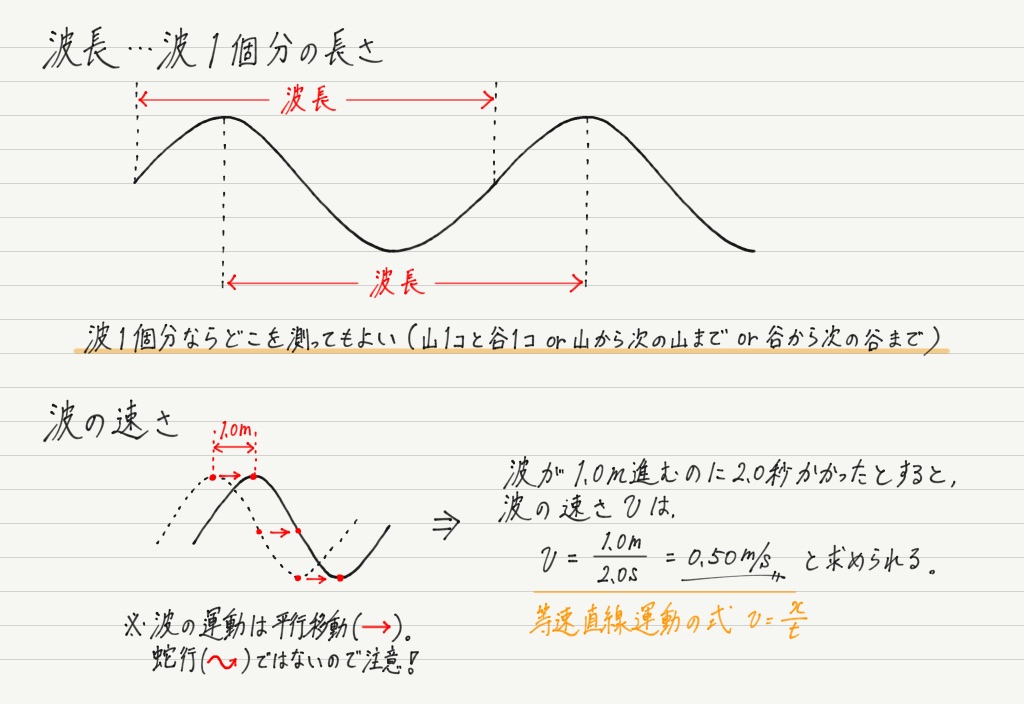
波1個分の長さのことを波長といいます。
また,ロープに生じた波はその場にとどまるわけではなく,手から離れる方向に向かって進んでいきます。
このときの波の進む速さを「波の速さ」といいます。(そのまんま笑)
波の速さは媒質の種類によって決まるので,同じ媒質を進むのであれば波は等速直線運動をします。 つまり,進んだ距離とかかった時間が分かれば,距離÷時間で波の速さを求めることができます。
波の基本式
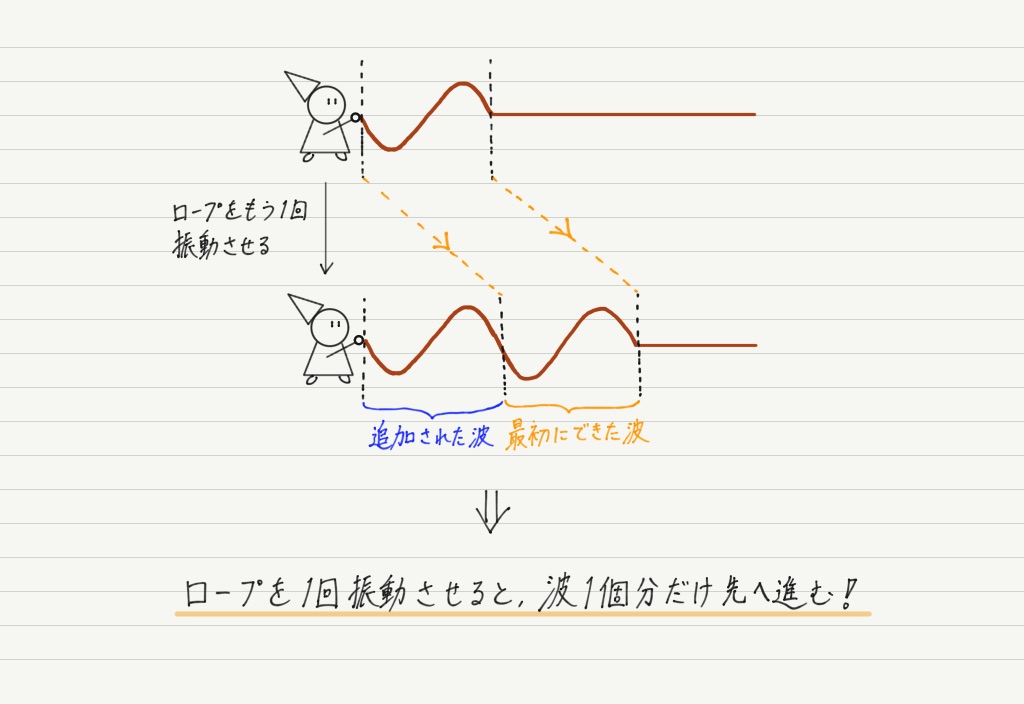
さて,ロープを1回振動させて1個の波をつくった後,続けてもう1個波をつくってみましょう。 このときロープには2個分の波が並ぶことになります。 この並んだ2つの波について考察してみましょう。
上の図の通り,ロープを1回振動させると新しい波が1個発生します。その新しく生じた波が入る場所を確保するため,元々あった波は,波1個分先へ進むことになります。
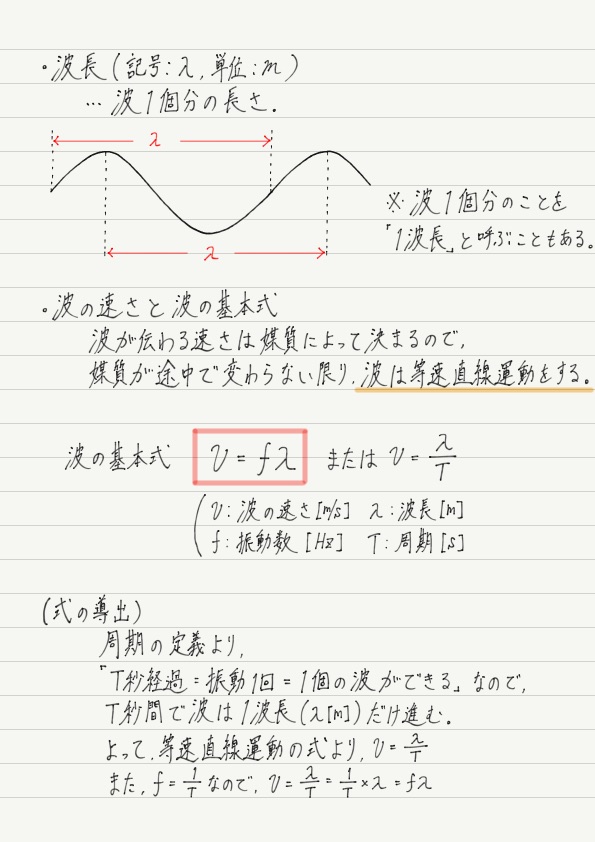
1回の振動にかかる時間=周期 T ,波1個分の長さ=波長 λ なので,上で書いたことを言い換えると,「時間がT[秒]経つと,波はλ[m]だけ進む」となります。
そして,波の速さ=進んだ距離÷かかった時間 なので,波の速さ v[m/s]は,Tとλを用いて, v = λ ÷ T と書くことができます。
さらに前回導出した式,fT =1を使って T を消去すると,v = fλ と書くこともできます。 この式は波の分野では非常によく使う式なので,確実に覚えておきましょう!
ちなみにこの式,重要なのにも関わらず,名前がありません。
頻繁に使う式に名前がないのは不便なので,このサイトでは今後この式を「波の基本式」と呼ぶことにします!
今回のまとめノート
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。
次回予告
次回は波をグラフで表すことについて考えてみましょう!