熱の分野も残すところあとわずかですが,最後は気体の状態変化についてお届け!
状態変化というと普通は気体・液体・固体間の変化を思い浮かべると思いますが,ここでいう気体の状態変化とは気体の圧力や体積,温度を変化させることを指します。
圧力・体積・温度の3つは状態方程式によってお互い関係し合っているので,普通はどれか1つを変化させると残りの2つも変化します。
しかし,3ついっぺんに変化すると調べるのが大変なので,3つのうち1つを変化しないようにして変化させるのが一般的です。
例えば体積を変化しないようにした場合,気体はどのように振る舞うでしょう?
体積が一定 = 気体のする仕事はゼロ
気体が入っている容器の容量が変化しない状態で行われる状態変化を,定積変化(等積変化)といいます。
それだけだと,「体積が変化しないから何なの?」となってしまうので,もうちょっと踏み込んで考えてみましょう。
状態方程式やボイル・シャルルの法則も悪くありませんが,気体の状態変化は基本的に熱力学第1法則を使って調べます。
つまり,第1法則に登場するQ, ⊿U,Wの3つに焦点を当てて考えていくことになるのですが……
もう熱分野も終盤なので,この時点でピンときてほしい!
Q, ⊿U,Wのうち,気体の体積と密接に関係しているのはW(気体がする仕事)ですよね!!
定積変化 → あー,体積が変わらないんだふーん
ではなく,
定積変化 → 体積が一定 → 気体は仕事をしない → W=0だ!!
と連想してください!
言葉を文字どおりに受け取らず,ちゃんと物理的な意味に結び付けることが大事です。
定積変化と熱力学第1法則
定積変化 → W=0ということがわかったので,これを熱力学第1法則に当てはめてみると…
Q = ⊿U + 0
が得られます!
定積変化では気体に出入りする熱量の分だけ内部エネルギーが増減する,ということをこの式は表しています。
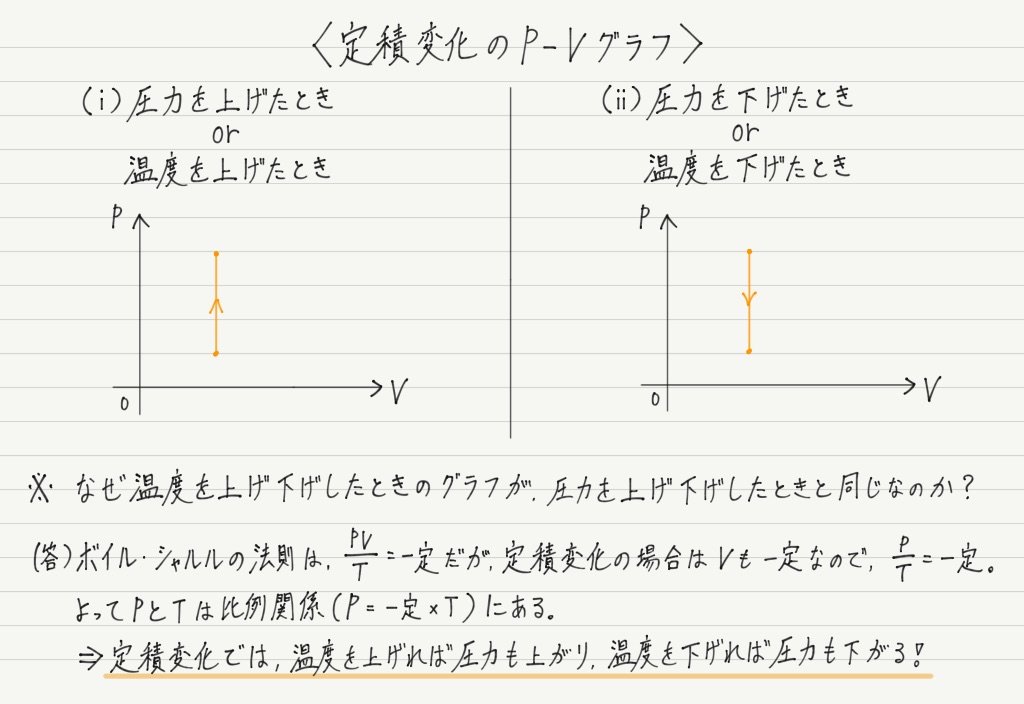
定積変化のP-Vグラフ
気体の状態変化ではP-Vグラフが頻出なので,定積変化の様子をP-Vグラフで表してみましょう!
別に難しいことはありません。
“定積”変化なのでVの値が変化しない,すなわち縦軸に平行なグラフになるはずです。
圧力変化だけでなく,温度変化もグラフから読み取れるようにしておくこと!
短いですが今回はここまで。
この調子で状態変化をひとつずつ見ていったあと,最後にそれらをまとめる予定なので今回はまとめノートはありません。
演習問題は用意してあるので,チャレンジしてみてください!
次回予告
圧力が一定の変化について調べていきましょう!