ここまで，気体のもつ性質について，圧力や体積，温度に注目してきましたが，気体とはそもそも多数の気体分子の運動によってできあがっているものです。
そこで今回は，気体の性質を分子の運動の観点から解き明かしてみたいと思います。
分子の「運動」ということで，力学の知識が必須になります。 特に，運動量の考え方について不慣れな方はまずそちらを復習してください。
力学はバッチリ！という方は，さっそく本編に突入しましょう！
計算をはじめるにあたって
計算の前に，問題をしっかりと設定しておきましょう。
これから考える気体は，
・理想気体である。
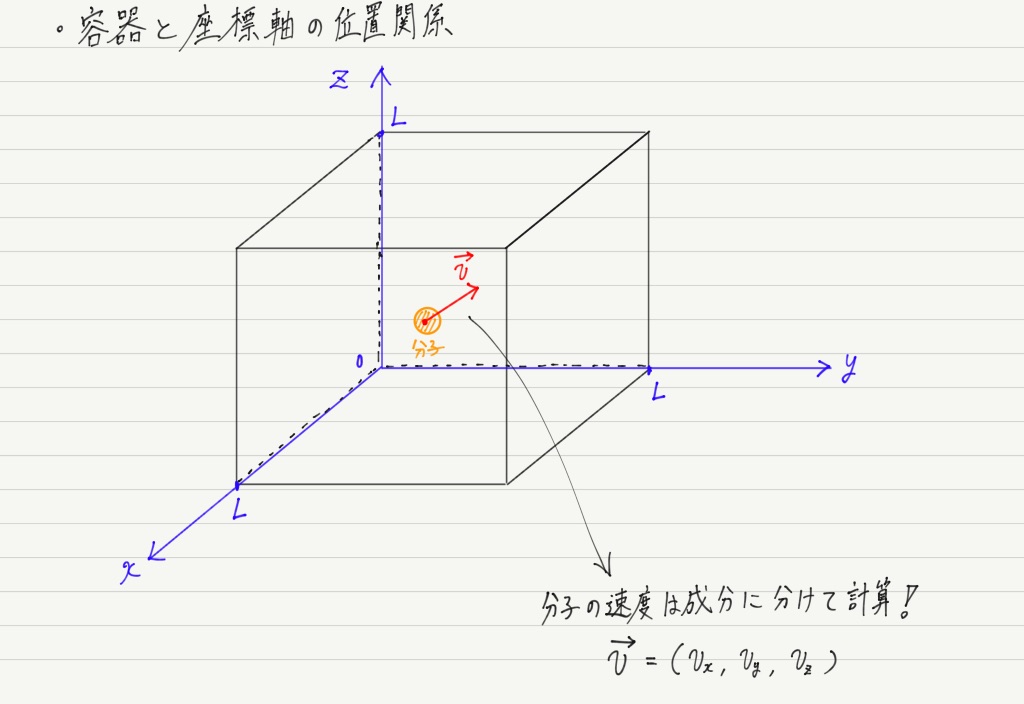
・気体は1辺の長さが Lの立方体容器に封入されている。
・容器内の気体分子の数をN個とする。
・気体分子1個の質量をmとする。
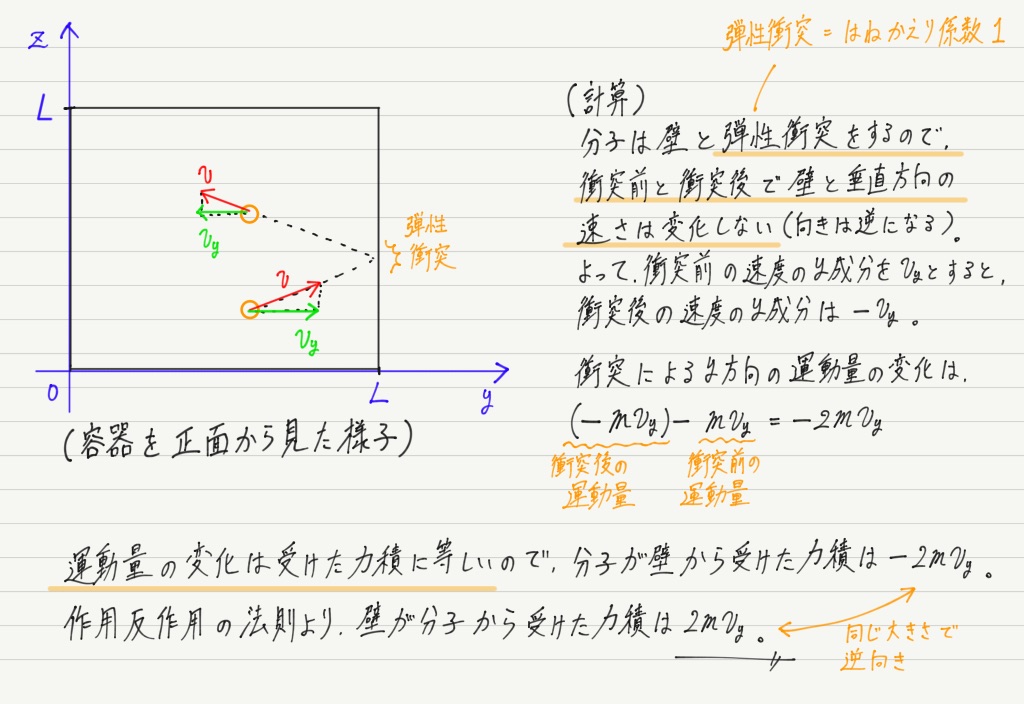
・気体分子と容器の壁は弾性衝突をする。
以上の条件を満たしているとします。
また，1つ目の「理想気体である」という条件からさらに，
・分子どうしは衝突しない。（理想気体では分子の大きさ無視するので，ぶつかることはない）
・分子は容器の壁にぶつかるまで等速直線運動をする。（理想気体では他の分子から力を受けないので，慣性の法則が成り立つ）
という条件も導かれます。 準備が整ったところで，さっそく計算をはじめていきますが，とりあえず気体の圧力を求めることを目標にしましょう。
なぜなら，圧力は気体分子が容器の壁と衝突することで生じるので，計算しやすそうだからです（衝突といえば運動量が使える！）。
手順１：1個の気体分子が1回の衝突で壁に与える力積を求める
今回は立方体の中の気体分子の運動なので，x方向，y方向，z方向という3次元の運動を扱うことになります。
3次元と聞いてビビらないでください。 2次元のときと同様に，成分に分けてそれぞれ計算するだけです。
成分ごとに計算するのですが，容器は立方体だし，気体分子はランダムに動き回っているので，どの方向も条件は同じ。
つまり，どれか1つの方向について計算すれば，まったく同じことが残りの2方向についても成り立つことになります！ これは楽チン！
そこで今回は，y方向に限定して計算してくことにしましょう。
まず，たくさんある分子の中の1つに注目します。 その分子のy方向の運動を考えると…
分子の運動量の変化から，壁が1回の衝突で受ける力積が求められました！
力に関係する情報は大きな収穫です！
手順２：気体分子が再び同じ壁に衝突するまでの時間を求める
気体分子は壁に衝突したあとも運動を続けるので，もうちょっと様子をみてみましょう。
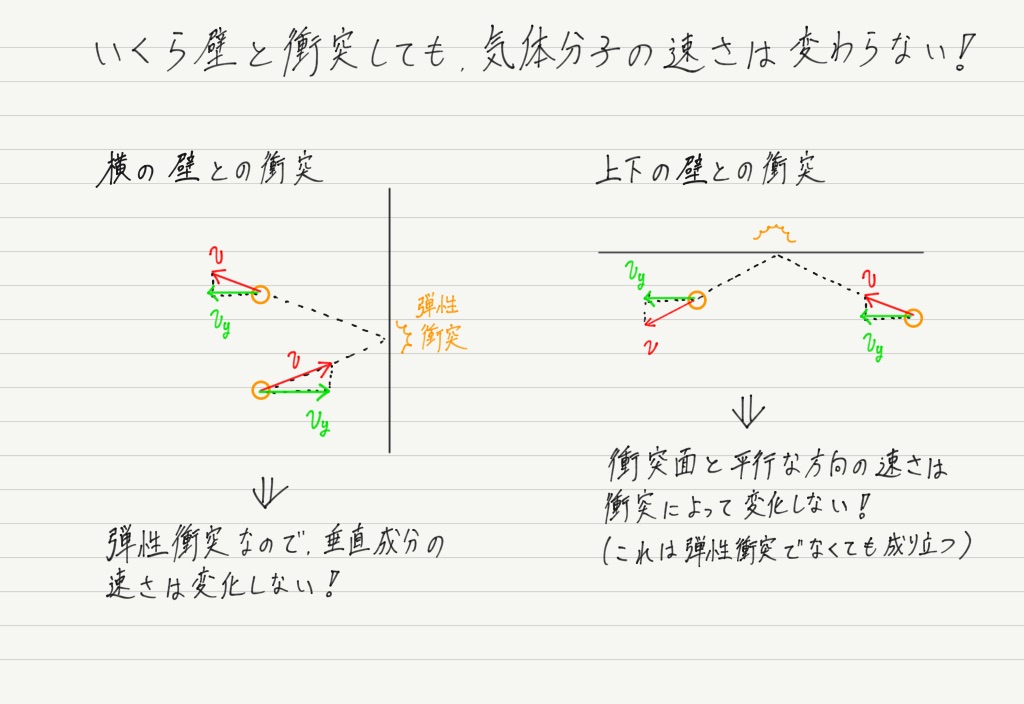
分子は容器の壁と衝突を繰り返すうち，さっき衝突した壁に再び衝突することになります。 このとき，どこの壁と何回ぶつかってもy成分の速さは変化しないことに注意してください（分子どうしは衝突しないという条件なので，壁の影響だけを考えればよい）。
つまり，いくら衝突してもy方向の運動は等速運動！
速さが一定ということは，再び同じ壁に衝突するまでの時間を計算することができそうです！
うーん，簡単！
手順３：気体分子が同じ壁に衝突する回数を求める
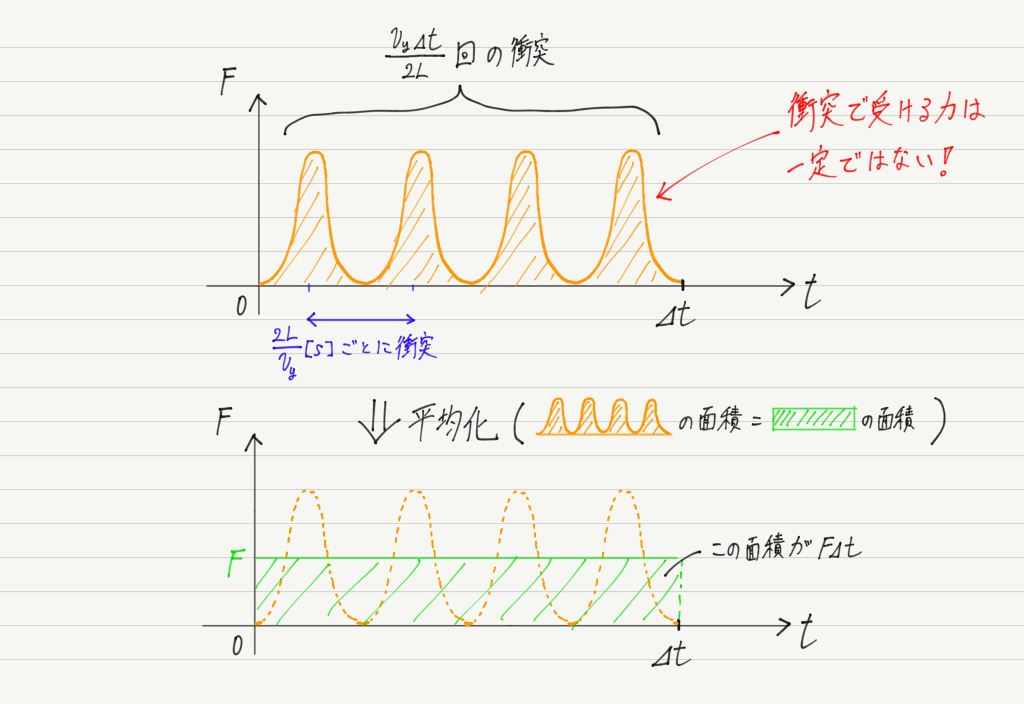
時間⊿ t［s］の間に，さっきの分子が何回同じ壁に衝突するかを，手順2の結果を使って計算しましょう。
ここでつまずく人が多いのですが，比を使って計算すれば簡単です。
さぁ，どんどんいきましょう！
手順４：1個の気体分子が壁に与える力を求める
とりあえず今回のクライマックスはここ。
手順1と手順3の結果を元に，壁が分子から受ける力を求めます。
式を見ると，Fは一定値のように見えますが，実際は衝突の度に瞬間的な力を受けるので，Fは一定ではありません。
いま求めたFは，壁が受ける力の平均であることに注意してください。
ともあれ，これで力を求めることができました。
計算はまだまだ続きますが，今回はここまで！
あ，今回はまとめノートはありません（手順1〜4を書き直しただけのまとめノートになってしまうので）。
分子運動論は，結果そのものよりも，結果に至るまでの計算過程が大事なので，ぜひ演習問題を自分の手を動かして解いてみてください。
次回予告
今回の計算の続きをしていきます。 壁が受ける力が求められたということは，気体の圧力について何か分かりそうな予感？？
