前回学習したボイル・シャルルの法則はわかりやすいし便利なのですが，気体の出入りがあると使えなくなってしまいます。 今回はボイル・シャルルの法則が使えない状況でも役に立つ，より一般的な法則を紹介したいと思います！
（今回以降，化学で学習する物質量［mol］の概念が登場します。分かっている前提で話を進めますので，未習の方は自力でなんとかしてください笑）
標準状態の気体とボイル・シャルルの法則
気体の分野では「標準状態の気体」というのがよく登場します。
標準状態とは，0℃，1気圧の状態のことを指します。 これはすぐ言えるようにしておきましょう。
では，標準状態の気体にボイル・シャルルの法則を適用してみましょう。 気体の物質量は n［mol］とします。 すると…
今回のタイトルにもなっている「理想気体の状態方程式」が得られました！
計算に現れた R＝8.31 J/(mol・K)を「気体定数」と呼びます。
ボイル・シャルルの法則は気体の種類によらず成り立つし，1molの気体の体積も気体の種類に関係なく22.4Lなので，上で行った計算は酸素でも窒素でもヘリウムでも，空気のような混合気体でも，どんな気体でも成り立ちます！
状態方程式は万能！！
ボイル・シャルルの法則再考
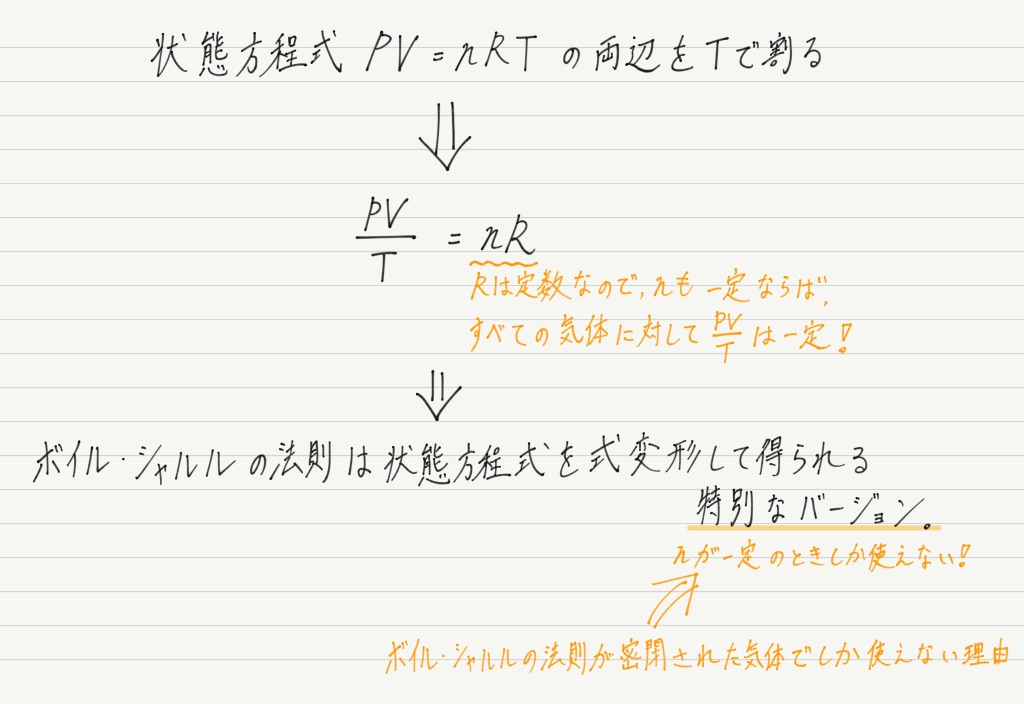
上ではボイル・シャルルの法則から状態方程式を導きました。 歴史的に見ても，ボイルの法則→シャルルの法則→状態方程式ですが，すべてが明らかになってみると，もっとも広い適用範囲をもつのは状態方程式です。
なので，歴史的には「ボイル・シャルルの法則から状態方程式が導かれた」が正しくても，物理的には「状態方程式を式変形したものがボイル・シャルルの法則」と見るのが正しいでしょう。 そのように考えれば，冒頭で述べたボイル・シャルルの法則の欠点も理解できます。
状態方程式 個数ver.
気体は膨大な数の分子からできているので，気体の量を物質量n［mol］で表すことが（特に化学では）多いですが，物理では分子の量を1個，2個，…というように，直接個数を数えることもあります。
そこで，物質量を用いた状態方程式PV＝nRTの他に，個数を用いるバージョンの状態方程式も紹介しておきます！
やることはPV＝nRTをちょっと式変形するだけ！
これで，個数バージョンの状態方程式PV＝NkTが得られました！
気体定数に代わってボルツマン定数という新しい定数が登場しましたが，方程式そのものよりも，このボルツマン定数の方が大事（ボルツマン定数の定義を覚えて，状態方程式の方は自分で導けるように！）。
高校の物理までは気体定数が幅を利かせてるけど，大学物理に進むと一転してボルツマン定数ばかり出てくるんだなぁ，これが（笑）
あくまで “理想気体の” 状態方程式！
最後に。
さきほど「状態方程式は万能！！」と書きましたが，半分ホントで，半分ウソです笑
半分ウソ，というのは，この式は理想気体の場合にしか使えないからです。 実在気体の場合には式の形がまた違ってきます。
半分ホント，というのは，高校物理の問題では理想気体として振る舞う気体しか扱わないからです。 どんな法則であれ，常に適用範囲を意識しておくことが大事です。
今回のまとめノート
時間に余裕がある人は，ぜひ問題演習にもチャレンジしてみてください！ より一層理解が深まります。
次回予告
気体は分子からできているので，分子の運動を計算すれば気体の性質がわかるのでは…？
ということで，次回から数回に渡って気体の分子運動を調べていきます！ 力学の知識をフル活用するので，心してかかってください。
