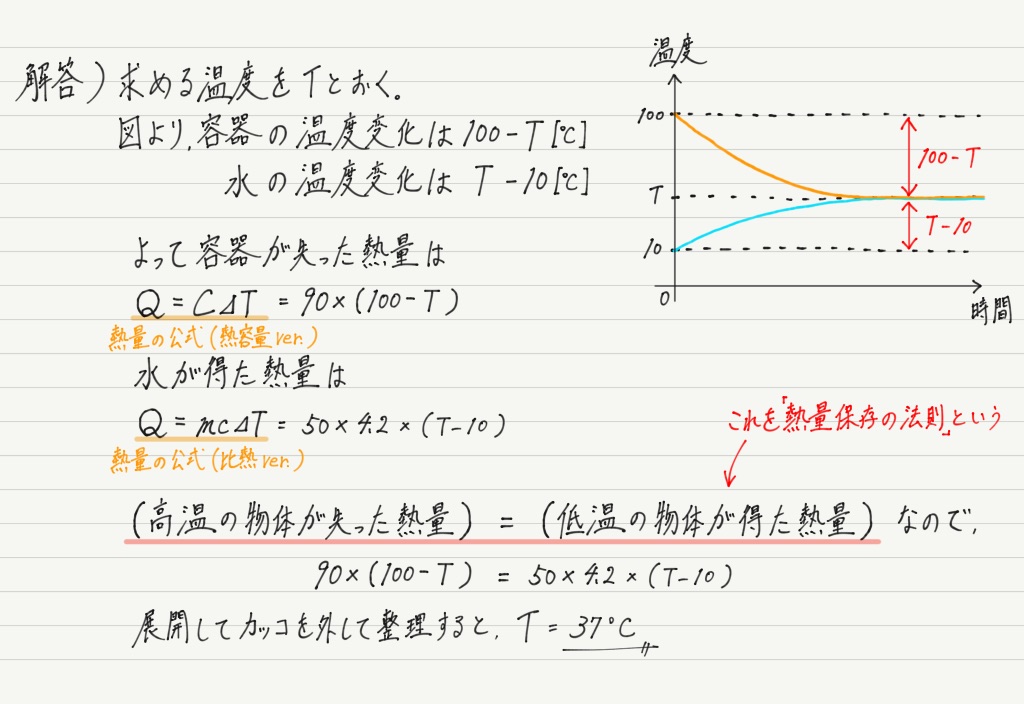
【問】100℃に熱した容器(熱容量90J/K)に10℃の水を50g入れた。 時間が経つと,容器と水は同じ温度になった。それは何℃か。 ただし,熱のやりとりは容器と水の間だけで起こるものとし,水の比熱を4.2J/(g・K)とする。
いきなり問題でびっくりしましたと思いますが,今回もはりきって勉強していきましょう!!
まずは上の問題。 教科書によくある典型問題ですが,苦手とする人が非常に多いです。 この手の問題にどうやってアプローチすればいいのか順を追って見ていきましょう。
よくある間違い
数字がいっぱい出てきて混乱しそうですが,計算を始める前にまずは何が起こっているか確認しましょう。
「熱い容器に冷たい水を入れたら,ある温度に落ち着いた」
起こっていることはこれだけです。
温度差がある物質を一緒に置いておくと,それらはやがて同じ温度になり,その後温度は変化しなくなります(熱平衡という)。
つまりこの問題は「容器と水が熱平衡になったときの温度を求めよ」という,ただそれだけの問題です。
さて,この問題で初学者がよくやってしまうミスがあります。
(よくある間違い)
100℃と10℃の中間だから,(100+10)÷2=55℃ 答え:55℃
確かに,熱平衡の温度は高い温度と低い温度の間の温度になります。
しかし,ちょうど真ん中になるとは限りません。 正しい解答を見てみましょう。
解答・解説
この問題を解くポイントは熱のやり取りです。 熱平衡は,高温の物体から低温の物体へ熱を受け渡すことで起こります。
熱はエネルギーのひとつですが,エネルギーは勝手に生まれたり消えたりしません。
つまり,高温の物体が出した熱量は,すべて低温の物体が受け取ることになります。
先ほどの「よくある間違い」はどこが間違いだったのかというと,物体ごとの温まりやすさのちがいを考慮していなかった点です。 同じ熱量を受け渡ししても,温度の増減は同じではないので,真ん中の温度にはならないのです。
おまけ
せっかくなので最後にもう1問。 今度は物体が3つのパターン。
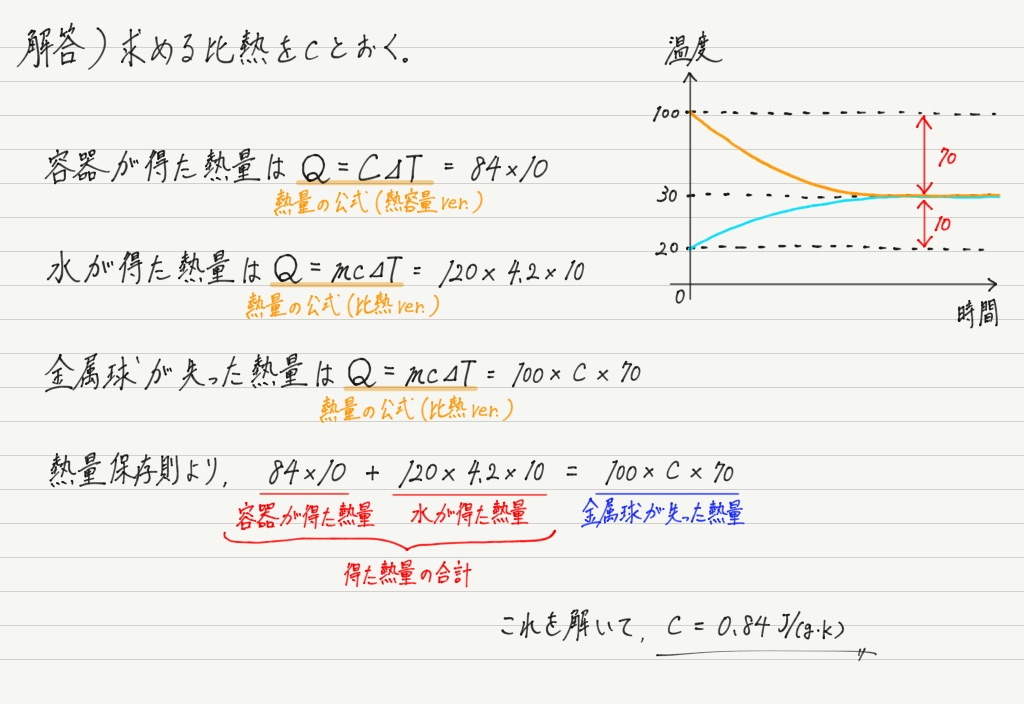
【問】熱容量が84J/Kの容器に120gの水が入っていて,温度は20℃で一定であった。 この中に100℃に熱した100gの金属球を入れたところ,全体の温度が30℃になった。この金属球の比熱を求めよ。 ただし,熱のやりとりは容器と水と金属球の間だけで起こるものとし,水の比熱を4.2J/(g・K)とする。
物体の数が増えても「熱量を失うのはどの物体か,得るのはどの物体か」に注目すれば同じように解くことができます。
ちなみにこの問題は金属球の比熱を求めるわけですが,比熱は金属の種類ごとに異なるので,この計算をすることで球が何の金属でできているのかおおよそ分かります。
では解答です!
温度 “変化” へ代入するときは℃のままでOK
ところで,最初の問題といまの問題の解答を見て,あれっ?と思うところはありませんでしたか? 熱量の公式の⊿Tに代入する温度変化のところです。
前回,前々回の記事を見返してもらえると,⊿Tの単位はK(ケルビン)になっているのに,今回の解答では℃のまま計算しています。
これは,⊿Tが温度 “変化” なので,℃で計算してもKで計算しても結局同じ値になるということを利用しているのですが,まぁ,実際にやってみましょう。
「20℃の物体を熱して70℃にした。温度変化は何℃か。また何Kか。」
まずは℃でそのまま計算してみます。 20℃→70℃なので温度変化は当然+50です。
次はKに直してから計算してみます。 20℃は293K,70℃は343Kです。
293Kと343Kの差を求めるとやはり+50になります。
セルシウス温度と熱力学温度は,基準はちがうけど目盛り幅は同じなので,「1℃上がる」ことと「1K上がる」ことは同じ意味です!
今回の問題の解答で,Kではなく℃のまま計算していた理由はここにあります。
今回のまとめノート
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。
次回予告
計算おつかれさまでした! 次回は物質の状態変化をやります。