「物理は計算が難しい…」という声をよく耳にしますが，高校物理で必要となる数学の知識はほとんど中学数学です。
高校で習う数学が必要となる場面はほぼない…と言いたいところですが，三角比（三角関数）だけは例外で，物理にかなりの頻度で登場します。
そこで今回は，
「数学で習ったときもわからなかったのに，物理で使うなんて無理…」
「数学で習う前に物理で出てきちゃって何がなんだかわからん…」
という人に向けて，簡単に三角比・三角関数について解説したいと思います！
三角比の意味
突然ですが，三角比という名前の由来を考えましょう。
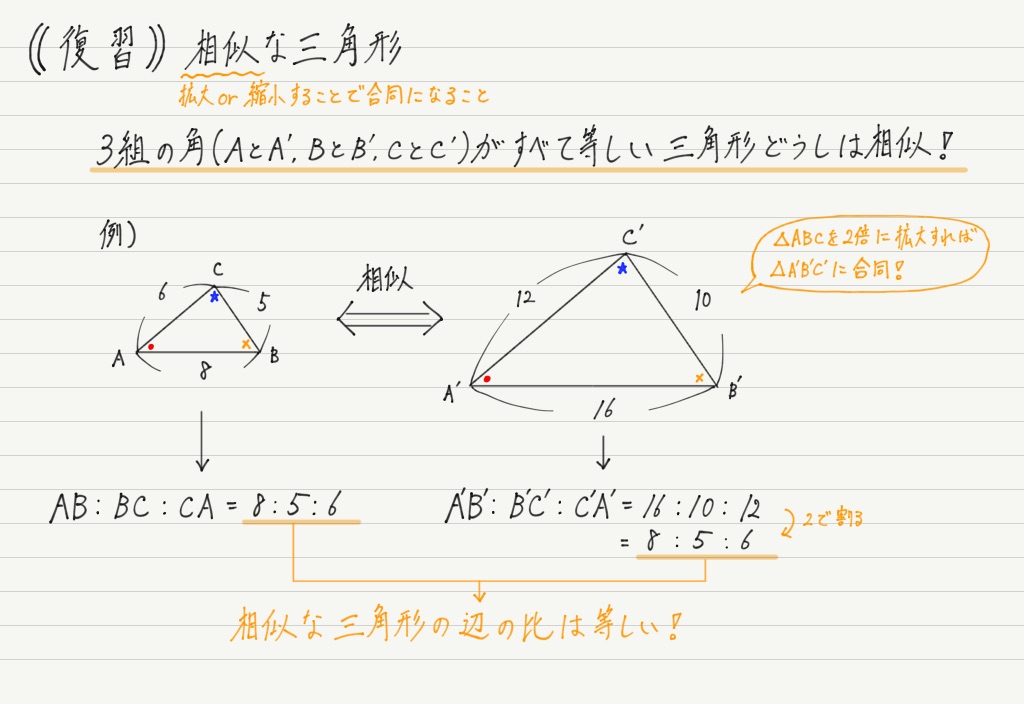
“三角” の “比” 。 三角で比といえば相似が思い浮かびます。 ここで軽く復習タイム！
ひとつ補足しておくと，三角形が相似になる条件は「3組の角が等しい」ではなく「2組の角が等しい」です。
なぜかと言うと，三角形の内角の和は180°と決まっているから。
例えば∠A＝∠A’＝40°，∠B＝∠B’＝60°ならば，あとは自動的に∠C＝∠C’＝80°と決まります。 よって角度は2組だけ同じであれば十分なのです。
わかったことをまとめると，「2組の角が同じならば相似であり，相似ならば辺の比は等しい。 」
これは言い換えれば，「2つの角が決まれば辺の比も決まる」ということ。
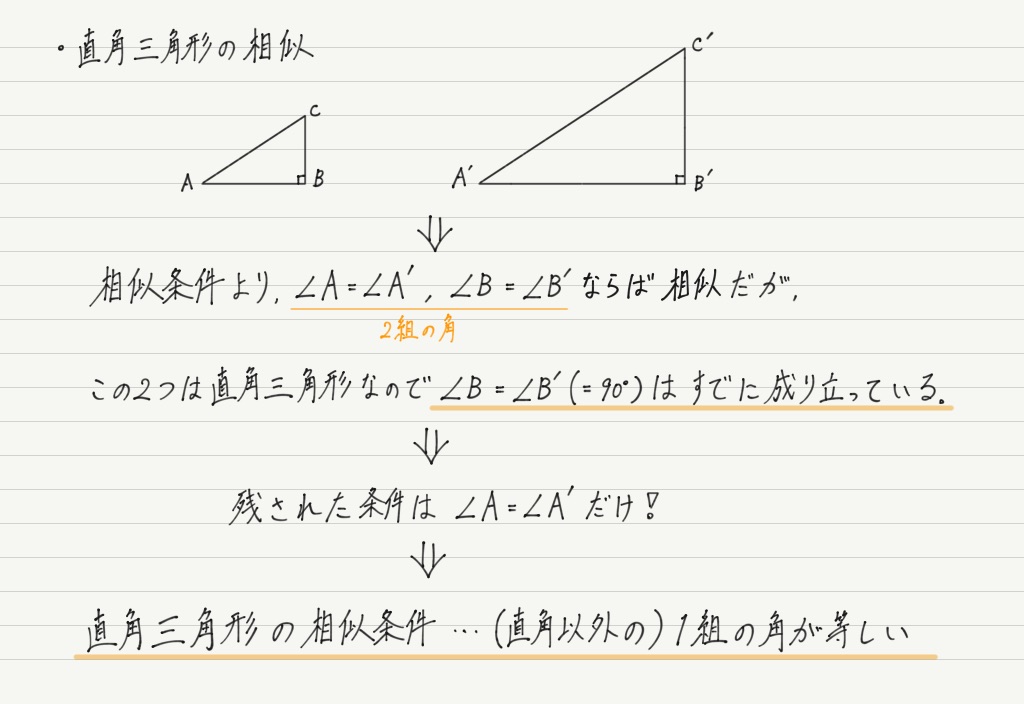
ところで三角比の “三角” は，実は直角三角形のことを指しています。
いまの相似の話を直角三角形に当てはめてみましょう。
つまり直角三角形の場合，相似かどうかは1つの角度だけで決まってしまう。
辺の比の話と合わせて考えると，「直角以外の1つの角が決まれば辺の比も決まる」
ことになります。
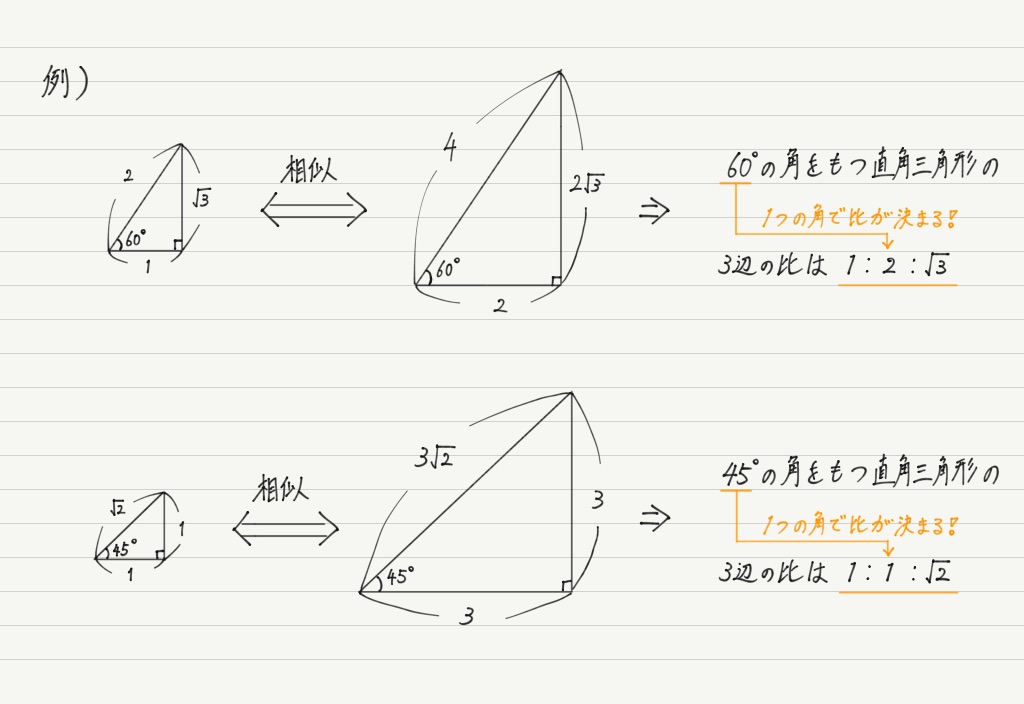
たった1つの角度だけで3辺の比がわかってしまうというのはすごくないですか！！
こんな強力な性質，使わなきゃもったいないでしょ！
…ってことで，直角三角形の “1つの角度” と “辺の比” を結びつけたものが三角比の正体です。
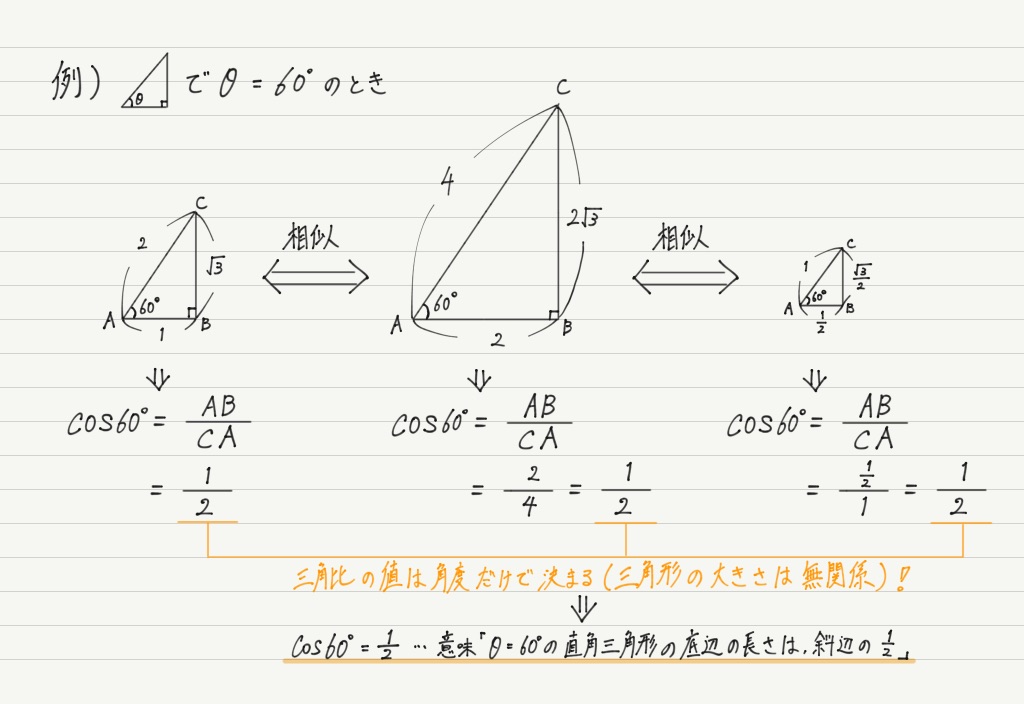
この図の一番右の三角形に注目すると，「cosθは斜辺の長さが1の直角三角形の底辺の長さを表している」とも解釈できます。 この見方は三角比から三角関数の学習にステップアップする上で非常に重要。
（同様に，「sinθは斜辺の長さが1の直角三角形の高さを表している」と解釈できる。）
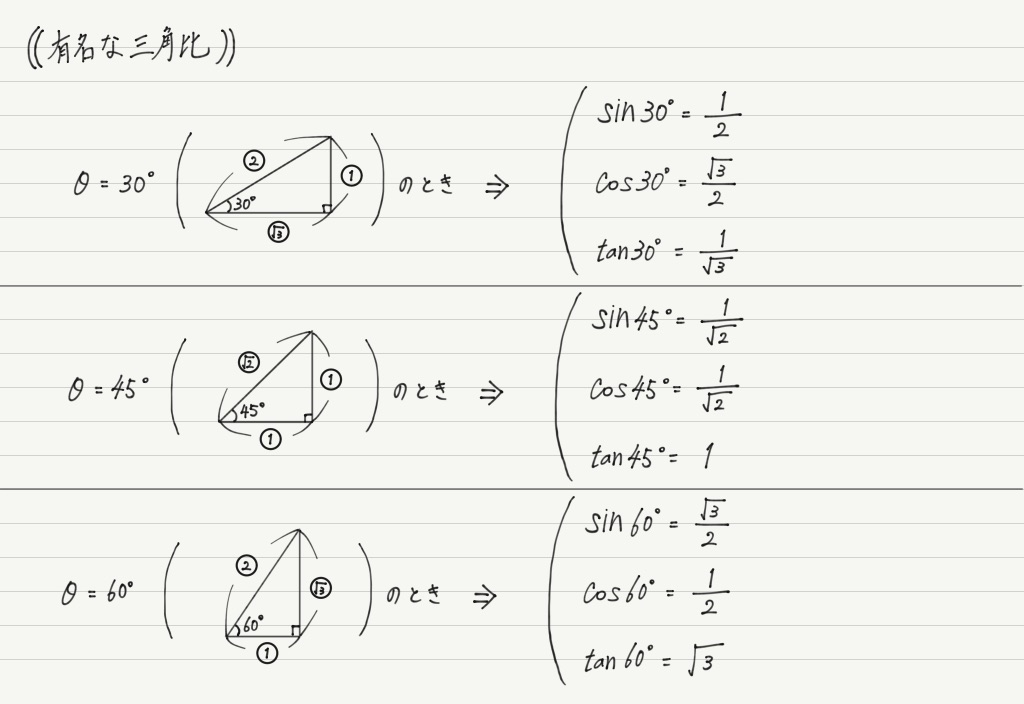
あ，そうそう，例に挙げたθ＝60°の直角三角形のように，角度と辺の比がわかっているものについてはsin,cos,tanの値をちゃんと言えるようにしておくのが大人のマナーですよ（？）
それから，sin,cos,tanについて次のような関係式が成り立つこともわかります。
式だけじゃなく導出の仕方も頭に入れておくことをオススメします。
自分は物理基礎までしかやらないよ，っていう人はここまでの内容を理解していればとりあえずOK。
物理基礎で三角比を使う場面はほぼ力の分解に限られるので，あとは問題演習を積んで使いこなせるようにすること。 使ううちに「三角比って便利だなぁ」と実感することでしょう！
三角比を用いた力の分解の具体的なやり方はこちらの記事をご覧ください。
さぁ，物理基礎以上の物理をやる人はこの先が本番！
弧度法
三角関数の話に入る前にちょっと一息。
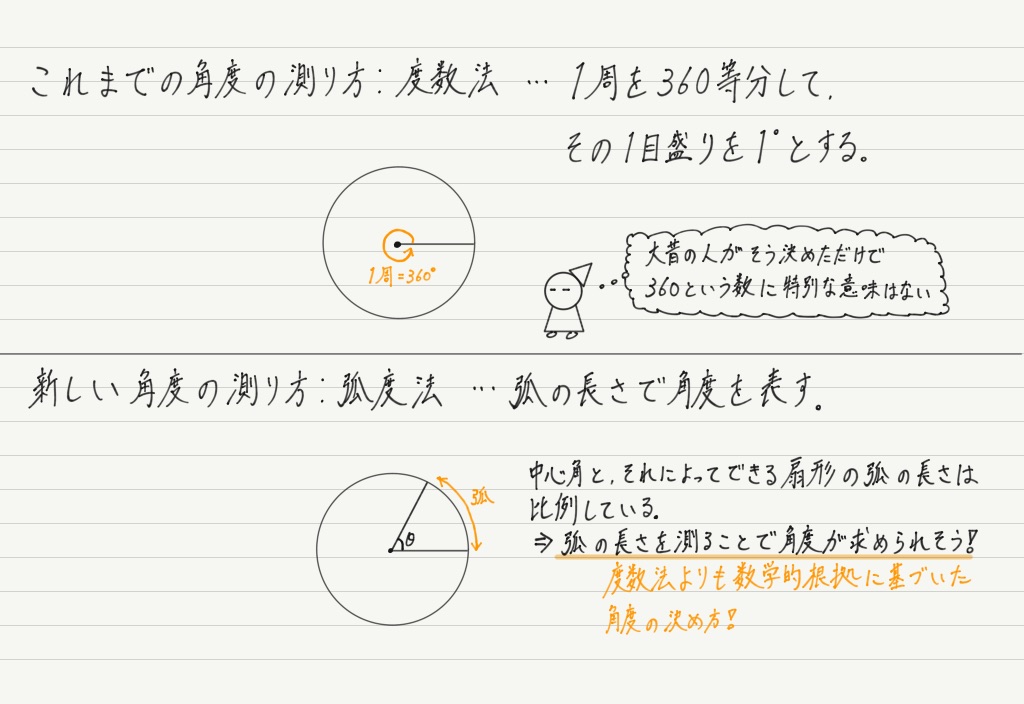
これまで角度は「度数法（直角は90°，360°で1周）」を用いていましたが，実はコレ，数学や物理をやる上ではあまり好ましくありません。
そこで，みなさんには「弧度法」という新たな角度の測り方を伝授したいと思います！
弧度法の基本的なアイデアは以下の通り。
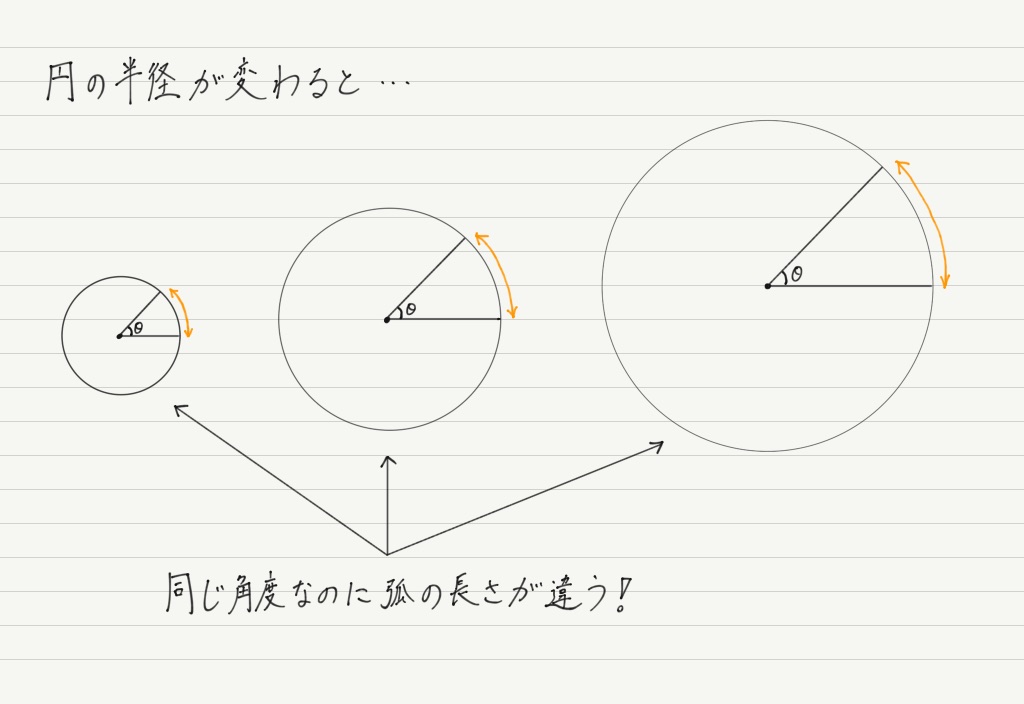
すごくいいアイデアに見えますが，ひとつ問題があります。
このように，使う円によって弧の長さがまちまちです。。。
これでは角度と弧の長さが結びつきません。
…しかしあきらめるのはまだ早い！
この不具合は円の大きさ（半径）が原因。 そこで，弧度法で角度を測るときは「半径1の円を用いる」とあらかじめ決めてしまいましょう！
最初はどうしても使い慣れた度数法のほうがやりやすいと感じると思いますが，弧度法は物理でも多用するので，早めにマスターしておくこと！
直角三角形からの卒業
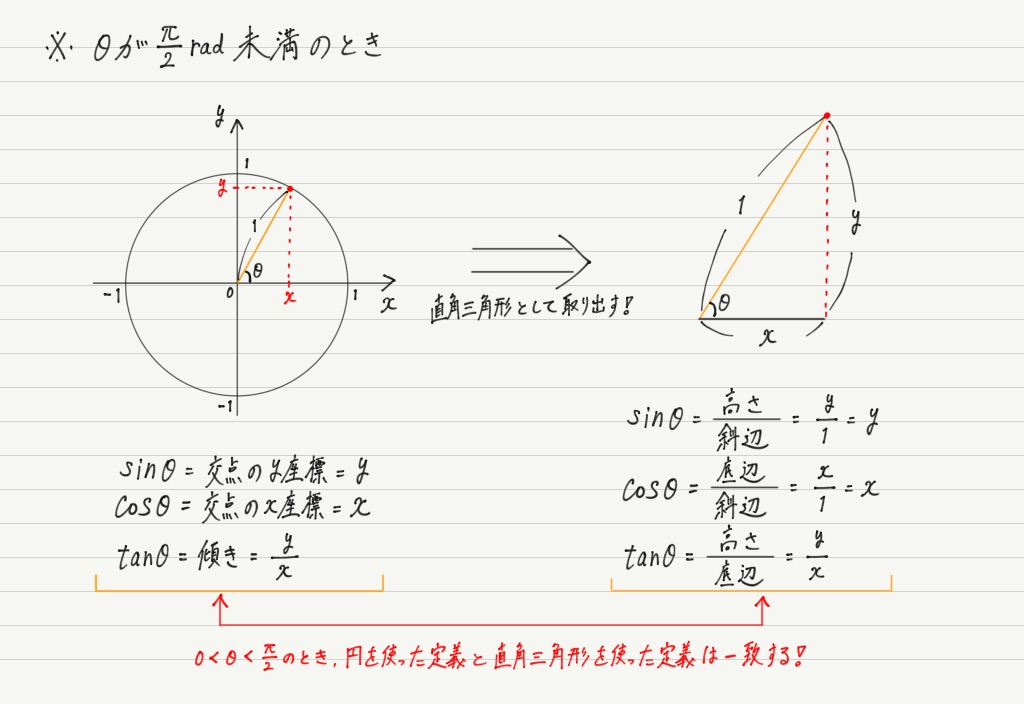
さて，角度と直角三角形の辺の比を結びつけるというのはとてもいいアイデアなのですが，ひとつ欠点があります。
このようにθが直角を超えると， 三角比の主役である直角三角形がつくれません。
せっかく便利な三角比なのにこれじゃもったいない！ すべての角度で三角比を考えたい！
ということで編み出されたのが，直角三角形を使わずにsin,cos,tanを決めてしまうやり方。
直角三角形とちがって，単位円と半直線との交点はθがどんな値であっても作図することができます！ これなら角度の制限ナシ！
θが直角未満のときは円を使って求めても，直角三角形を使って求めても，値は変わらないので安心してください。
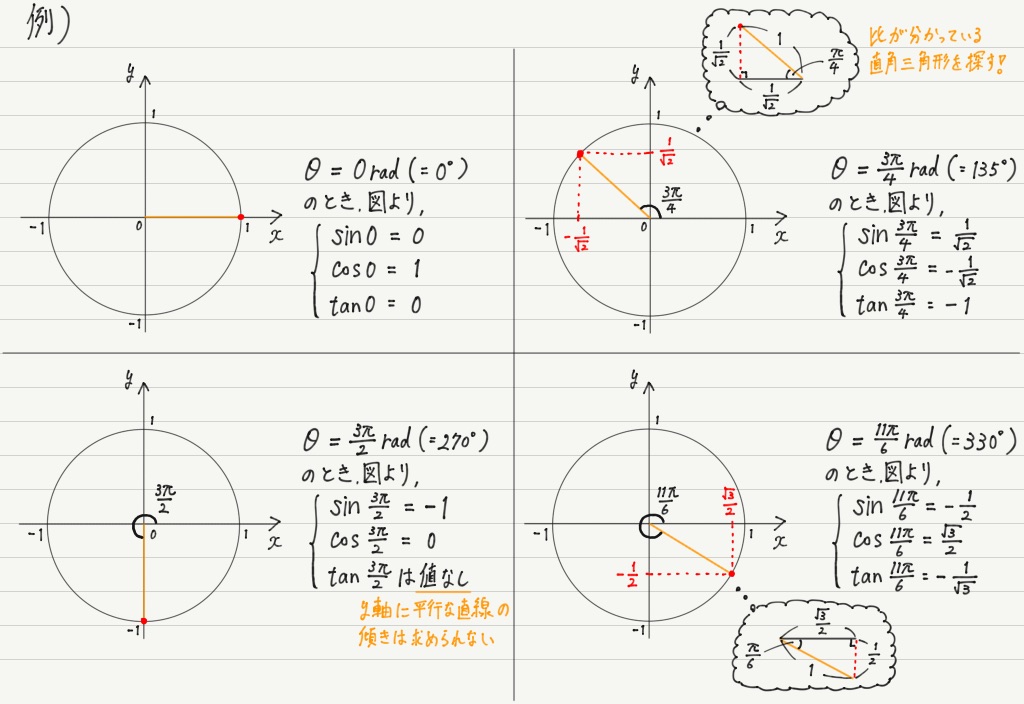
新しい定義によって，いろんな角度でsin,cos,tanの値が求められるようになったので，具体的にいくつか求めてみましょう。 その際，sin,cosは交点の“座標”なので，交点の場所によって符号が変わることに注意！
ところでこの円を使ったsin,cos,tanの定義，これはもはや “比” ではありません！(^_^;)
半直線の角度θと交点の座標を関連づけているので， “関数” と捉えるのが正しそう。 よって円を使って定義したsin,cos,tanのことを三角“比”ではなく，三角“関数”と呼ぶことにしたいと思います。
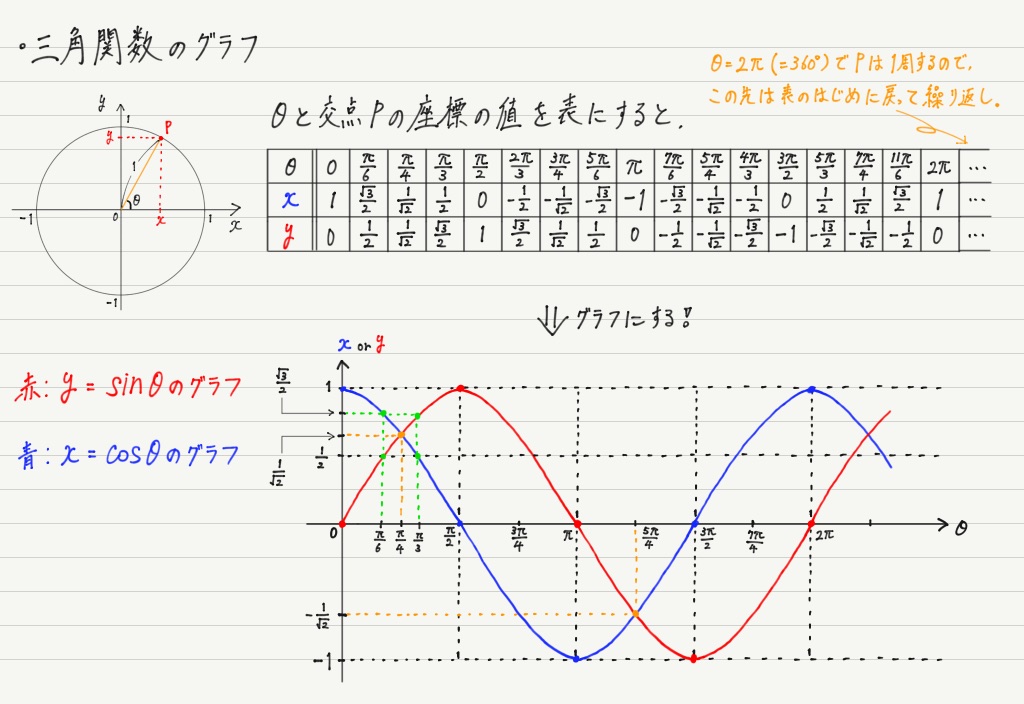
さて，関数と呼ぶことにしたからにはグラフを無視するわけにはいきません！ θの変化によって，sinθやcosθがどのように変化するのかをグラフで表してみましょう。
（※ tanθのグラフは物理ではほとんど使わないので割愛。）
交点Pは円周上をぐるぐるまわるだけなので，グラフにするとこのように延々と同じ形が続きます。 これこそが三角関数の特徴。
物理では延々と同じ運動を繰り返す現象がいくつもあります（単振動，波など）が，そういう現象を式で表現するときに三角関数は不可欠なのです。
今回の内容はこれでおしまい。 簡単な演習問題を用意したので，ぜひトライしましょう！
