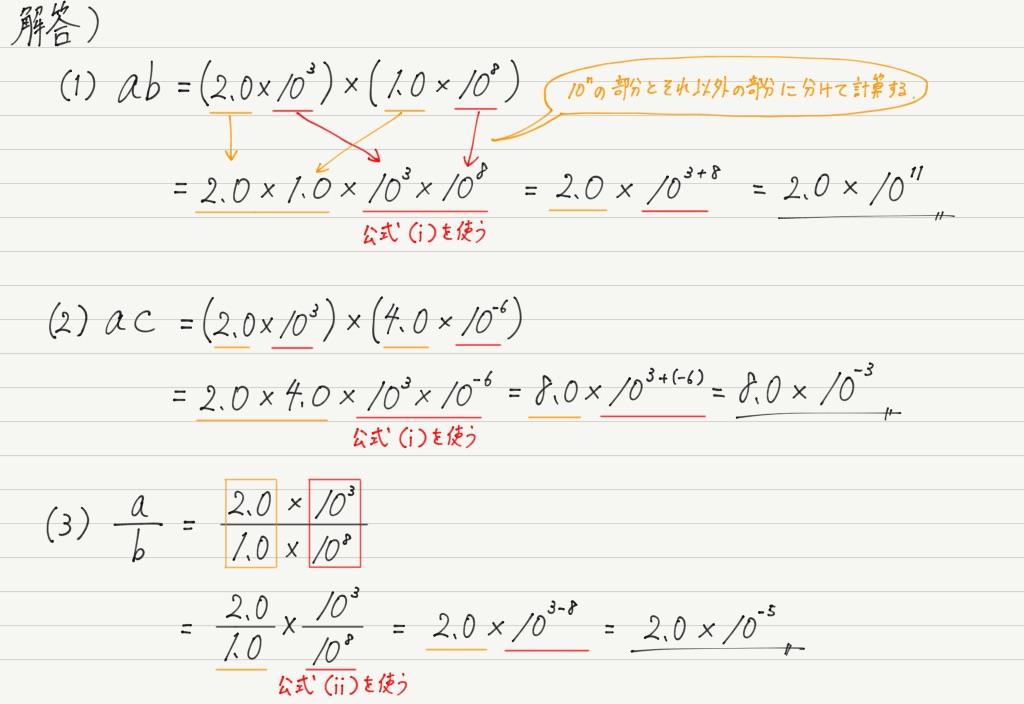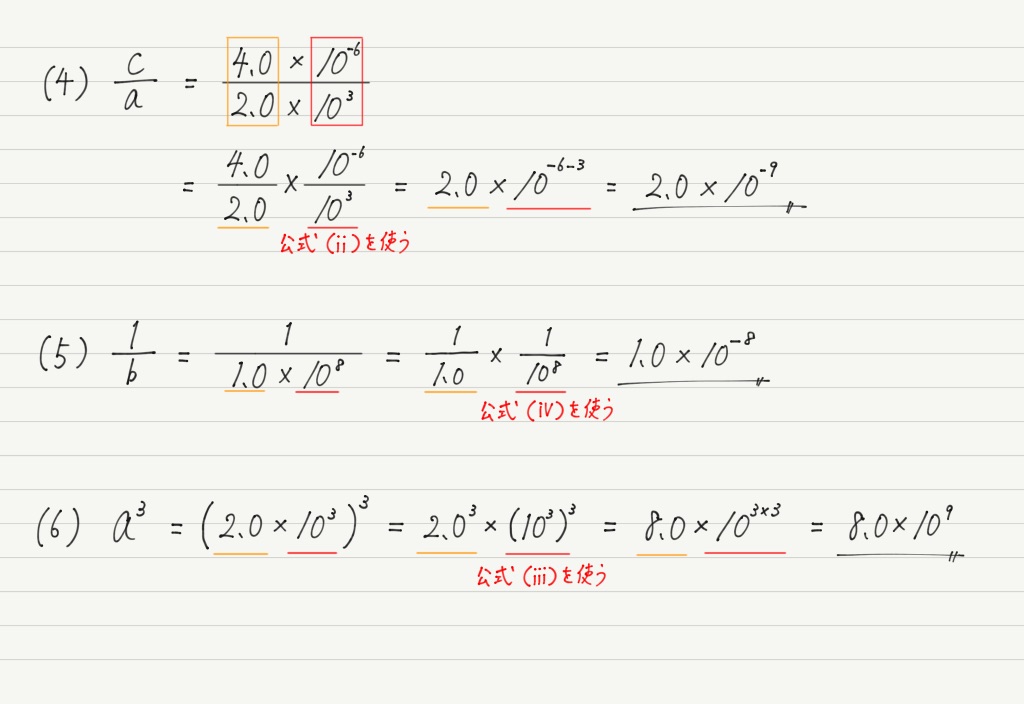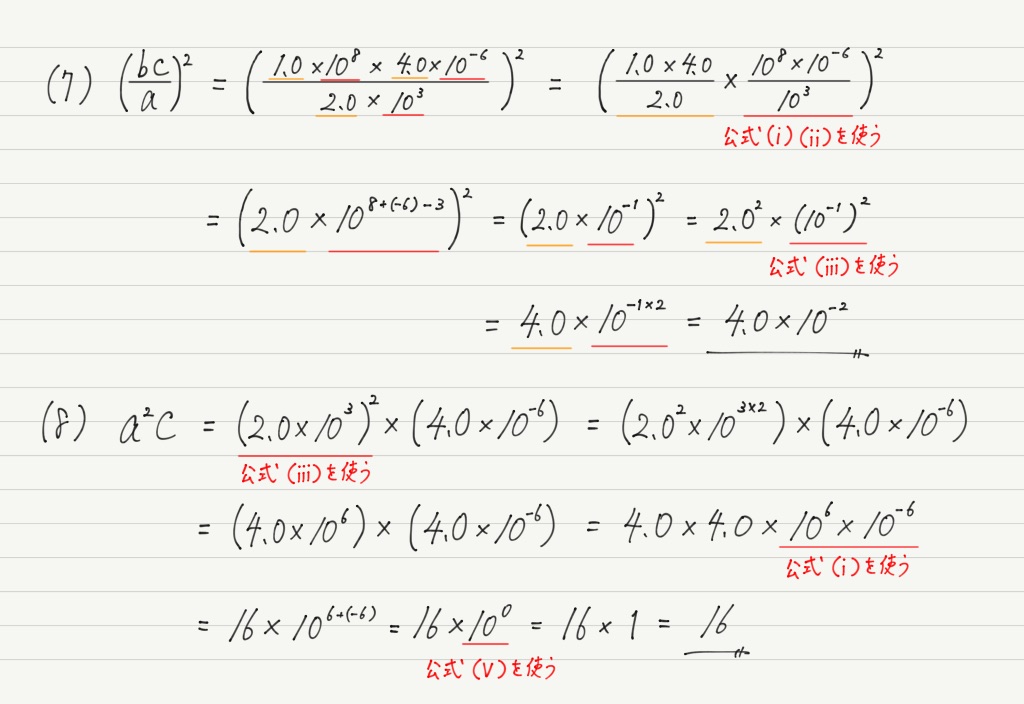物理では非常に大きい数や非常に小さい数が登場する場面が少なくありません。
例えば光の速さ 約300000000m/sだったり,
電気素量 約0.00000000000000000016Cだったり,…
こういった数はゼロが多すぎて読むのも大変だし,書くのも大変だし,ゼロの数を書きまちがえそうだし,計算しづらいし,とにかくデメリットだらけ。
今回はこのような大きすぎる or 小さすぎる数の表記について考えていきましょう。
大きい数の表し方
中学校で習いますが,同じ数を何回もかけたものを累乗といいます。
ここでは10の累乗を考えてみましょう。
このように10は1回かけるたびに位が1つずつ上がります。 これは使えそう!
…ってことで,大きい数は次のように表記することにしましょう。
この書き方なら横幅もとらないし,10の指数を見るだけで桁もわかるし,とても便利!
小さい数の表し方
大きい数が10の累乗を使ってうまいこと書けたので,小さい数も同じように書けたらいいのになーって思いますよね?
さて,10を何回もかけると位が上がりますが,逆に10で割りつづけると位がどんどん下がっていきます。
これを使えば小さい数もうまく表せそう!
そこで,次のような表記を採用します。
「マイナス◯乗」は初めて見ると面食らいますが,かけ算ではなく割り算を表しているということを頭に入れておけば大丈夫。
これを利用すると小さい数は次のように書けます。
大きい数も小さい数もこれひとつ。 10の累乗の万能さよ…
指数の計算
物理の教科書・問題集などを見てもらえばわかりますが,10の累乗はかなり頻繁に登場します。
必然的に10の累乗どうしの計算も多くなります。
これに対して初心者がやりがちなのが次の解答。
この解答は間違いではありません。
だけどせっかく10の累乗で表したのに,それをまた0の羅列に直したら結局0の数を数えるハメになってただの二度手間!!
ゼロの数え間違いによる計算ミスも多発します。
じゃあどうすればいいのかというと,指数に関する公式の活用です。
この公式でa=10とすると,さっきの問題は楽勝!
途中計算も丁寧に書いたのでちょっと長くなってしまいましたが,実際に計算するときはほとんど暗算でできちゃうので,さっきのダメな解答例に比べて圧倒的に速いです!
なによりこのやり方だと「0の数を数える」という行為をしなくて済むので計算ミスもグンと減ります。
いいことづくめなので,指数の公式は自然に使いこなせるようになるまで練習してください。
10の累乗の使いどころ
10の累乗のありがたみを知ってもらいたくて,冒頭ではすごく大きい数やすごく小さい数を例に出しましたが,実際はそこまで極端に大きかったり小さかったりしなくても10の累乗を使って表します。
今回の話はこれでおしまいですが,時間に余裕がある人はぜひ問題演習にもチャレンジしてみましょう!
より一層理解が深まります。
10の累乗を使った数値の表し方は有効数字とも関係してくるので,未読の方はそちらも一読してください!