せっかくRLC回路についての知識が増えてきたところなので,このまま終わるのはもったいない!
もう少しだけ考察を続けてみましょう。
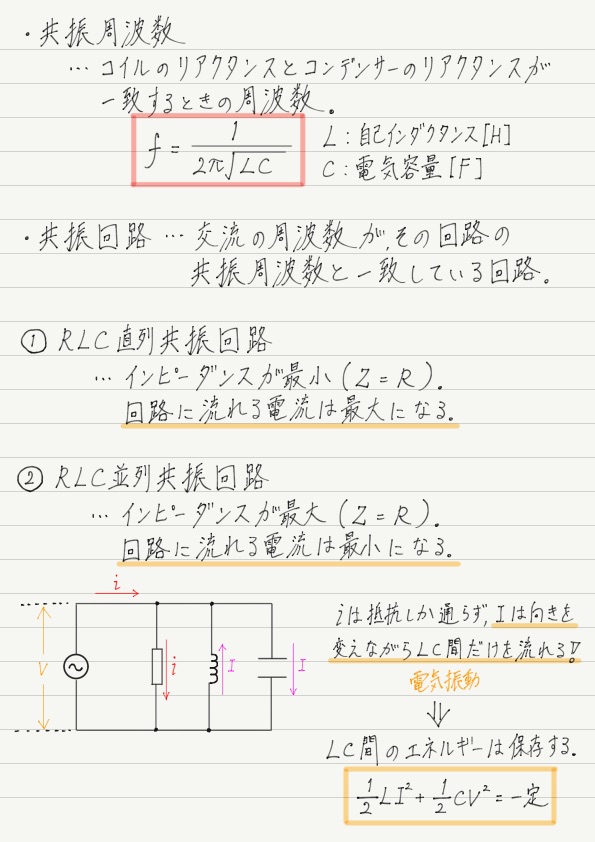
共振周波数
突然ですがリアクタンスの式を思い出してください。
コイルのリアクタンスは角周波数に比例するので,その効果は角周波数が大きい交流回路ほど顕著になります。
一方,コンデンサーのリアクタンスは角周波数に反比例するので,その効果は角周波数が小さい交流回路ほど顕著になります。
要するにコイルとコンデンサーが両方含まれている回路だと,角周波数が大きすぎても小さすぎても,どちらかのリアクタンスの効果が目立ってしまうということ。
…ん? てことは,大きすぎず小さすぎず,“ちょうどいい感じの角周波数” を選べば何か起こるのでは?
まずはその “ちょうどいい感じの角周波数” を求めてみましょう。
コイルとコンデンサー,2つのリアクタンスが同じ値になれば,どちらかが目立つということはなくなるので,
これが “ちょうどいい感じの角周波数” です!
計算はこれでいいのですが,角周波数ωではなく周波数 f で表すことのほうが多いようなので,もういっちょ式変形しておきます。
交流の周波数が,その回路の共振周波数にぴったり一致するとき,それを共振回路と呼びます。
共振回路ではいったい何が起こるのでしょうか?
直列共振
共振回路で何が起こるのかを理解するには,インピーダンスに注目するのが手っ取り早いです。
ちょっと脱線。
「共振」というワードは一度波の分野で学習していますが,覚えていますか?
元々の共振は,「特定の振動数(固有振動数)で揺らしたときに,物体が大きく振動する」という現象を指す用語でしたが,いまやっている直列共振は,「特定の周波数を与えると,大きな交流電流が流れる」とのことなので,ちょっと似ていますよね?
別の分野なのに同じ用語を流用しているのはこういう理由です。
話を戻しましょう。
直列共振の「特定の周波数で電流が最大になる」というのはとても面白い特性で,テレビやラジオの受信回路に利用されています。
受信したい周波数を共振周波数にもつ回路をあらかじめつくっておいて,目的の周波数では大きな電流を流し,それ以外の不要な周波数ではほとんど電流を流さないようにする,というわけ。
並列共振
並列の場合も同様にインピーダンスに着目しましょう。
並列も直列も共振時のインピーダンスはRで同じですが,直列のときは最小値だったのに対し,並列では最大値となります。
共振の条件は同じでも,直列と並列で振る舞いが真逆なので注意しましょう!
電気振動
この並列共振回路について,もうちょっと吟味してみましょう。
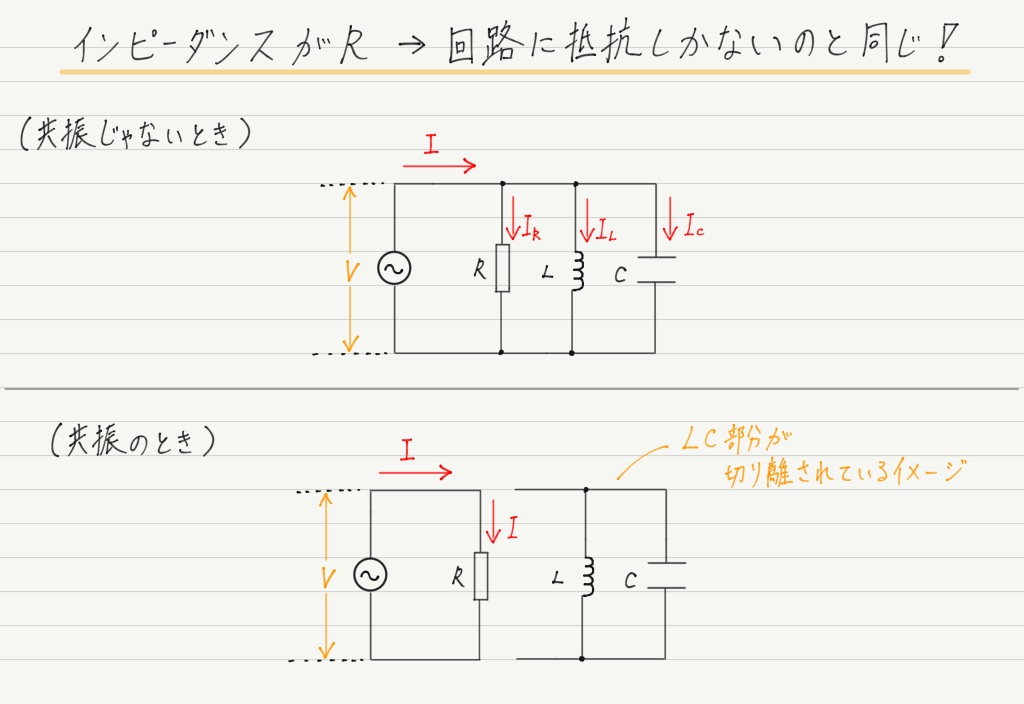
インピーダンスがRになるいう事実は,「LC並列部には電流が流れこまず,すべて抵抗側に流れこんでいる」と解釈していいでしょう。
では,コイルとコンデンサーにまったく電流が流れていないのかというと,それもハズレ。
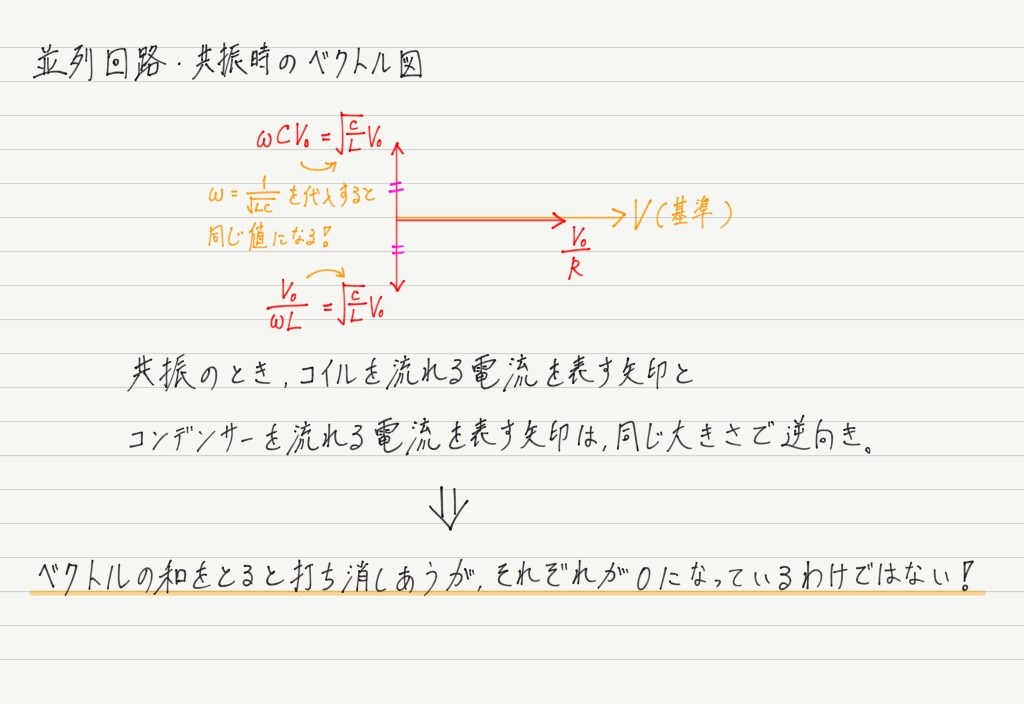
実はこのとき,「回路を流れる電流はLC並列部に流れこまないが,コイルとコンデンサーは互いに電流をやり取りしている」という状況になっています!
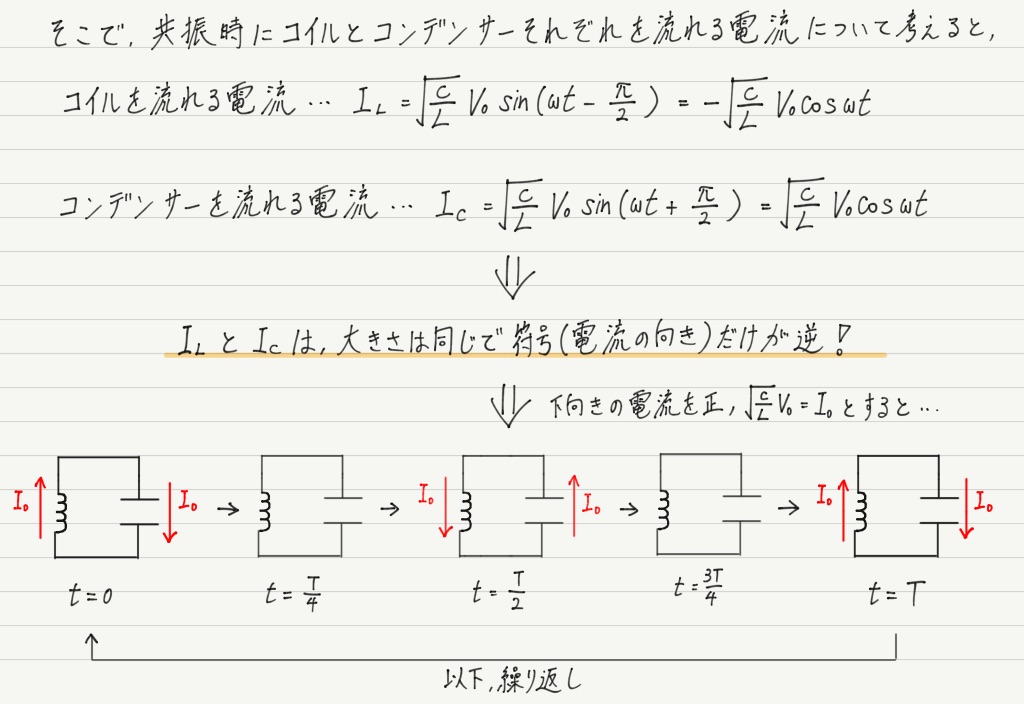
ちょっと計算してみれば,このことが理解できると思います。
このように,LC並列部に流れる電流のように周期的に電流の向きが変わる現象を電気振動といいます。
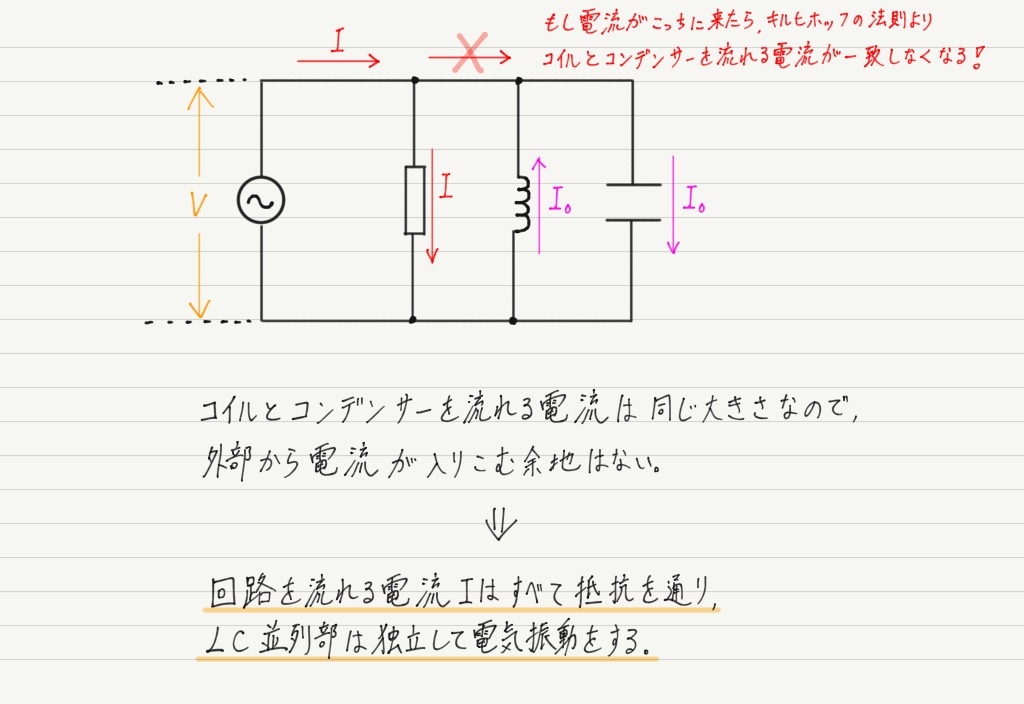
結局,RLC並列共振回路の全体像は,
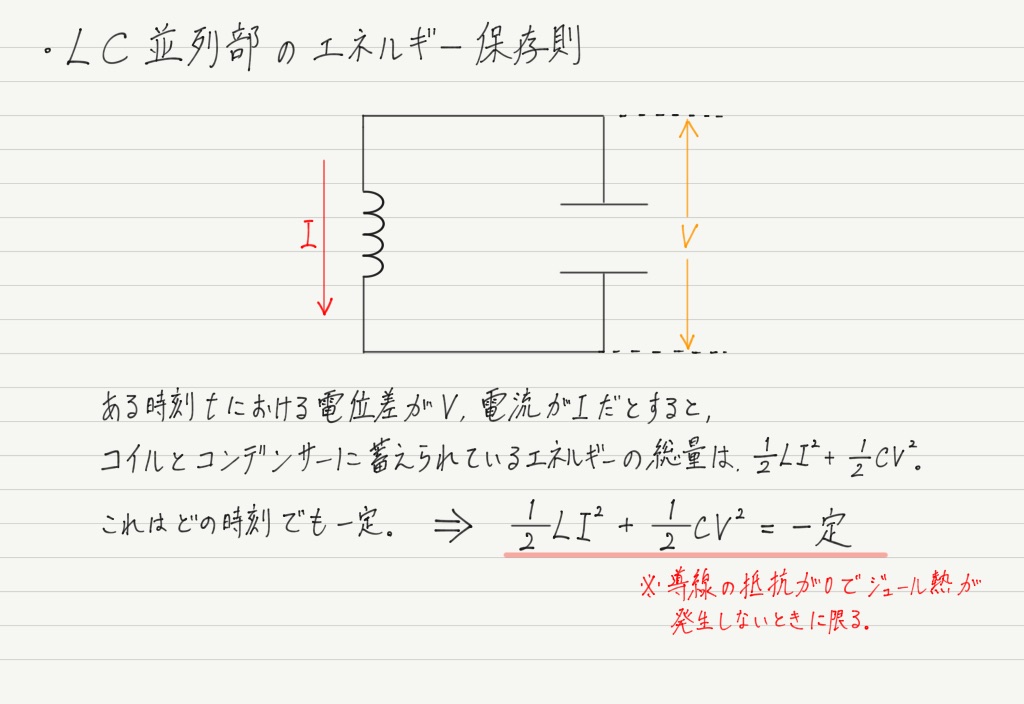
また,LC並列部は電源とは独立しているため,電源は仕事をしません。
電気振動ではコイルとコンデンサー間ですべて完結しているため,エネルギー保存則が成り立ちます!
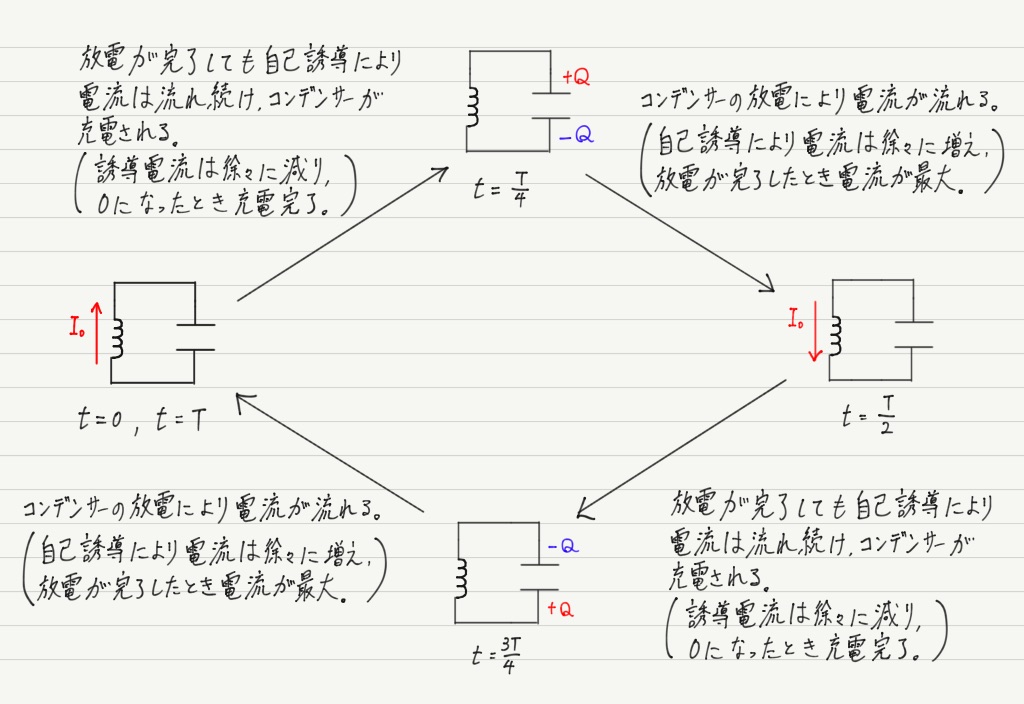
イメージで理解する電気振動
上の説明では式を使って電気振動が起こることを示しましたが,コイルの自己誘導とコンデンサーの充電・放電を使って説明することも可能です。
コイルやコンデンサーのはたらきがしっかり理解できていれば,決して難しい現象ではありません!
今回のまとめノート
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください!
次回予告
いよいよ電磁気分野の最終講を迎えます。
電磁気学によってその存在が明らかにされた,電磁波について理解を深めましょう。