基本的な用語の解説が済んだところで,いよいよ交流電源をつないだ回路の話に突入します。
電気回路によく用いられる基本的な部品は,抵抗,コイル,コンデンサー。
これら3つの部品の交流電圧に対する挙動について,ひとつずつ学んでいきましょう!
電圧と電流の位相のずれ
本題に入る前に交流回路を扱う上で不可欠かつ,直流回路にはまったくない概念を紹介しておきましょう。
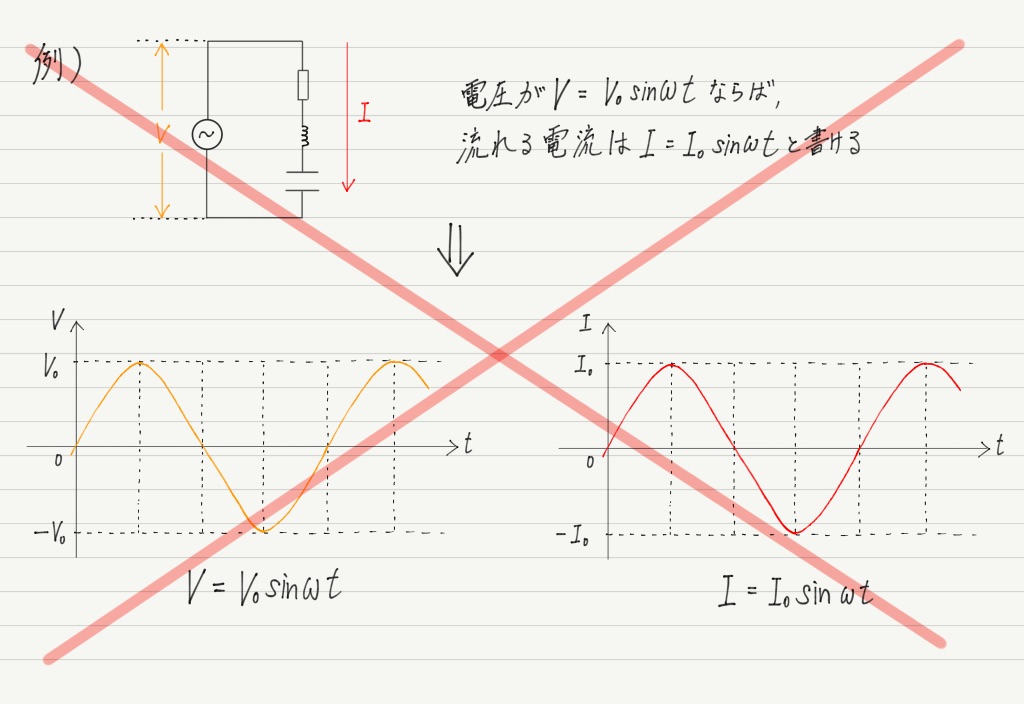
前回までに学んだとおり,交流電圧や交流電流は三角関数を用いて表されます。
三角関数の “角度” にあたる部分を物理では「位相」と呼びますが,交流回路ではこれが重要!
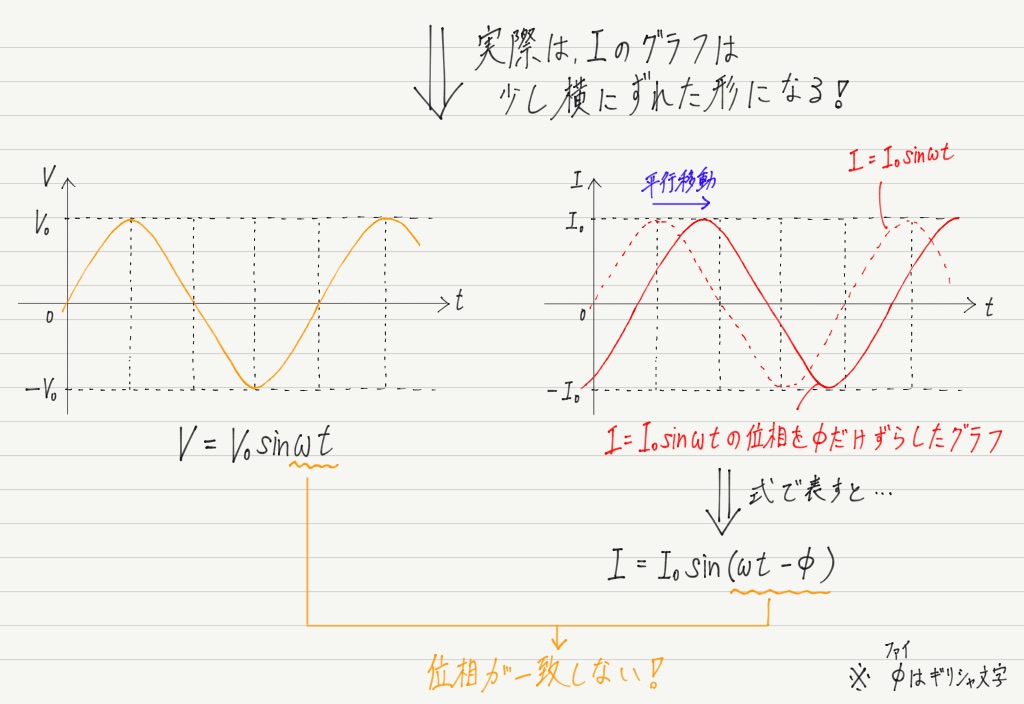
抵抗やコイル,コンデンサーなどの部品を適当につなぎあわせて交流電圧をかけると,かけた電圧と流れる電流の位相は一致しないことがほとんどだからです!
※ この図のように,グラフが右にずれている(φ>0)とき,“電圧に比べて電流の位相がφ遅れている” ,逆に左にずれている(φ<0)ときは,“電圧に比べて電流の位相がφ進んでいる”という。
このように,「位相がどれだけずれている(遅れている or 進んでいる)か」が交流回路では大事になってきます。
電圧や電流の大きさを求めるだけだった直流回路に比べるとややこしいですね…
ただし,本当にややこしいのはいろいろ部品をつないだ場合であって,「抵抗1個だけ」とか,「コンデンサー1個だけ」とか,「コイル1個だけ」なら簡単!
というわけで,まずは「部品1個だけ回路」の性質を紹介していきます。
抵抗と位相のずれ
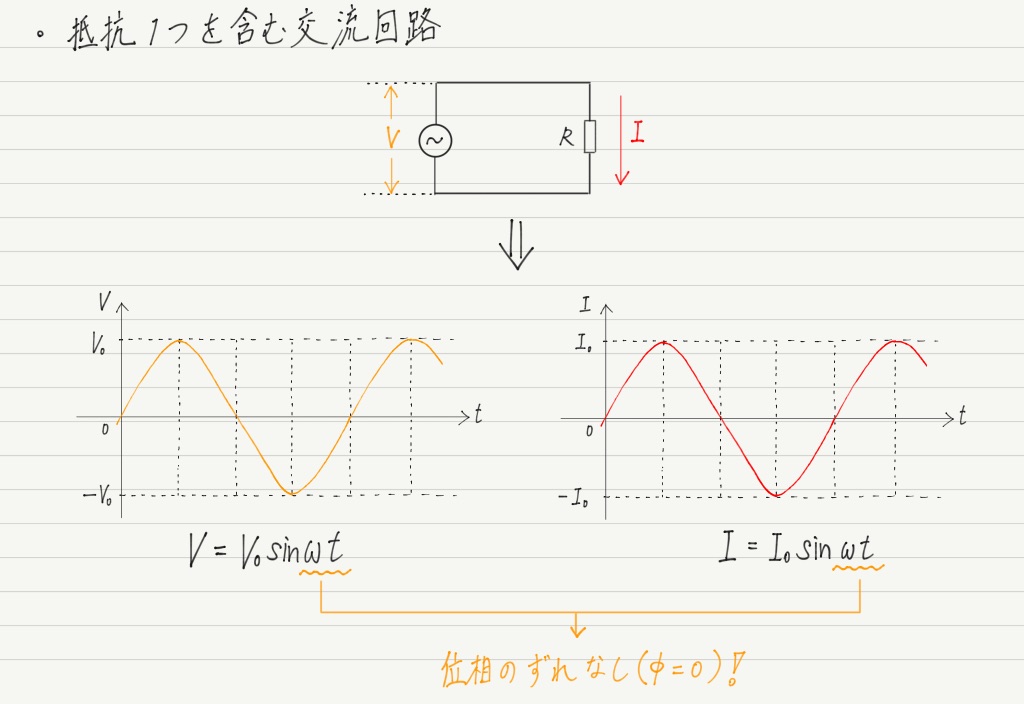
今回のテーマは「抵抗1個だけ回路」。
ダラダラとした説明はしません! 結果だけ覚えてください。
まずは位相のずれですが,抵抗の場合,電圧と電流の位相は同じ。 まったくずれません。
「ずれが大事」と言った直後だけに肩透かしを食った気分かもしれませんが,抵抗とはそういう特徴をもつ部品なのです。
まぁ,わかりやすくていいじゃない。
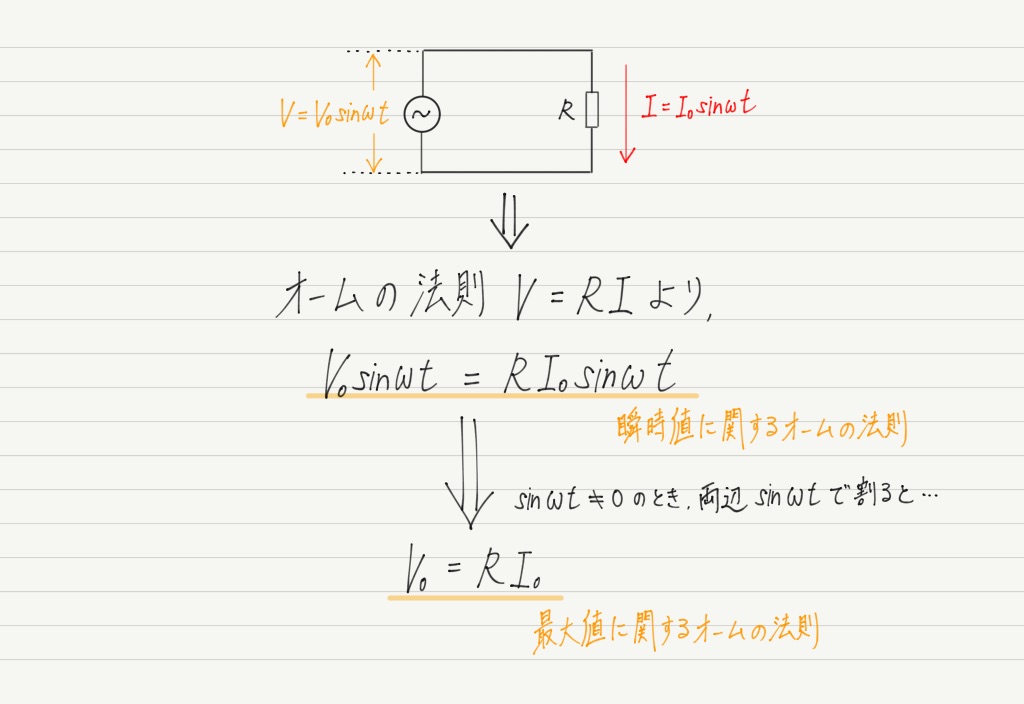
電流と電圧の関係
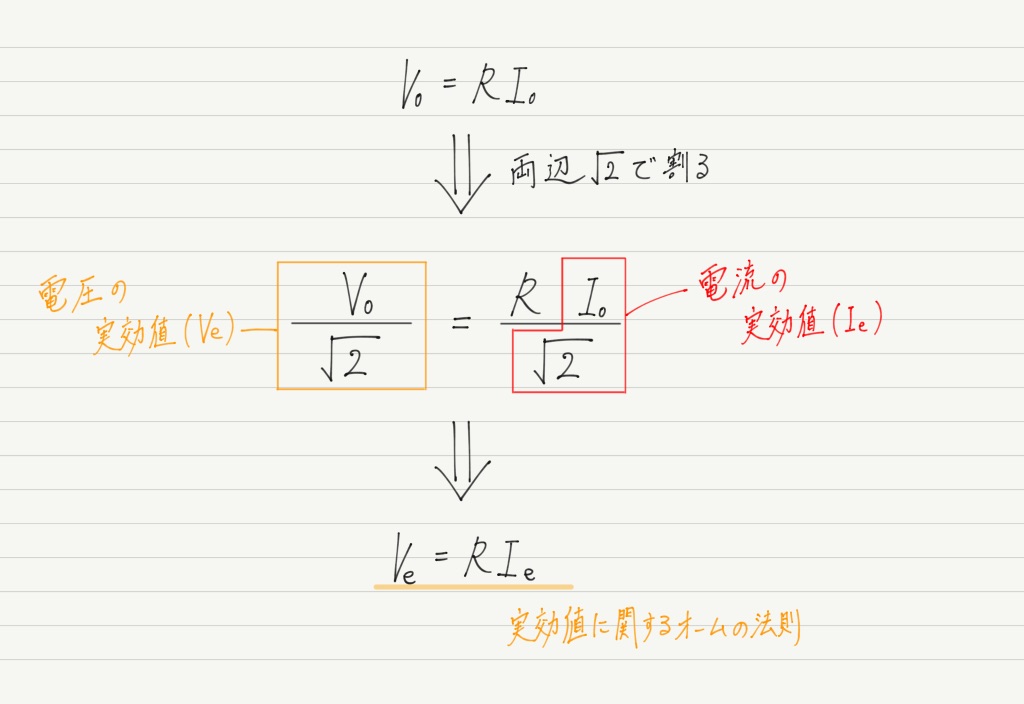
交流回路であっても,抵抗に関しては直流同様にオームの法則が成り立ちます。
もちろん実効値でも成り立ちます。
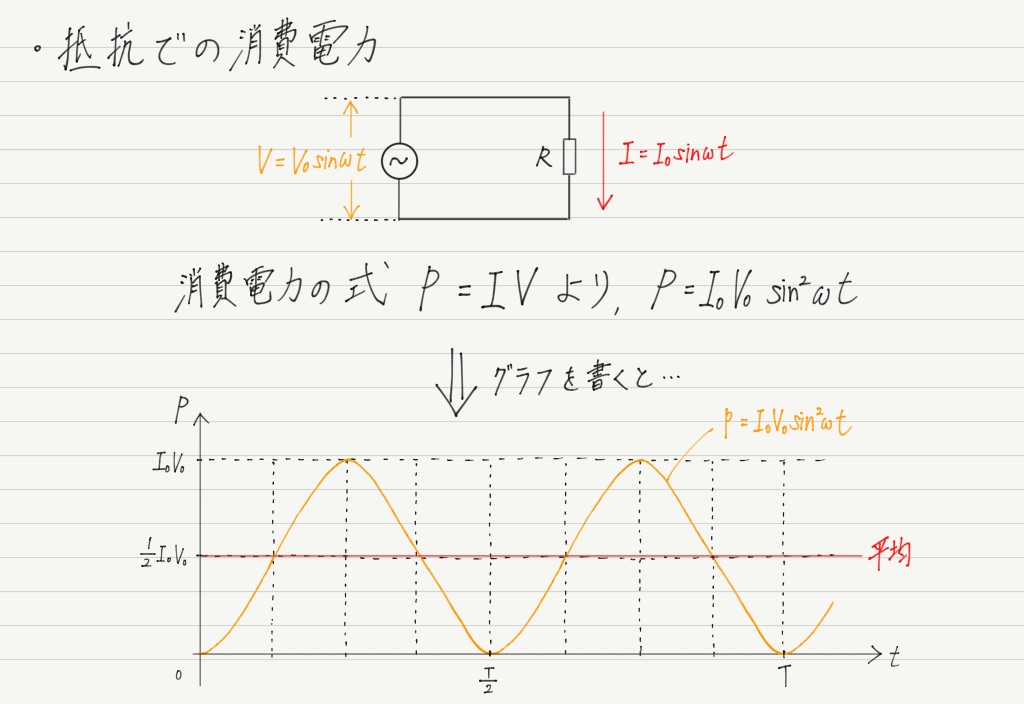
消費電力の平均
抵抗での消費電力の話は前回すでに学習済み。 一応書いておくと,
未読 or 忘れてしまった人はこちら ↓ で確認してください。
今回はこれで終了。
抵抗のみを含む交流回路は,電圧と電流に位相のずれがないためにあまり目新しさがありませんでしたね。
特に実効値を用いた場合には,オームの法則も消費電力(の平均)も,直流回路のときとまったく同じ式になっています!
今回はまとめノートはありません(コイルとコンデンサーが終わったときにひとまとめにして書く予定です)が,時間に余裕がある人はぜひ問題演習にもチャレンジしてみてください!
次回予告
次回は「コイル1個だけ回路」を扱います!