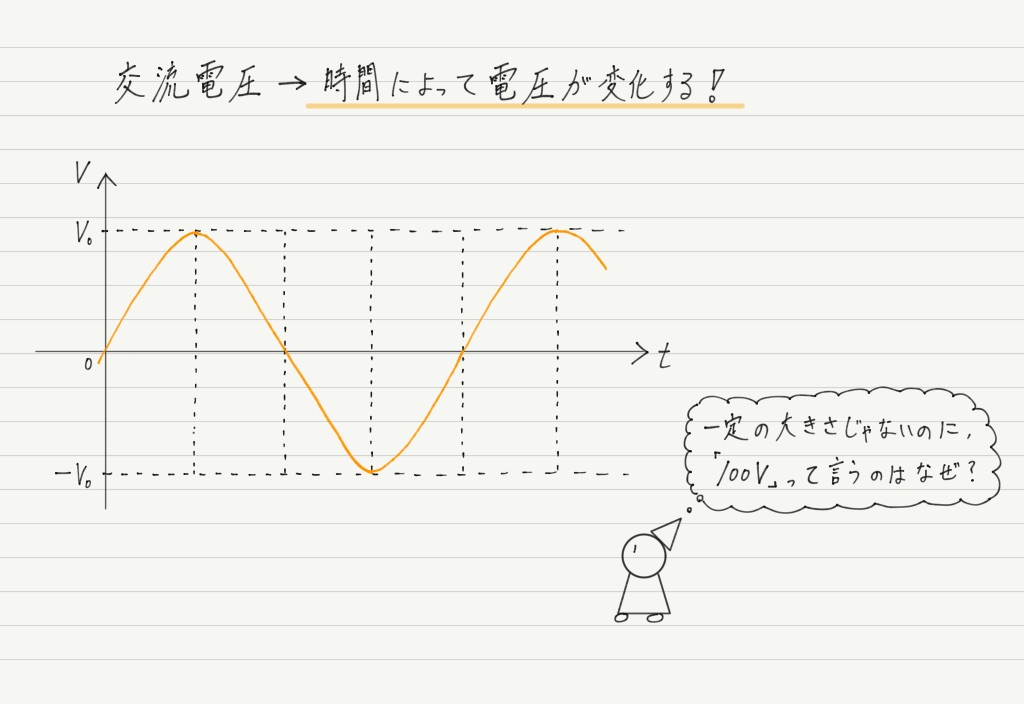
「家庭用電源の電圧は100V」というのはどこかで聞いたことがると思います。
しかしこれ,よくよく考えてみるとおかしいですよね?
だって,家庭に送られている電気は交流だもの!!
今回はこんな些細な(?)疑問に答える回です。
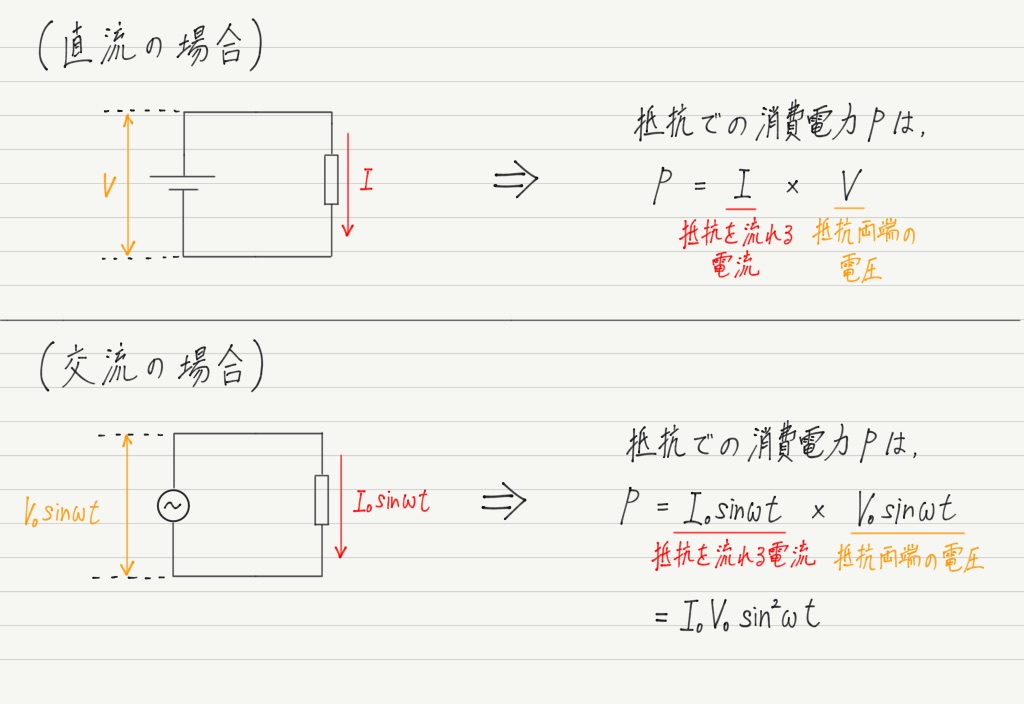
抵抗の消費電力(交流Ver.)
この疑問に答えるためのヒントはズバリ,消費電力。
抵抗に交流電圧をかけた場合の消費電力を求めてみましょう。
交流の方には時間 t が含まれていますが,交流は直流とちがって電圧や電流が時間とともに変化するので,消費電力も時間の経過とともに変化するのは当たり前。
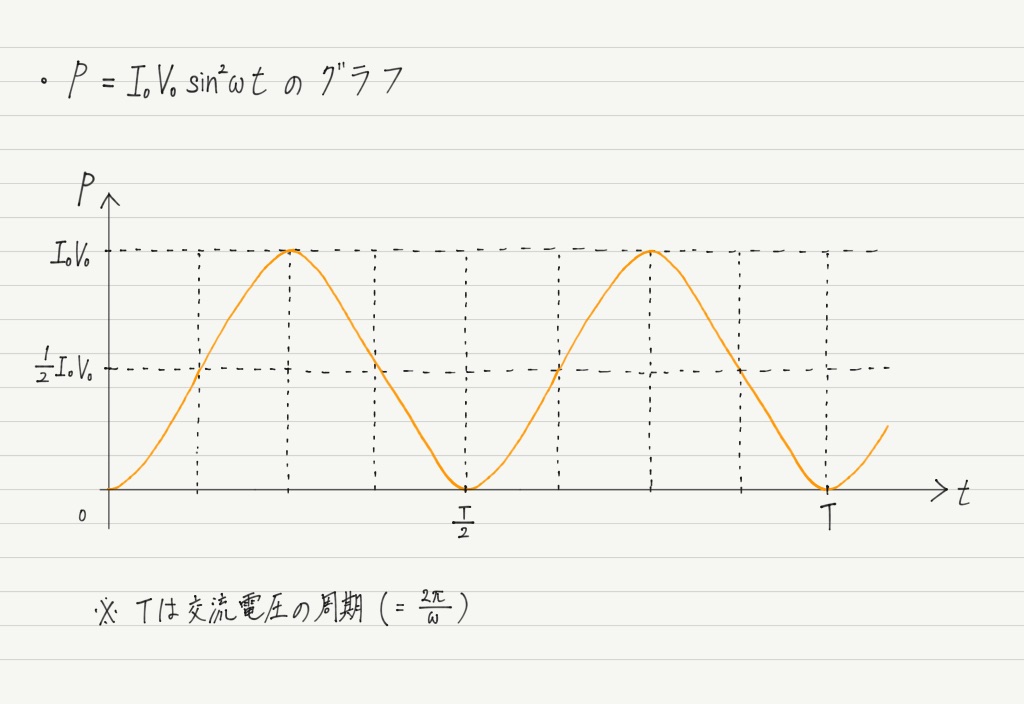
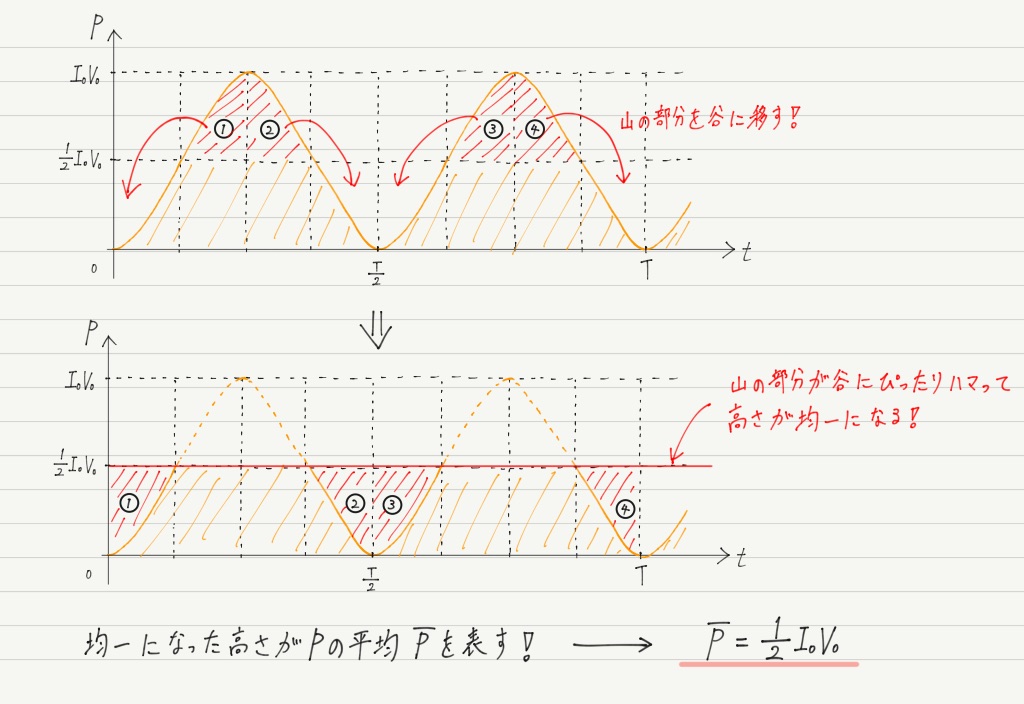
このPの式をグラフで表すと以下のようになります。
「ふーん,こういうグラフなのかぁ」って感じで軽くスルーして構いませんが,本当にこのグラフになるのか半信半疑の人は,Pの式に半角の公式を適用して式変形するか,微分して増減表をつくってみてください。
確かにこのグラフになることが確かめられるはずです。
消費電力の平均値
しつこいですが,みなさんの家に送られている電気は交流なので,各家庭での消費電力も上のグラフのように表せます。
時刻によって,0だったり,最大値だったり,その中間の値だったり…
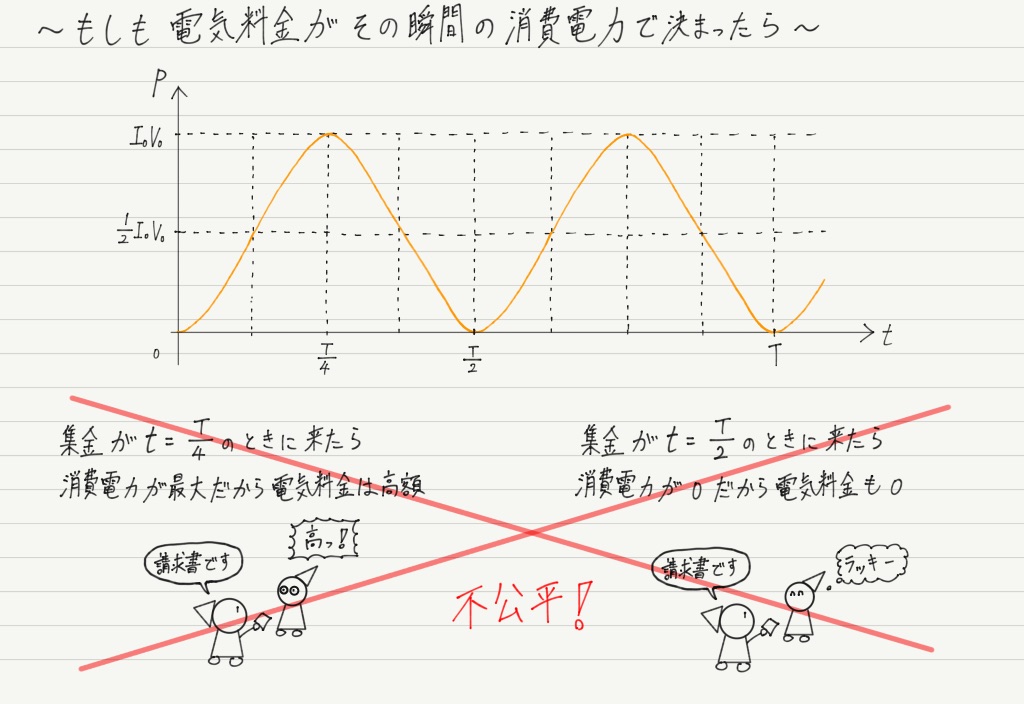
…はて? そうなると1つ問題が生じます。 各家庭の電気料金はどうやって算出すればいいでしょうか?
電力会社の人が家のメーターをチェックしに来た時間によって変わる??
んなわけない。
消費電力が0と最大値の間を上下してるんだから平均すればいいじゃない。
グラフの形がシンプルなので,消費電力の平均値はわざわざ計算しなくても図形的に求められます。
ほら簡単 !
(電気料金はそもそも消費電力じゃなくて消費電力“量”だろ!っていうツッコミはナシで笑)
実効値という考え方
思いっきり話が逸れているようにみえますが,もう少しの辛抱。
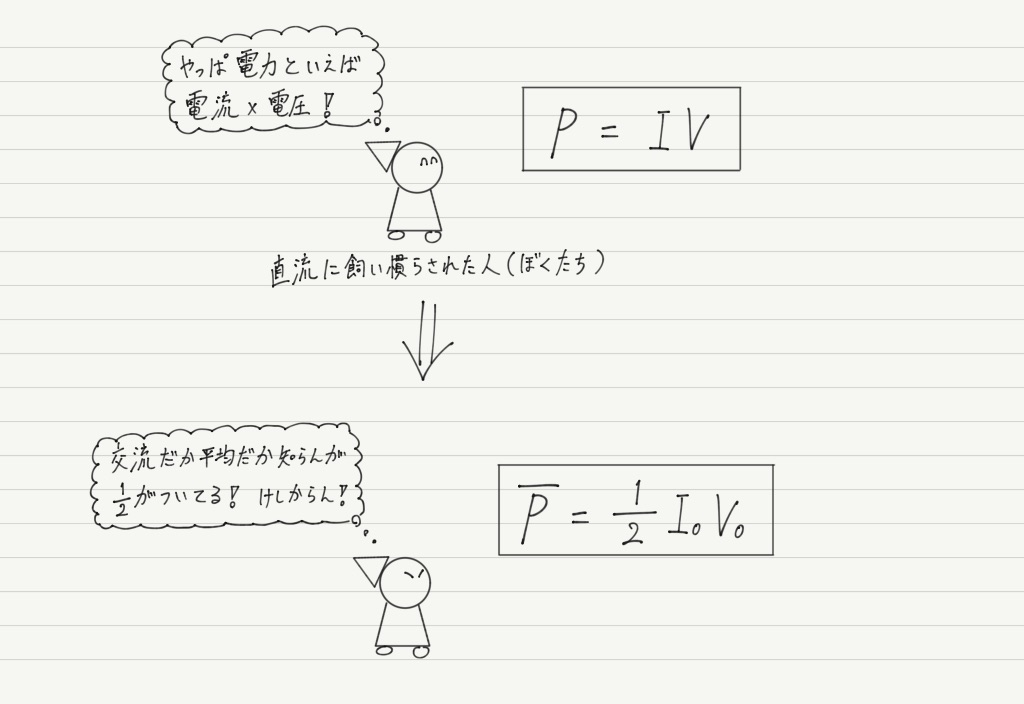
消費電力の平均値が求められたのはいいけど,これまで直流ばかりやってきた我々からするとこの式ちょっとモヤモヤしません?
交流だろうが平均だろうが,消費電力である以上は,「電流 × 電圧」という形であってほしいわけですよ!
(すごいわがまま笑)
そこで,次のような置き換えをしてみます。
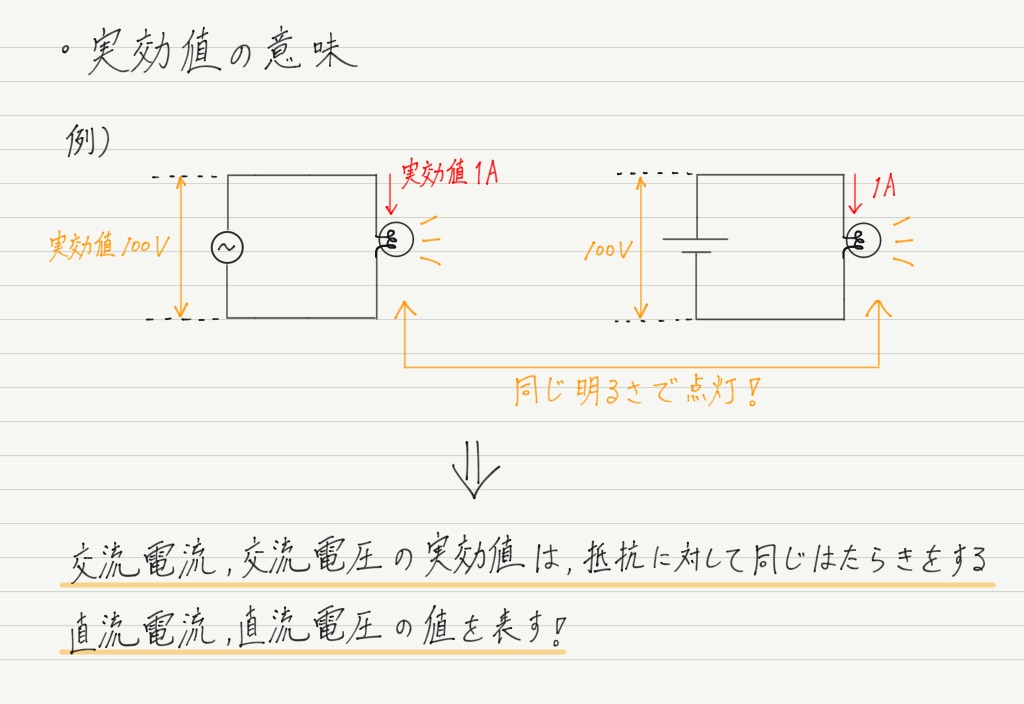
このように実効値を使うと,交流なのに直流と同じように消費電力(の平均)を表せます! これは便利!!
…え? こじつけじゃないかって?
うーん,確かにこの説明だけ聞くと,実効値というものを無理矢理つくり出した感がすごいですよね…
でもご安心を。 ちゃんと物理的な意味もあります。
直流に比べると交流はどうしてもイメージしにくいのですが,そのギャップを少し埋めてくれるのが実効値なのです!
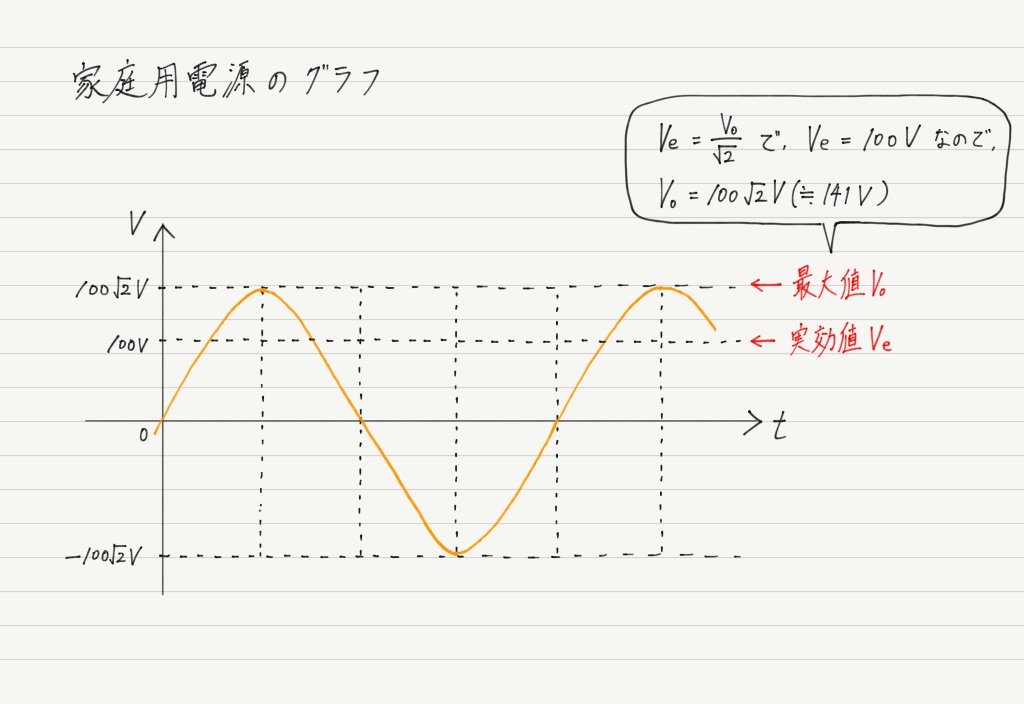
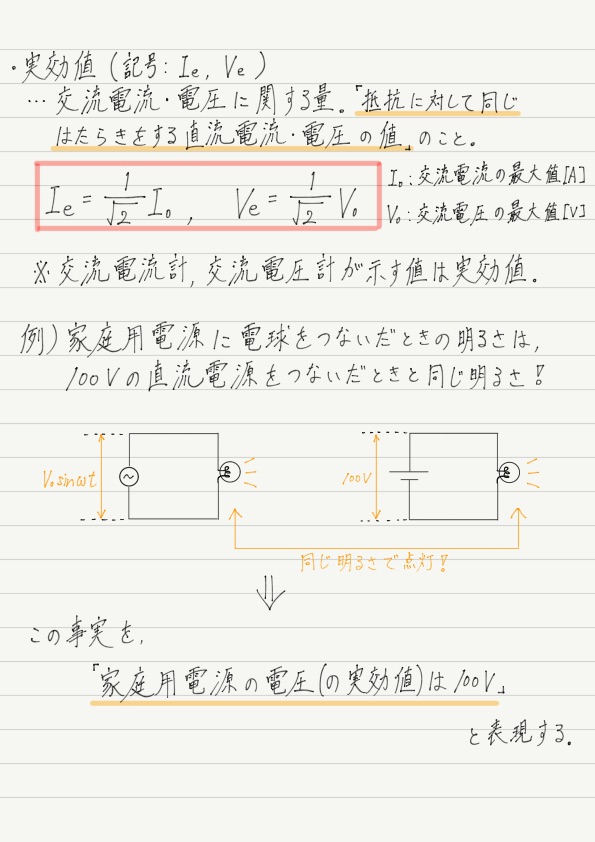
…もう察したかと思いますが,冒頭の疑問に対する答えは,「家庭用電源の電圧は100V = 実効値が100V」ということになります。
今回のまとめノート
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。
次回予告
交流分野の最終目標は回路の問題が解けるようになること。
手始めに抵抗を含む交流回路から学習しましょう。