電磁誘導まだまだ続きます。
「回路は1回巻きのコイルとみなせる」みたいなやつじゃなく,今回は正真正銘のぐるぐる巻きのコイルを扱っていきます!
電磁誘導(特に誘導起電力の向き)について不安がある人は,過去記事で復習してからこの記事にトライしてください。
回路内のコイルによる電磁誘導
今回のテーマは回路内にあるコイル。
回路の中に組み込まれているということは,スイッチのON・OFFによってコイルに電流が流れたり流れなかったりします。
さて,コイルに電流が流れると,その電流の大きさに比例した磁場がコイル内部に生じるのでした!
このことから,回路のスイッチを操作してコイルに流れる電流が変化すると,それに伴って内部の磁場も変化することがわかります。
するとどうなるか。
コイルは内部の磁場の変化を嫌う(あまのじゃく!)ので,電磁誘導をすることになります!!
それでは,レンツの法則のところでやったのと同様に,コイル内部の磁場の増減に注目して誘導電流の向きを考えてみましょう。
レンツの法則と右ねじの法則がしっかり理解できていれば大丈夫だと思います。
ところでこの電磁誘導,よく考えるとちょっとややこしいことになっていて,
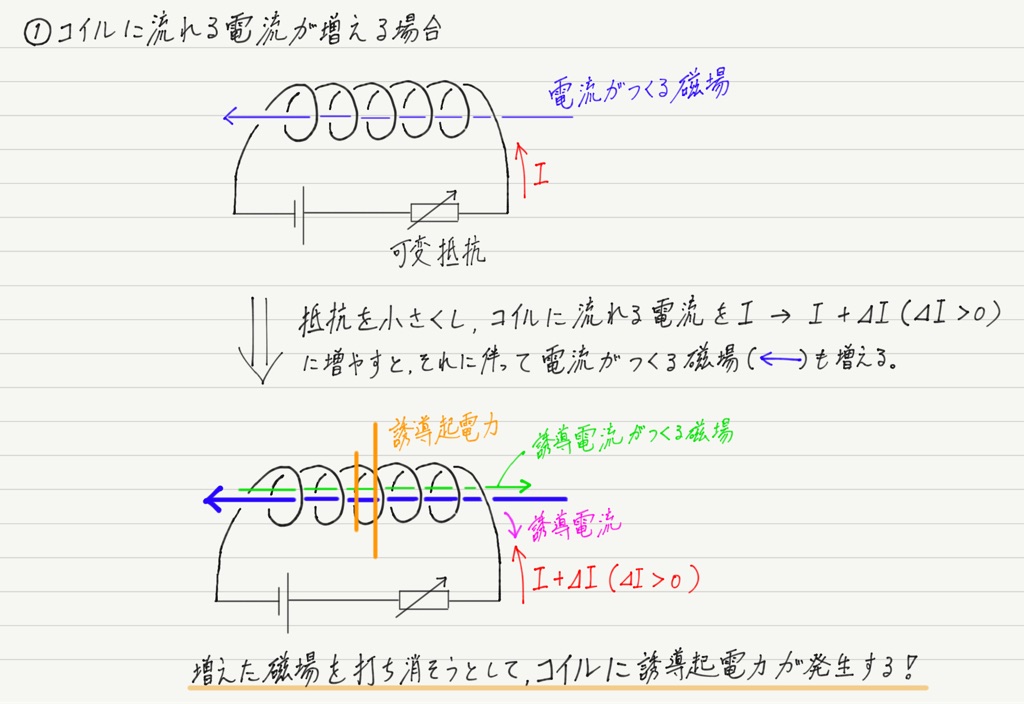
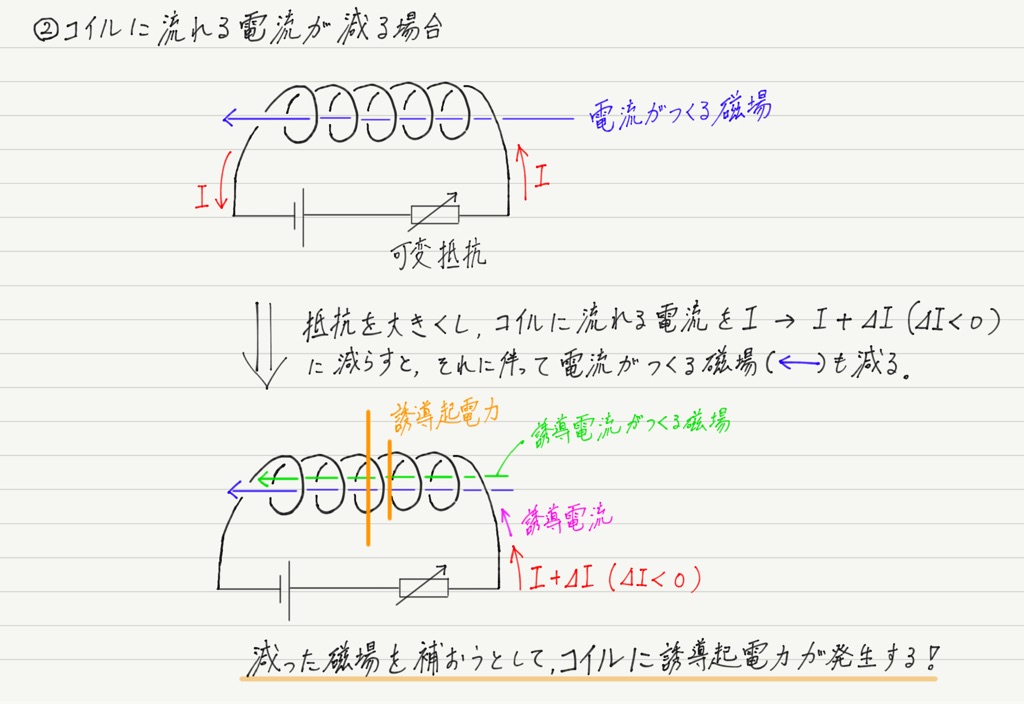
コイルに流れる電流が変化する。
↓
コイルがつくる磁場が変化する。
↓
コイルが磁場の変化を嫌って,電磁誘導を起こす。
…ん? コイルは自分で自分の磁場を変化させておきながら,その変化を嫌うってこと?
まさにそのとおり。
例えるなら街中で一人で腹を立てて,一人で怒鳴り散らしてるやべぇオッサン(たまにいるよね)。
コイルのこのような電磁誘導は自分の変化を自分で打ち消そうとしていることから,自己誘導と呼ばれます。
自己誘導起電力の大きさ
自己誘導も電磁誘導の一種なので,「誘導起電力をつくって誘導電流を流す 」ことに変わりはありません。
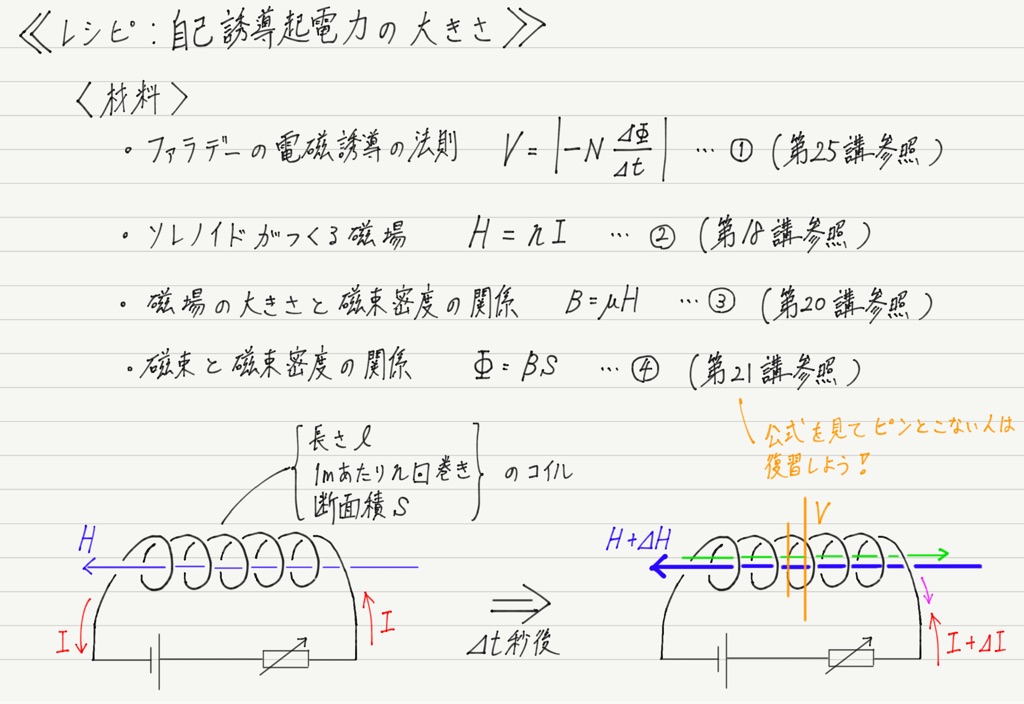
せっかくなので自己誘導による誘導起電力(自己誘導起電力)の大きさを求めてみましょう。
これまでに出てきた公式たちのオンパレード!
自己誘導起電力の大きさを求めるというより,公式を駆使してファラデーの電磁誘導の法則を式変形しただけ。
ですが自己誘導起電力の大きさVを,そもそもの原因である電流の変化⊿ Iを用いて表すことに成功したので,非常に使いやすい形になりました! やったね!
そして比例定数として現れた自己インダクタンス Lですが,式を見てわかるとおり,
Lが大きいコイル=自己誘導起電力Vも大きい → めっちゃあまのじゃく
Lが小さいコイル =自己誘導起電力Vも小さい → そんなあまのじゃくじゃない
と解釈できます。
要するにLは,「そのコイルがどれぐらいあまのじゃくか」を測る数値なのです。
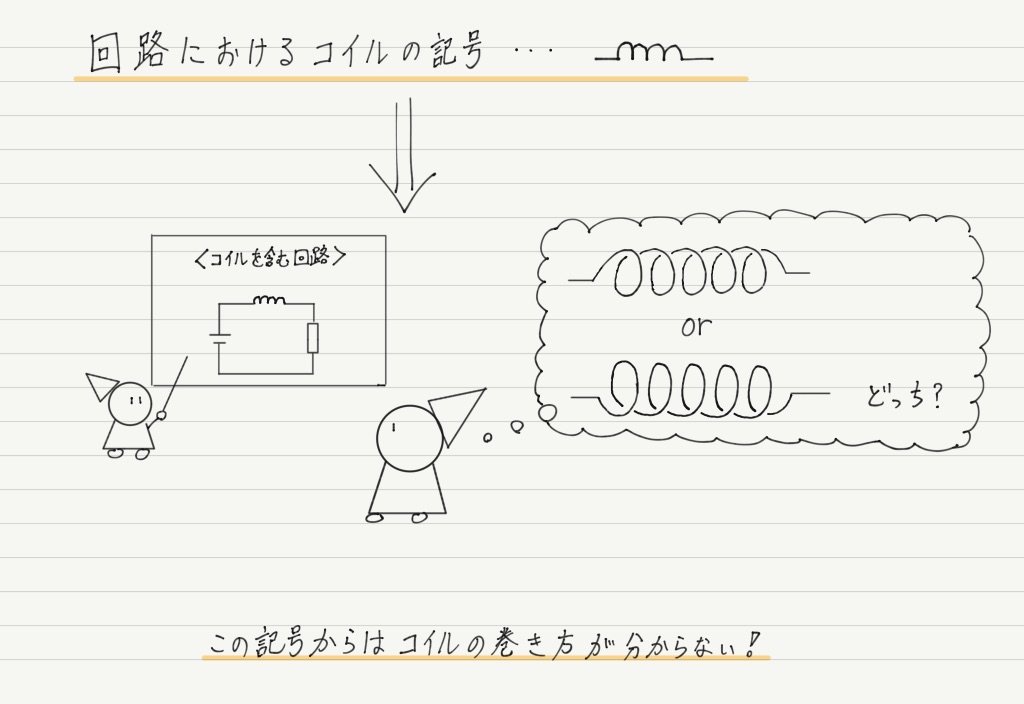
回路の問題では右ねじの法則が使えない!?
このあと回路の問題をやるのですが,その前にこれを見てください。
これはまずいのでは…?
巻き方がわからないと右ねじの法則が使えない → 磁場の向きがわからない → 誘導電流の向きがわからない!!
という事態になってしまいます。 わぁ大変。
…というのはウソで,実は誘導電流の向きは右ねじの法則を使わなくてもわかるのです。
なぜなら,コイルのあまのじゃくな性格は内部の磁場だけでなく,流れる電流に対しても発揮されるから。
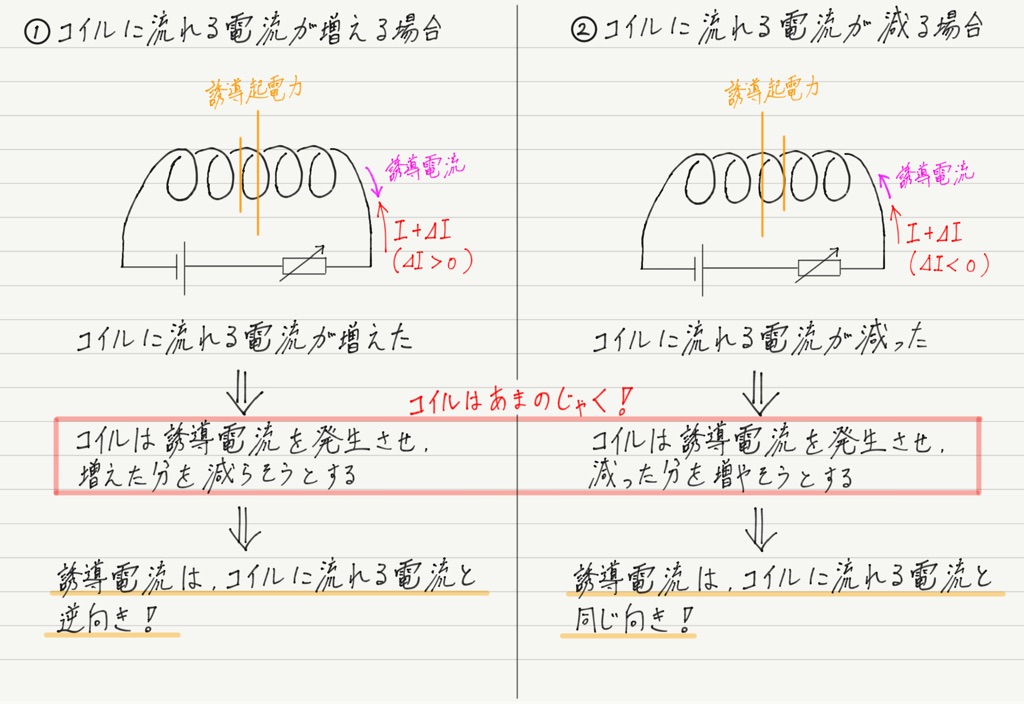
さっき挙げた例を,流れる電流の向きに注目してもう一度見てみましょう。
ね? 磁場や右ねじの法則なんか使わなくても,誘導電流の向きが求められたでしょ?
これならコイルがどっち巻きかわからなくても平気!
実際の回路の問題を解く上で必須の考え方です。
コイルを含む回路の原則
いよいよコイルを含む回路の話に入っていきます。
が,その前に以前学習したコンデンサーを含む回路を思い出してください。
コンデンサーとコイルでは役割がまったくちがうのですが,回路の中での振る舞いには少し似たところがあります。
それは,スイッチを「操作した(入れた or 切った)直後」と「十分時間が経過したあと」ではたらきが変わるところ,そして,問題でその2パターンしか問われないところです!
(スイッチを入れて t[s]後どうなるか,という問題は出ない)
では,その2パターンそれぞれのはたらきについて確認していきましょう。
おさらいですが,
・コイルはあまのじゃくなので,誘導電流をつくり出して,電流の変化を妨げようとすること。
・最初は妨げようとするが,徐々に変化を受け入れ,最終的には自己誘導しなくなること。
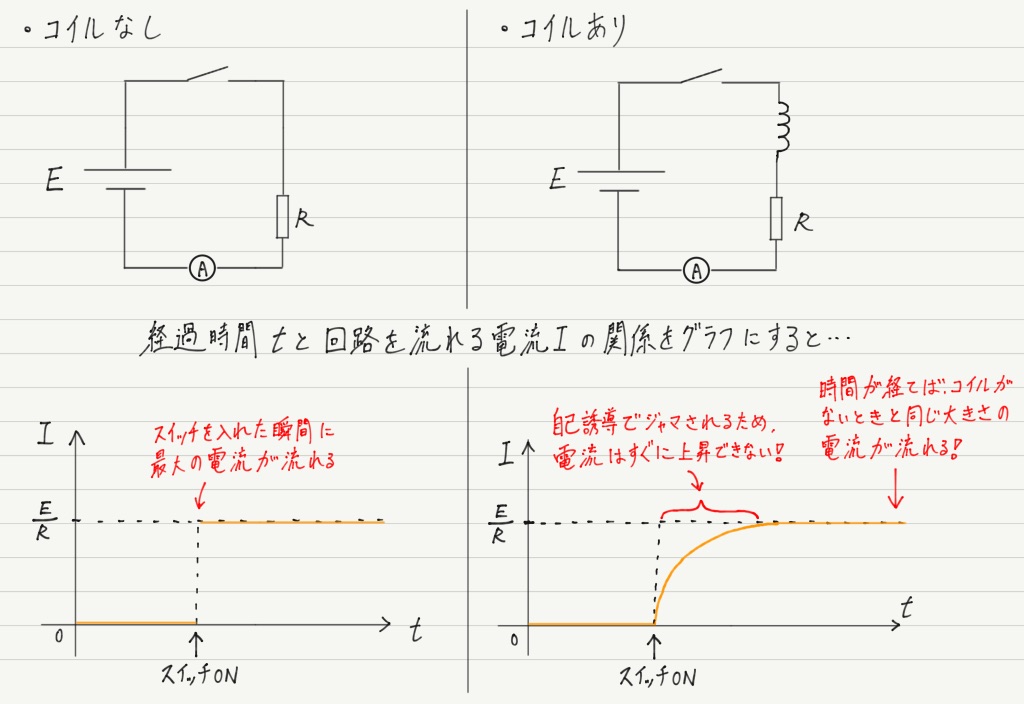
この2点を踏まえた上で,以下の回路とグラフをご覧ください! まずはスイッチONの場合。
スイッチONして電流が流れようとしたときに,自己誘導によってブレーキがかけられるイメージ。
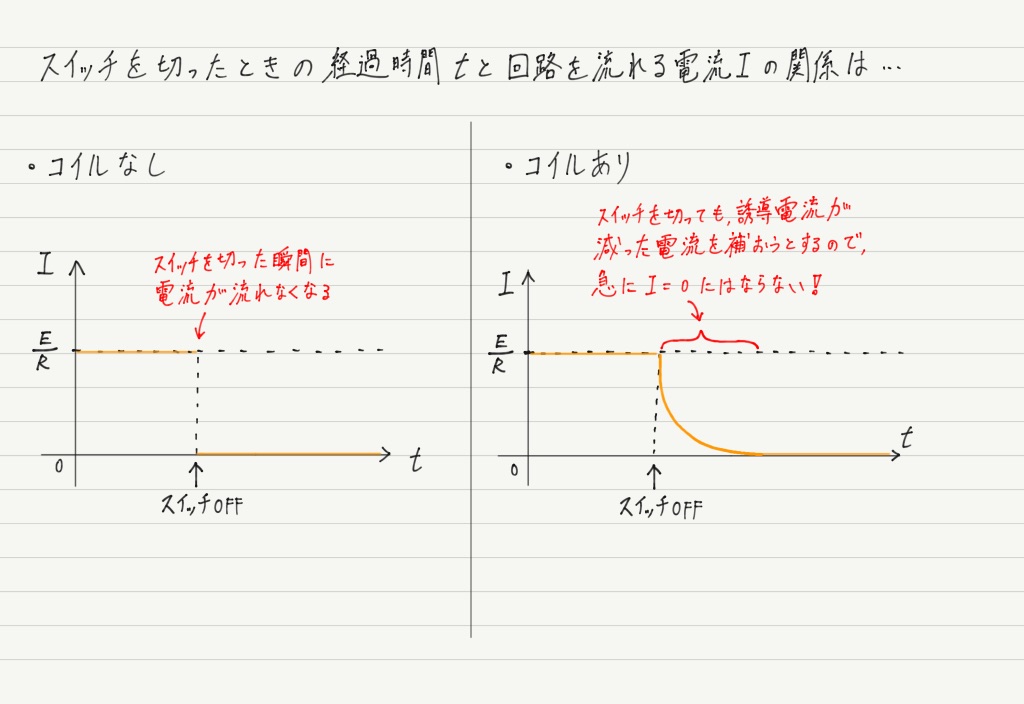
次にスイッチOFFしたときのグラフを見てみましょう。
スイッチOFFの場合も自己誘導の影響で,グラフはゆるやかなカーブです。
まとめると,コイルを含む直流回路の問題では,
・スイッチを操作した直後 → 自己誘導により電流は急激に変化できない → 流れる電流はスイッチを操作する直前と同じ!
・スイッチを入れて十分時間が経過 → コイルの自己誘導は終わっている → コイルは導線とみなせる
ということになります。
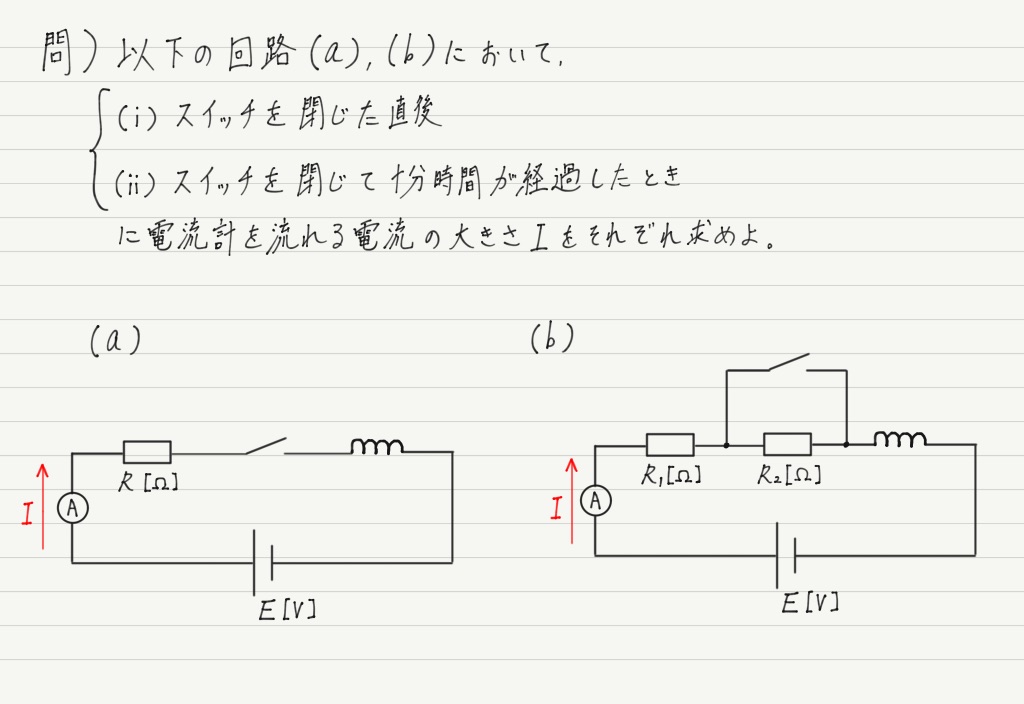
例題
最後に例題を解いて理解を深めましょう。
解答はこの下にありますが,まずはチャレンジ!
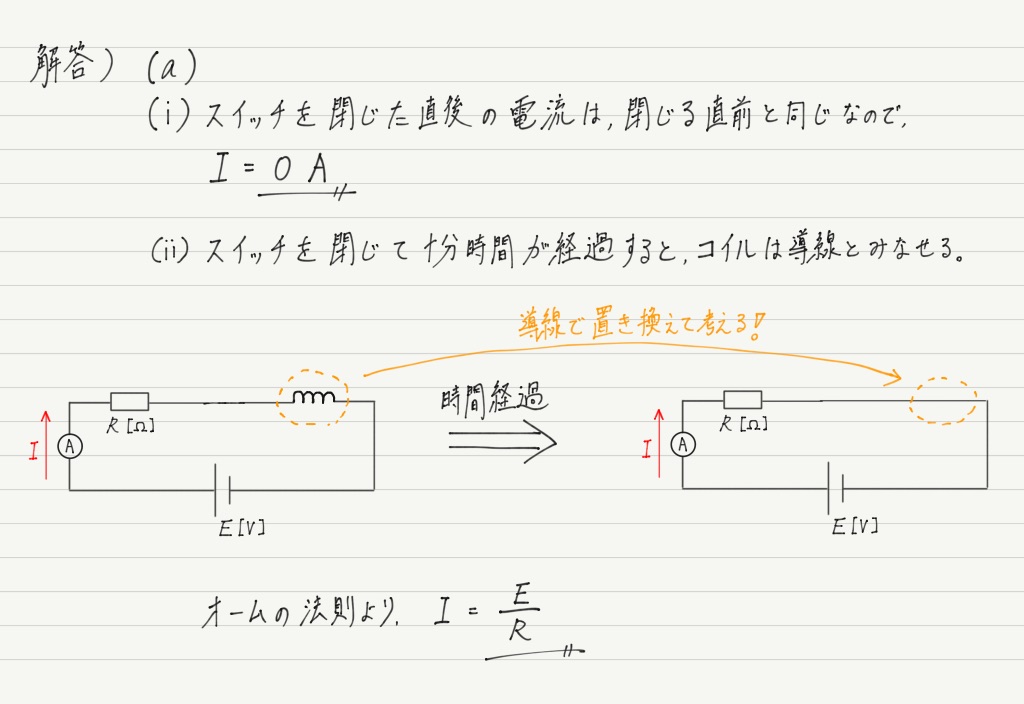
できましたか? では答え合わせしましょう!
“覚えやすさ” に騙されるな!
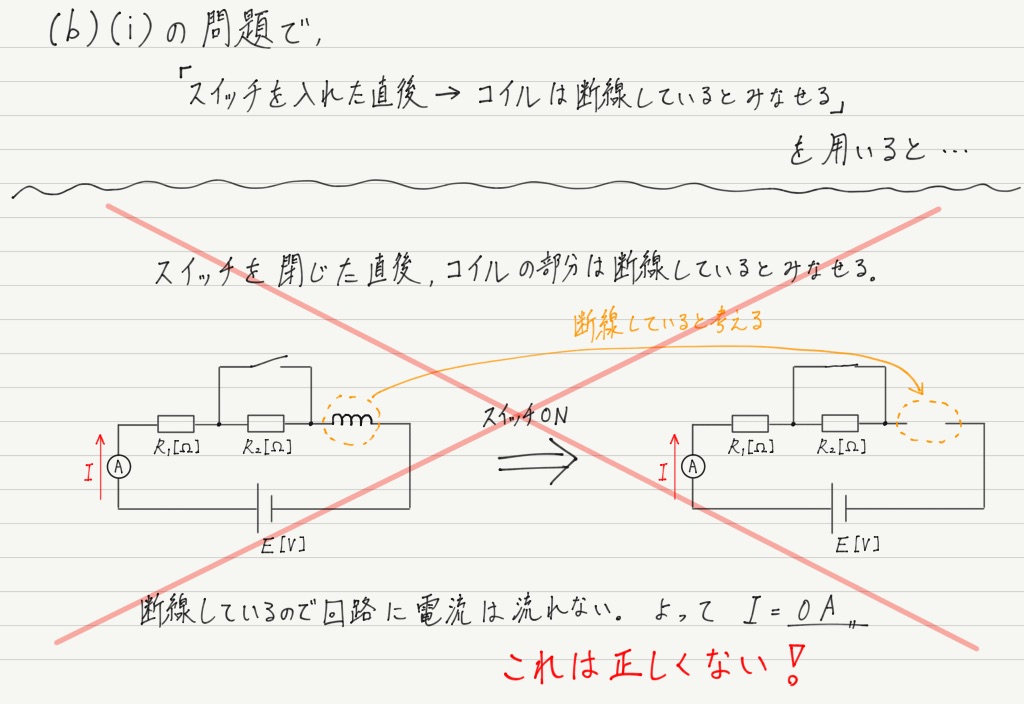
時折,「スイッチを入れた直後のコイルは,断線しているとみなせる」という解説を見かけます。
なるほど,これは覚えやすく感じます
が,ちょっと待ってください。 実はその覚え方だと上の例題の(b)の問題が解けません!!
「スイッチを入れた直後 = 断線と同じ」が通用するのは,はじめコイルに電流が流れていないとき限定です(最初に流れていなければ,スイッチON直後も流れないので断線しているのと同じ)。
覚えやすさにつられて本質を見失わないようにしましょうね!
今回のまとめノート
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。
次回予告
コイルの性質からはいろいろな応用が見えてきます。
たとえばコイルを2つ使ったら何が起こるでしょう?