電流を流すと，その周囲に磁場が生じることを前回学習しました。
では，はじめから磁場が存在しているところで電流を流すと何が起こるでしょうか？
フレミング左手の法則
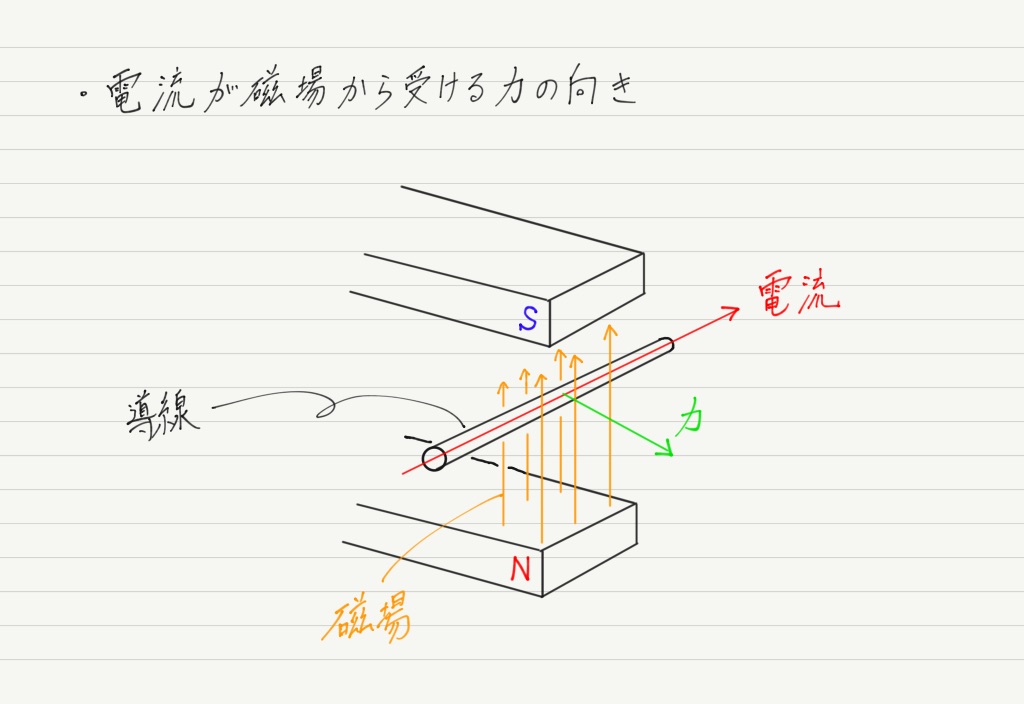
電流が磁場から力を受けることは中学校でならっているはずなので，いきなり結論から。
磁場中で電流を流すと，電流は磁場から力を受けます！
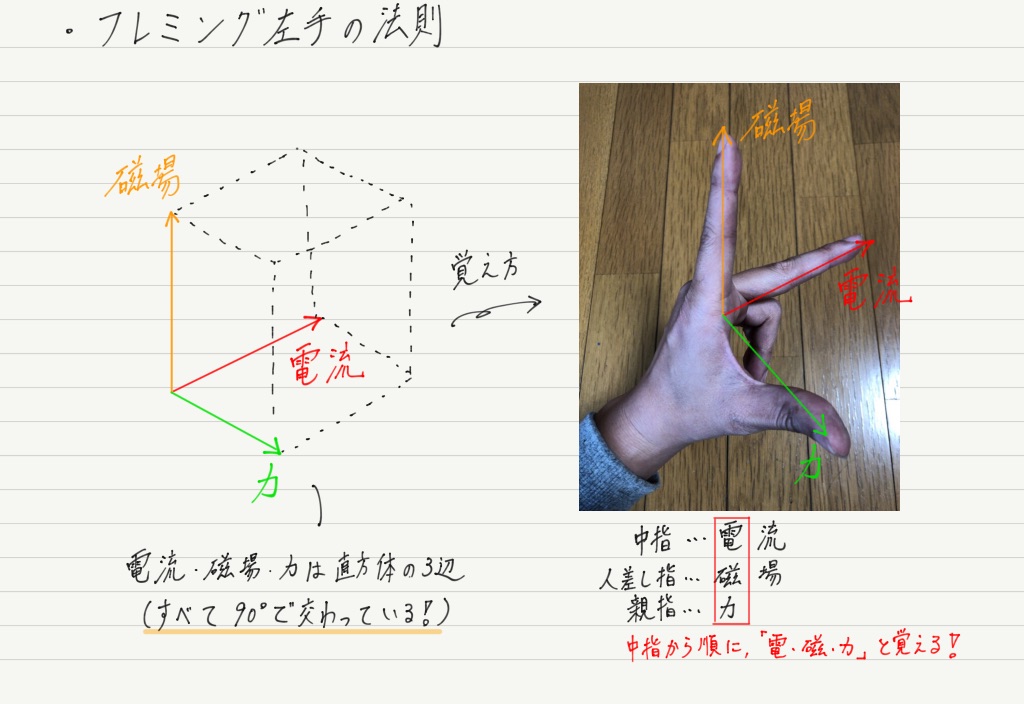
この現象はフレミング左手の法則として知られています。
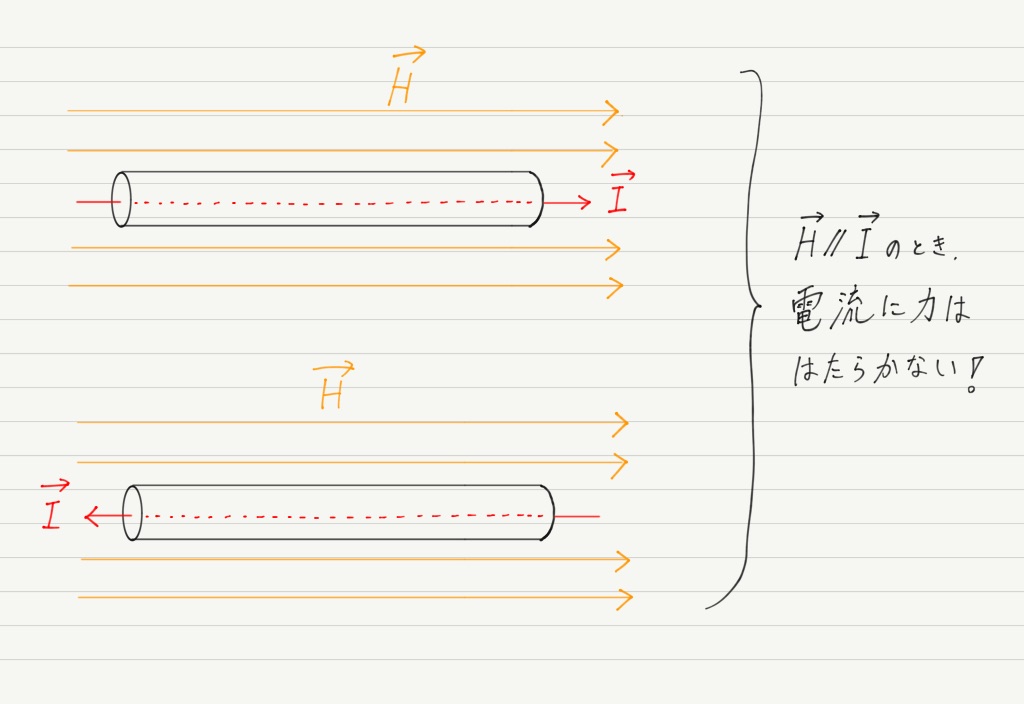
さて，電流が受ける力を考えるときは電流と磁場が直角であることが大前提です。 電流と磁場が平行の場合，電流は力を受けません！
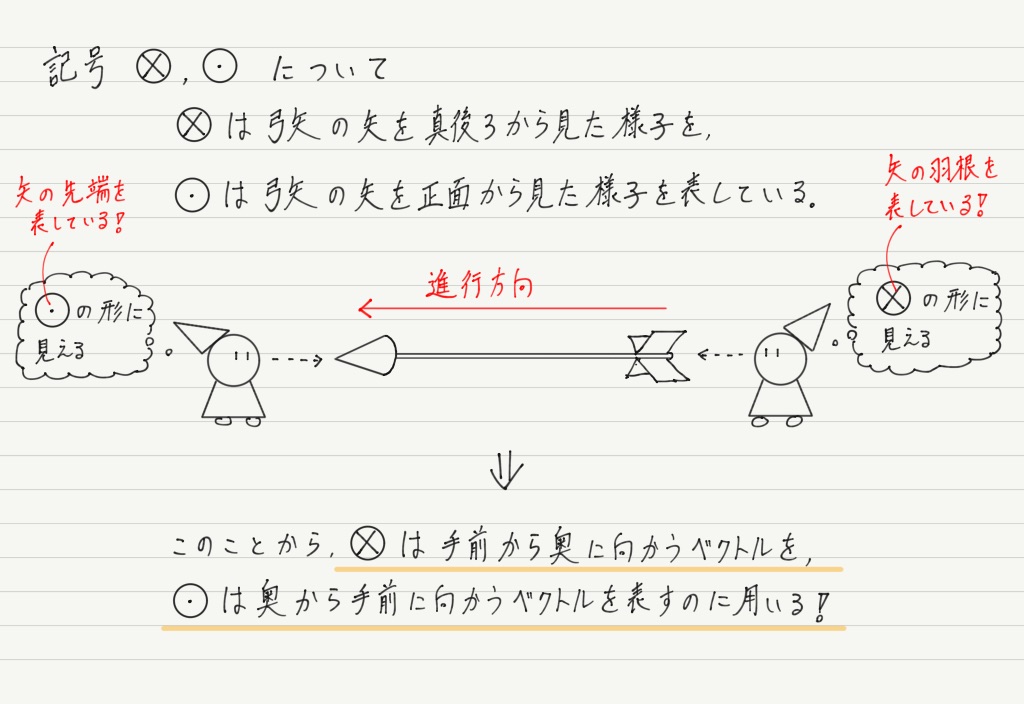
電流が受ける力の問題を解くときに困ったことがひとつあります。 それは，電流，磁場，力の向きの関係が立体的なので，図が書きにくいこと。
物理の問題で図を書くのはとても大切ですが，あまり時間はかけたくありません。
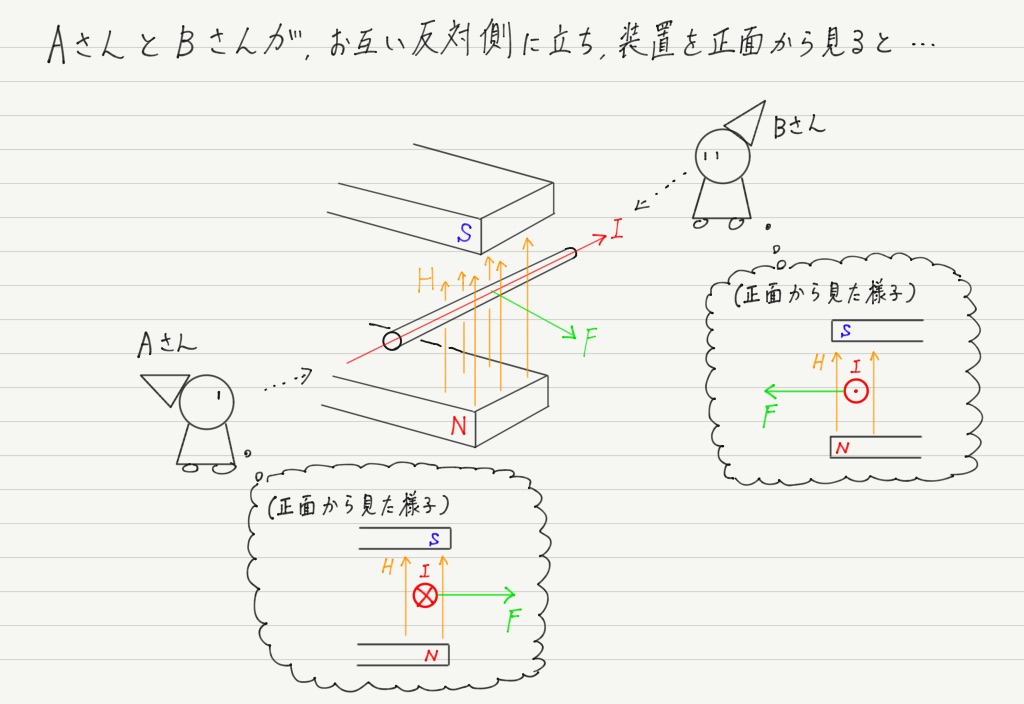
そこで，斜めから見た立体的な図ではなく，正面から見た図の書き方を紹介します！
この書き方はとても便利だし，問題中の図でも多用されるので，是非覚えてください！
電流が受ける力の大きさ
…と，ここまでは中学校の復習。 新しい知識が出てこないのは寂しいので，「電流は磁場から受ける力は何Nなのか」を計算できるようになりましょう！
もちろん公式を使って計算するのですが，それを紹介する前に，力の大きさが何に影響されるか考えてみてください。 なんとなくのイメージで構いませんが，
「強い磁場のほうが力が大きくなりそう」
「大きい電流を流したほうが受ける力も大きくなりそう」
…って気がしませんか？？
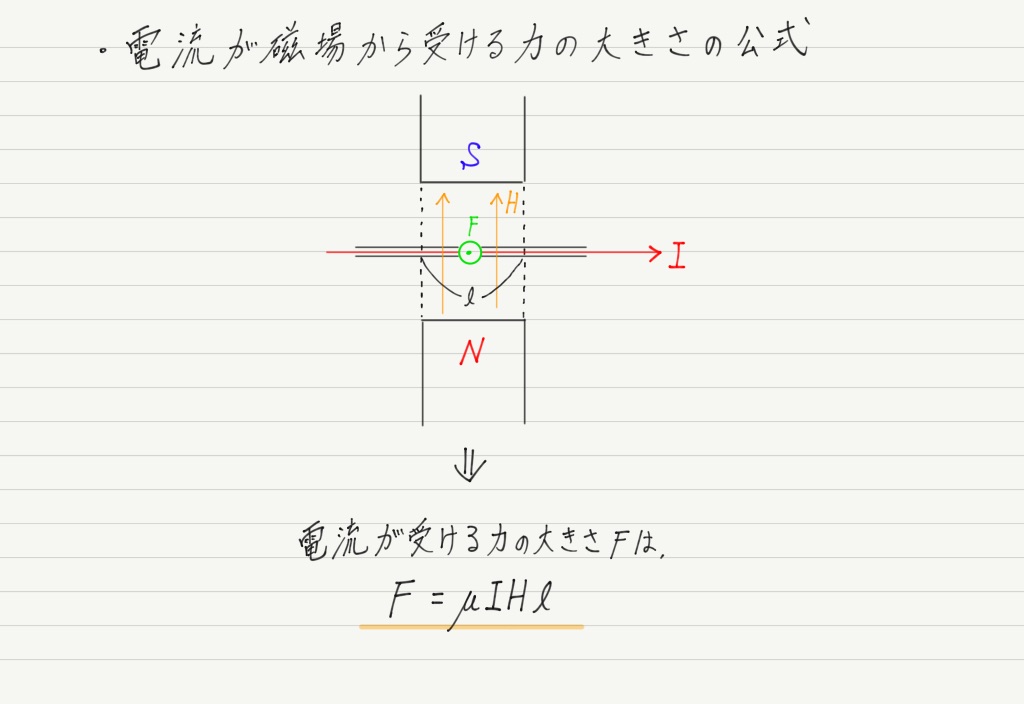
実はまったくその通りで，電流が受ける力の大きさは，電流の大きさと磁場の強さ，それから，磁場の中に含まれる導線の長さに比例します！
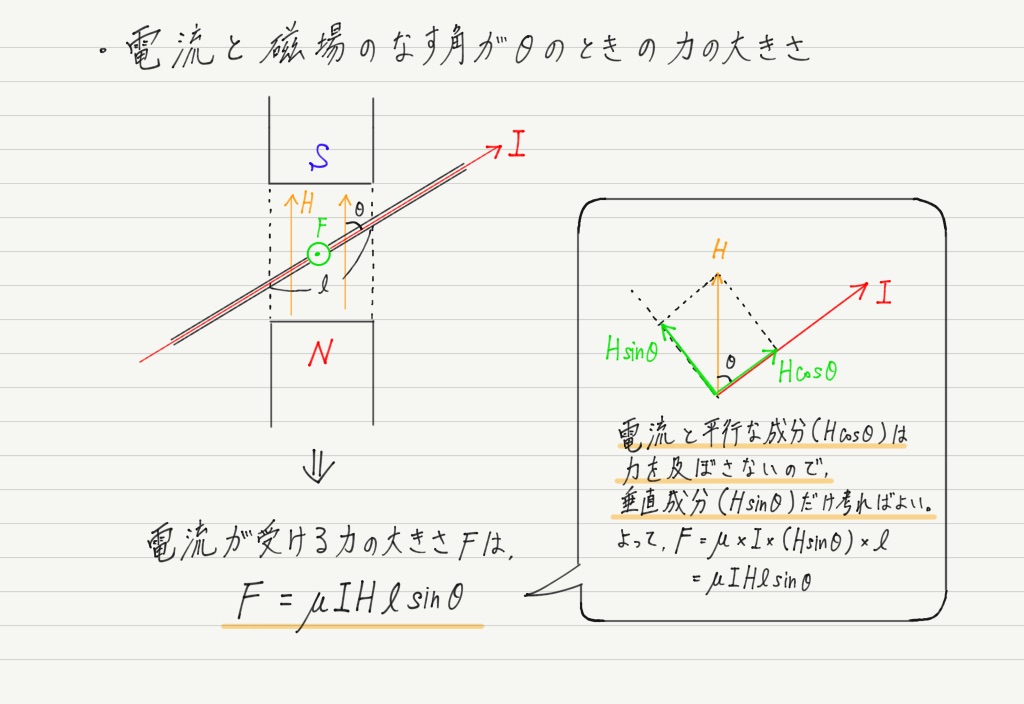
ここで登場した比例定数μは，透磁率と呼ばれています。 もし電流と磁場が斜めに横切っていたら，磁場を成分に分けて，電流と直角になる成分だけを考えてください。
今回のまとめノート
時間に余裕がある人は，ぜひ問題演習にもチャレンジしてみてください！ より一層理解が深まります。
次回予告
力の大きさの式に登場した比例定数μはただの比例定数ではなく，重要な意味をもっています。 次回はこのμにスポットを当てていきましょう！
