電気と磁気がとても似た性質をもっているので，「この2つは別物じゃなく，互いに関係しているんじゃないか…？」と考えるのは自然なことで，実際，密接に関連しあっています。
今回はそんな電気と磁気の間の基本的な関係について見ていきましょう。
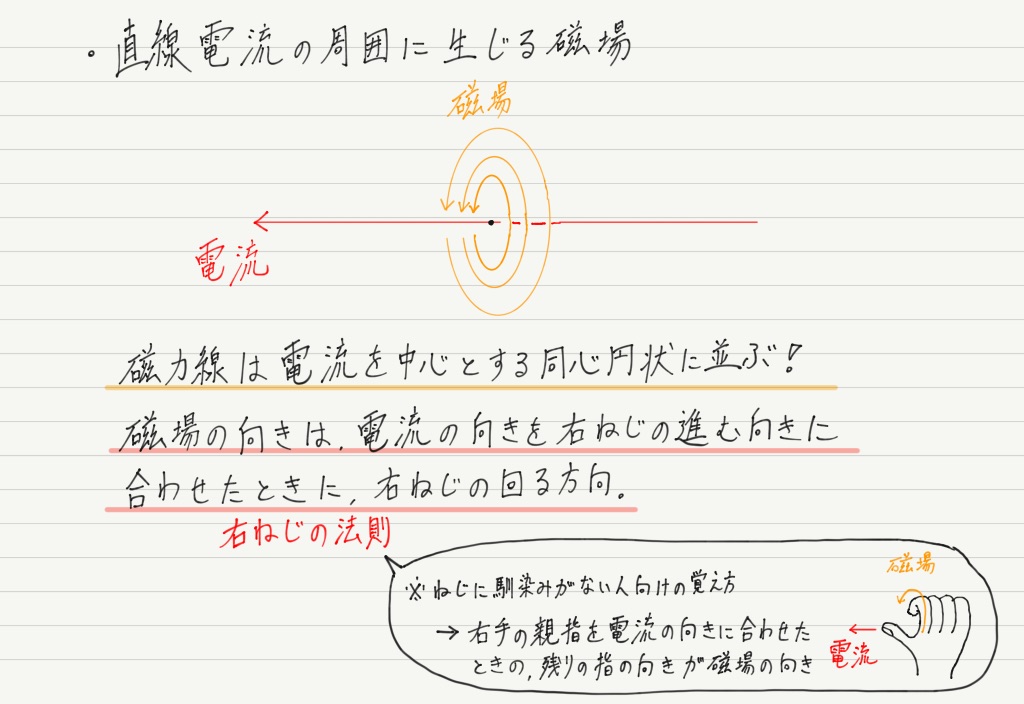
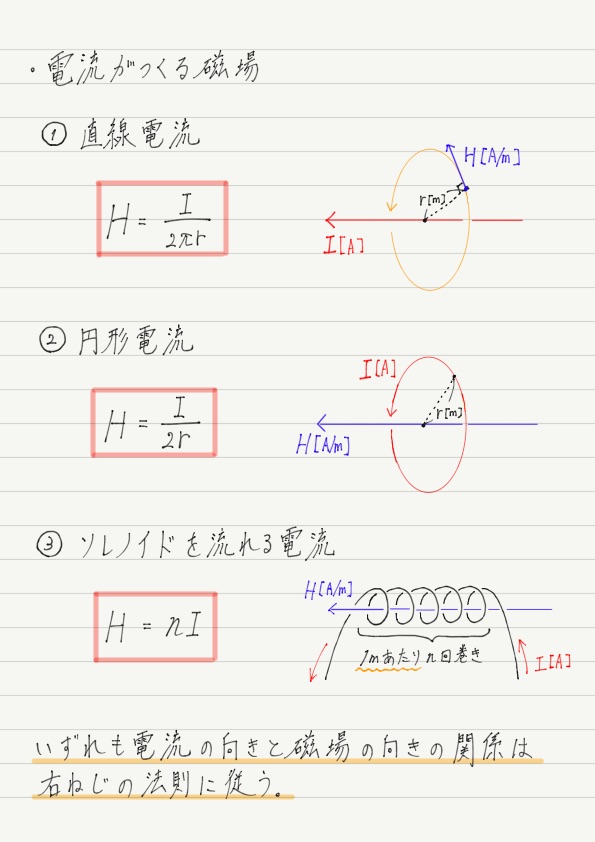
① 直線電流がつくる磁場
1820年，デンマークの科学者エルステッドは，直線状に張った導線に電流を流すと，そのまわりに磁場が発生することを発見しました。
この磁場の形と向きはとても重要なので，しっかり覚えてください。
エルステッド以前にも，電気と磁気には関係があるのではないか？と気づいていた人は数多くいたようですが，誰一人としてその関係を見つけられませんでした。
まぁ，上の図を見ればその理由もわかるような気がします。 まさか渦巻状に磁場ができるなんて想像できないじゃないですか！笑
人々が予想だにしなかった形状の磁場のおかげで，1820年にようやく発見された電流と磁場の関係。
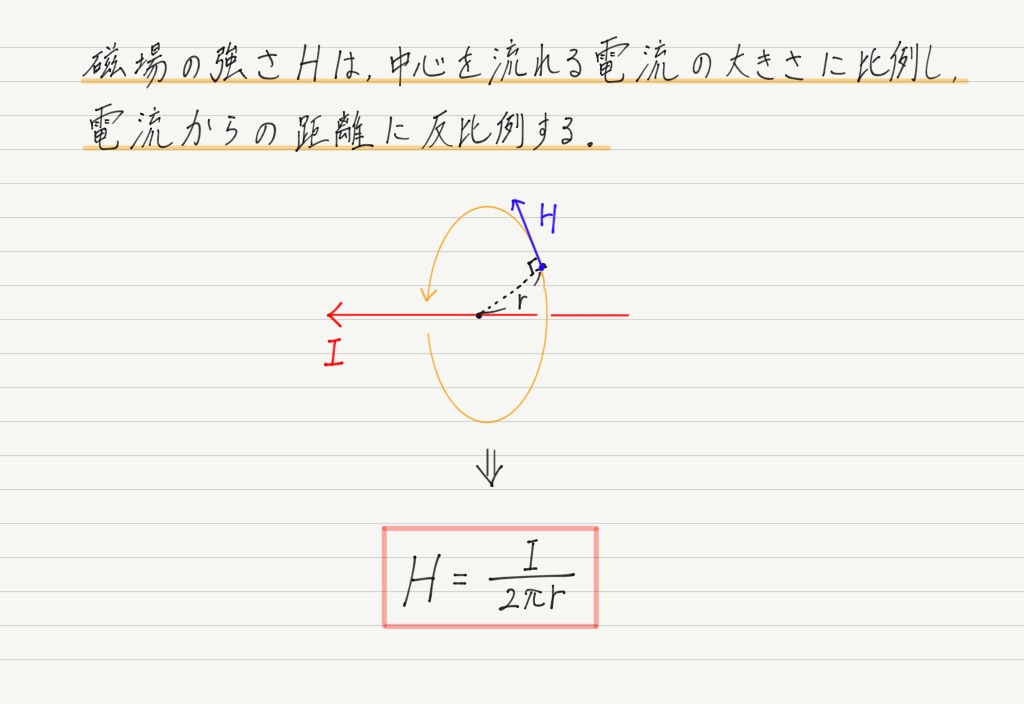
ところが，ここからの進展はものすごくスピーディー。 なんとエルステッドの発見から1週間後（！）には，流す電流の大きさと磁場の強さの関係がアンペールによって明らかにされています。
※ 補足：磁場の強さの単位について
上の式を見ると，磁場の強さ ＝ 電流［A］÷ 円周［m］なので，磁場の強さの単位はA/mだとわかります。 実は前回のまとめノートですでに紹介済み。
磁場の単位にはN/WbとA/mの2種類があります。 電場の単位もN/CとV/mの2つがあったので，やはり両者は似ていますね！
ただし，電場では2つとも使われるのに対し，磁場の場合は大抵A/mしか使いません 。 N/Wbは「1Wbの磁荷が受ける磁気力」という意味合いですが，磁荷がこの世に存在しない以上，あまり意味がないですからね(^_^;)
Wbという単位の存在感のなさよ…笑
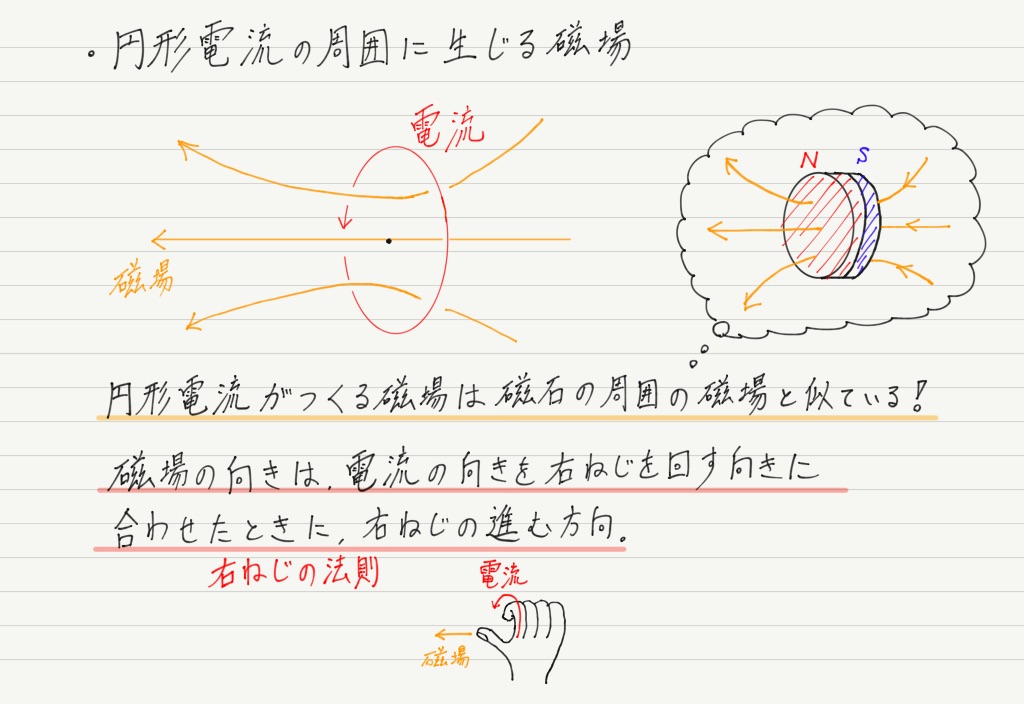
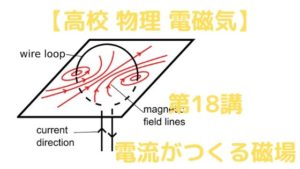
② 円形電流がつくる磁場
今度は電流を円形に流すことを考えましょう！
電流は回路に登場することが多いから，直線よりもぐるっと1周するほうが見慣れてるし，知っておいたほうがいいじゃない。 結果はこんな感じになります ↓
直線電流のときと同様に右ねじの法則に従っているので覚えやすいのではないでしょうか。
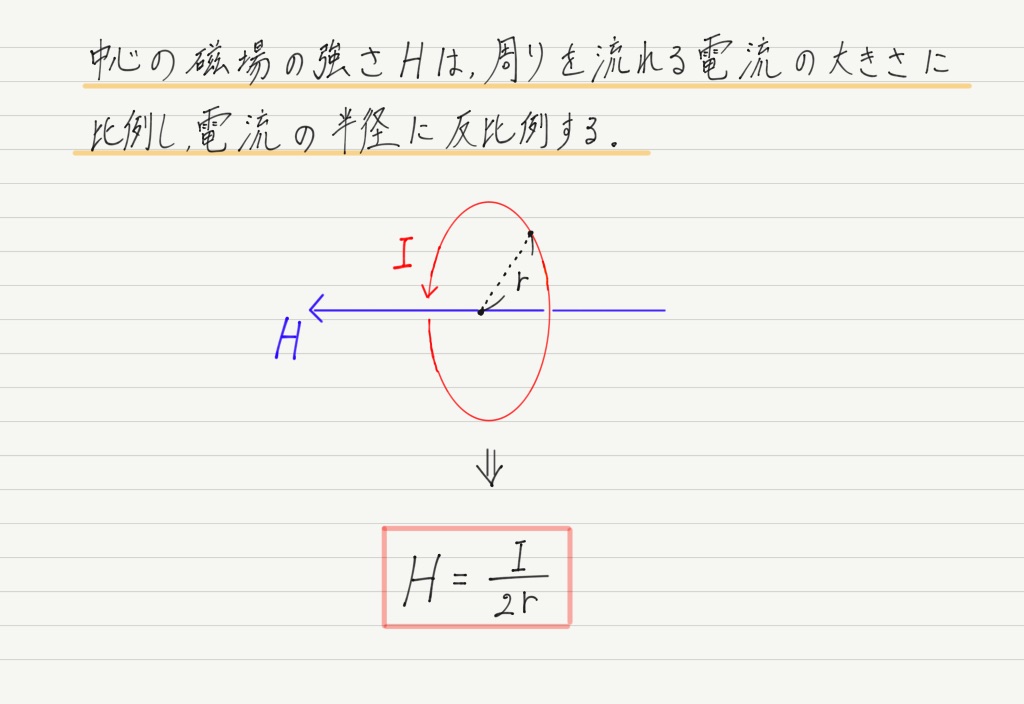
また，計算によって円形電流の中心にできる磁場の強さも求められます！
…おっと？ これはちょっと注意が必要です。 直線電流の場合と式は似ていますが，今回は分母に π が入っていません！！
どっちが 2πr でどっちが 2r だっけ？とならないように，しっかり区別して覚えてください。
③ ソレノイドを流れる電流がつくる磁場
最後に，ソレノイドがつくる磁場です！ その前に，「ソレノイドって何だ！説明しろ！」という声が聞こえてきたので（幻聴），まずはそちらの説明から。
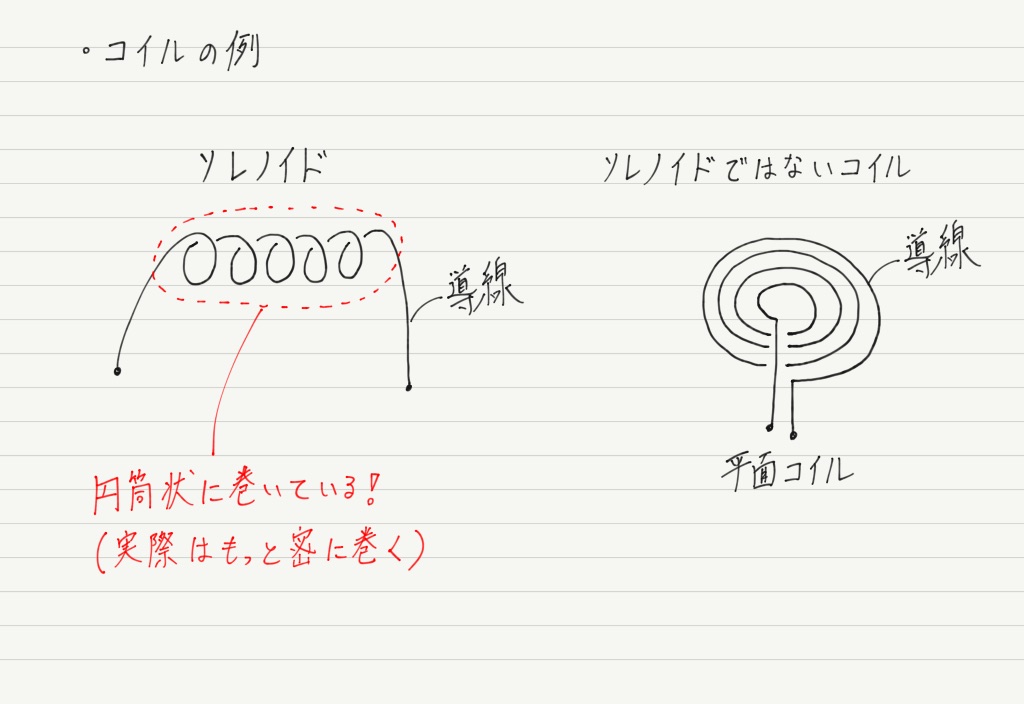
ソレノイドとは簡単にいうとコイルの一種です。 導線をぐるぐる巻いたものが俗に言うコイルですが，「巻く」と一口に言ってもいろいろな巻き方があります。
その中で特に，導線を円筒状に巻いたものをソレノイドと呼びます。
さて，ソレノイドに電流を流したときにできる磁場はどのような形でしょう？
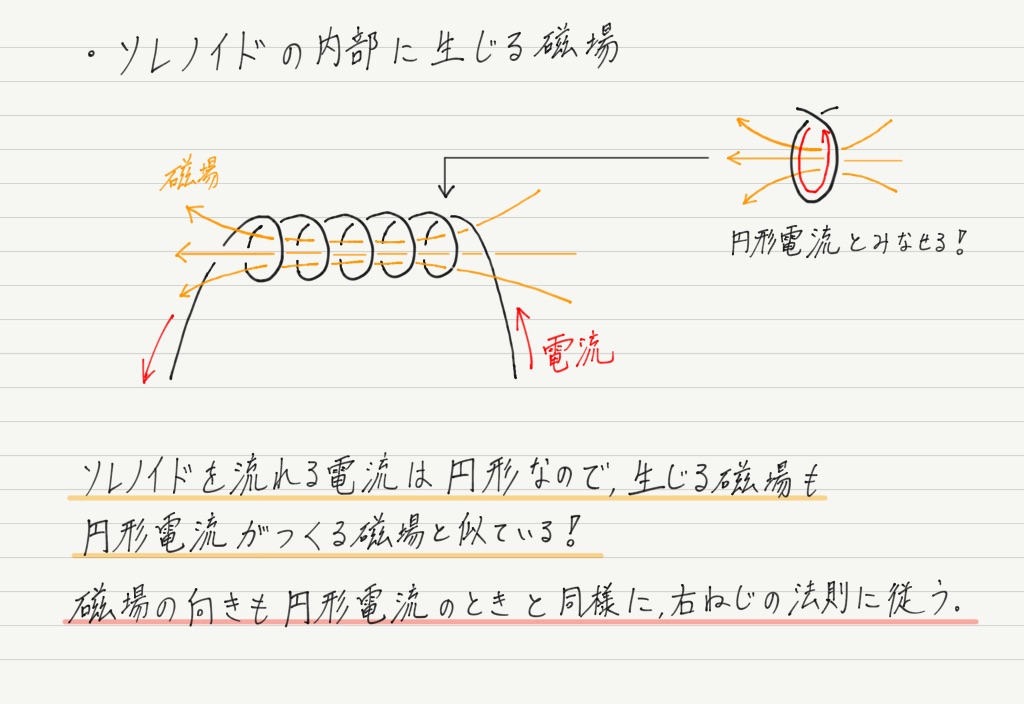
導線がぐるぐる巻きになっているので，電流もぐるぐる周りながら流れていきます。 ぐるぐる周りながら流れる電流。 それって円形電流ってことですよね！ つまり…
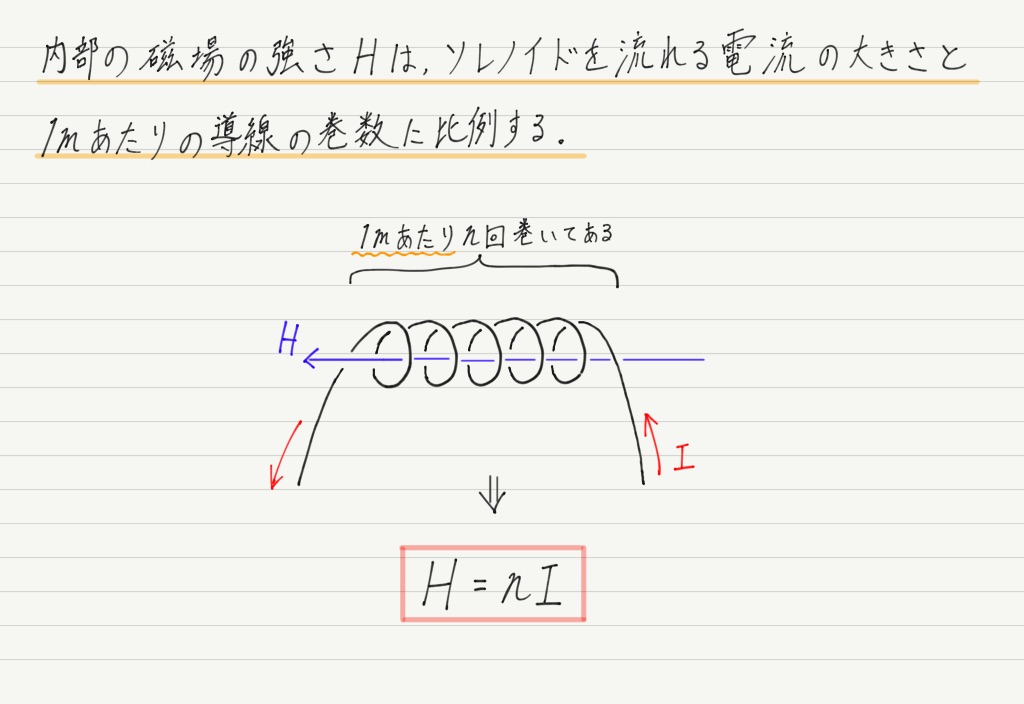
このような形の磁場が得られます。 ソレノイドの端では磁力線が広がっていますが，内部の磁場は一様です。 内部の磁場の強さを計算する公式もついでに伝授しましょう！
公式の中のnは単なる巻数ではなく，“1mあたりの” 巻数であることに注意してください！
以上，3パターンの電流がつくる磁場の形とその強さでした。
今回のまとめノート
時間に余裕がある人は，ぜひ問題演習にもチャレンジしてみてください！ より一層理解が深まります。
次回予告
磁場を生み出すだけが電流と磁場の関係ではありません！
