ひさしぶりに電気回路の問題を解いてみましょう。
物理基礎でやった回路は中学レベルと大して変わりませんでしたが,ここから本格的にレベルアップしていきます。
【復習】電気回路における原則
レベルアップするとは言っても,公式が変化したり,問題の解き方がガラッと変わる,というようなことはありません。
あくまでも簡単な問題の延長。
なので,まずは物理基礎のときに学習した「電気回路における原則」を思い出しておきましょう。
原則①:回路を流れる電流の量は増えたり減ったりしない。
原則②:電源で上がる電圧と,抵抗で下がる電圧は等しい。
原則③:抵抗の数だけオームの法則を用いる。
詳しい説明が欲しい!という方は,物理基礎の記事を読んでください。 これが理解できていないと,今回の内容も理解できないと思います。
オームの法則についても熟知しているものとして解説していきますよー
問題を解く上で大事なのは,オームの法則そのものよりも,原則①と②。
回路全体において,電流と電圧がどのような関係にあるのかを見極めないと問題は解けません。
「電気回路の問題=オームの法則」と思い込んでいる人は勉強不足ですよ!
キルヒホッフの法則とは
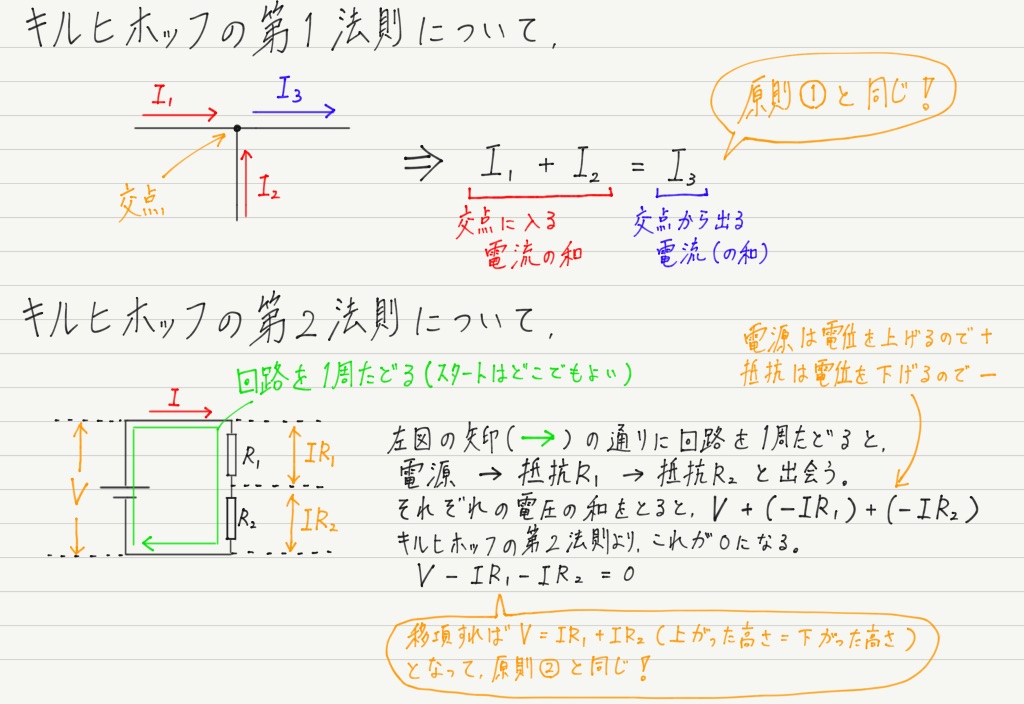
さて,今回のテーマである「キルヒホッフの法則」とは,まったく新しい法則ではなく,上で述べた原則を言い換えたものに過ぎません。 法則の内容を書いておきます。
ん?文章だけじゃよくわからないって?
大丈夫,そんな難しいことは言ってません。というかむしろ簡単。
第1法則は原則①そのまんまだし,第2法則は原則②をちょいと式変形しただけです。
具体例を挙げて説明しておくと,
こんな感じです。
ですが,ただの言い換えと思うなかれ。 こういうちょっとした工夫が問題を解きやすくしてくれるものなのです。
とはいえ,実際に問題を解いてみないと実感できないと思うので,例題を使って解説していきます!
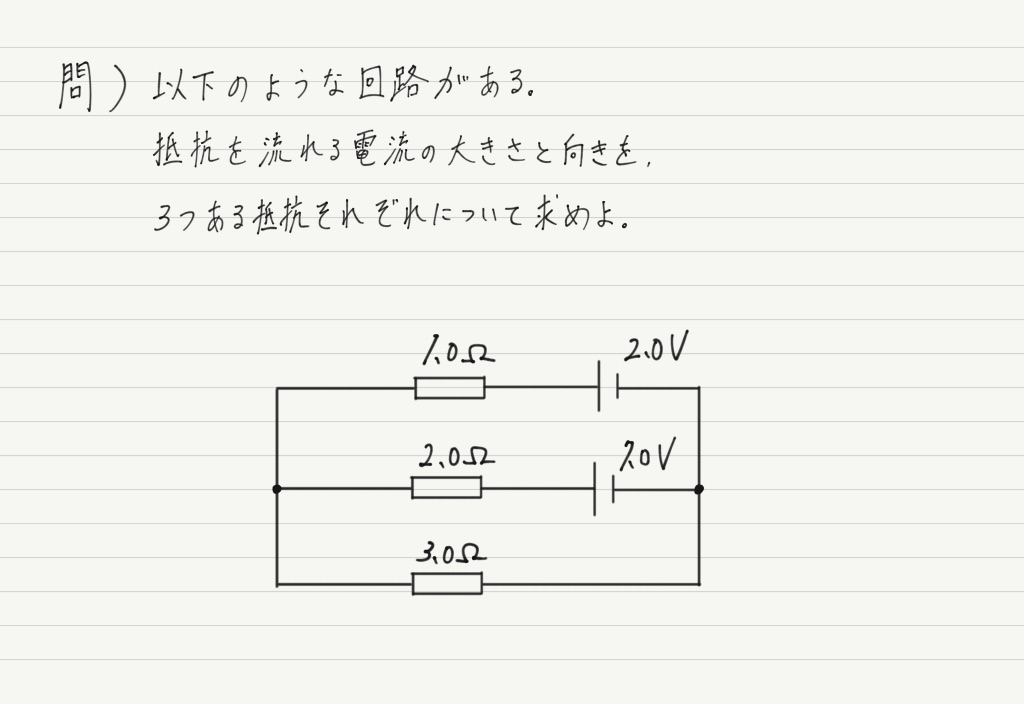
例題
物理基礎のときはイメージを大事にしたかったので,電源=階段,抵抗=すべり台といった表現を用いてきました。
実際,簡単な問題はそれで解けてしまいますが,今回の問題はどうでしょう?
階段とすべり台が入り混じっていて,イメージするのはちょっとキツそうです(抵抗はともかく,電源が複数散らばっているとイメージができなくなる事が多い)。
そんなときこそ,キルヒホッフの法則の出番。 具体的な使い方を伝授します!
イメージだけで回路全体を捉えるのは不可能でも,第2法則を使う際,「上がる」「下がる」という表現が出てくるので,階段やすべり台のイメージは部分的には役立つはずです。
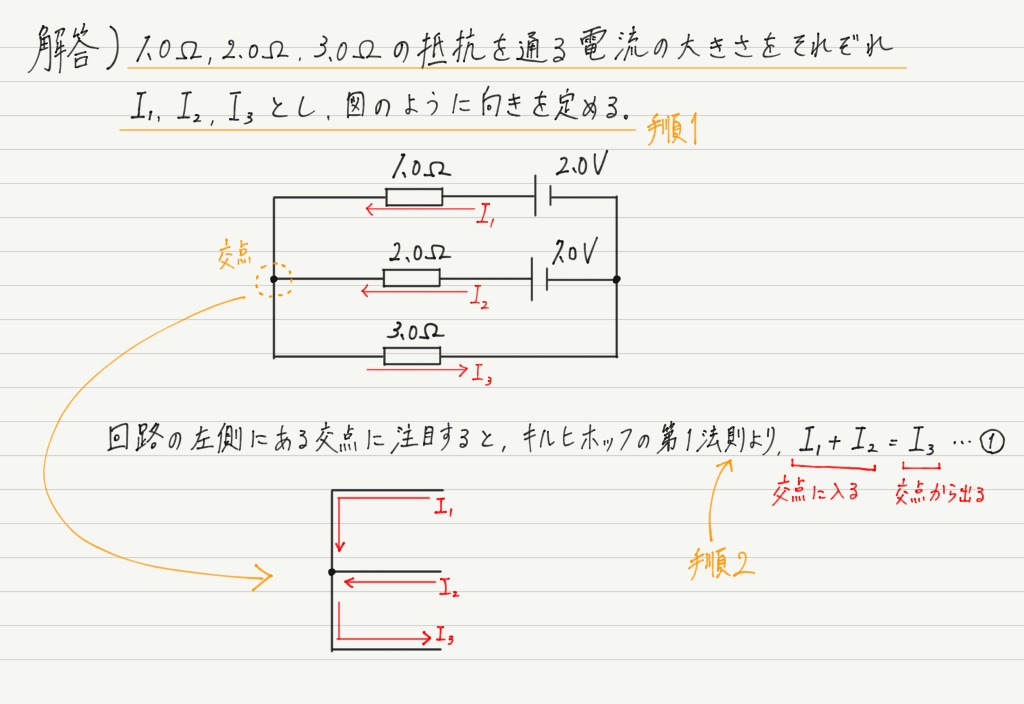
では,これを例題に適用してみます。
電流の向きはあくまでも「仮定」ですが,電源の向きから考えるとこれが妥当な気がします。
解答の続きをどうぞ。
これがキルヒホッフの法則を用いた回路の問題の解き方です。
注目してほしいのは,1.0Ωの抵抗を通る電流を求めたら負になってしまったこと。
回路図を見ただけだと左向きで正しいような気がしますが,答えが負ということは実際は右向き。
一見単純そうに見えるこの問題でさえ,こういうことが起こります。
全体のイメージをつくる場合,このような電流の向きの間違いは致命的ですが,イメージせずに機械的に計算できるキルヒホッフの法則ならば安心。
仮に向きを間違えていても今みたいに符号が教えてくれます。
最初に書いたとおり,キルヒホッフの法則は以前やった「電気回路における原則」の言い換えに過ぎません。
ですが,言い換えただけでずいぶん便利になっていると思いませんか?
ぜひ使いこなせるようになってください!
練習問題
上と同じ例題をちがう方法で解いてみましょう。
電流の仮定と,1つ目の経路(F→A→C→D→F)はさっきと同じままで,2つ目の経路をF→A→B→E→Fとして,計算してみてください。
解答はこの下にあります。
できましたか? 答え合わせしてみましょう!
当然ですが,同じ答えが得られます。
同じ答えが出るなら計算はなるべく簡単になる方がよいので,問題集で類題をいろいろ解いてみて,どの経路を考えれば一番簡単に解けそうかを見極める目を養ってください!
今回のまとめノート
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。
次回予告
回路の話はまだ続きます。
前回せっかくコンデンサーをやったので,抵抗だけでなくコンデンサーも回路につないでみましょう!