充電されたコンデンサーに豆電球をつなぐと,コンデンサーに蓄えられた電荷が移動し,豆電球が一瞬光ります。
何もないところからエネルギーは出てこないので,「コンデンサーに蓄えられていたエネルギーが豆電球の光エネルギーに変換された」と考えるのが自然です。
コンデンサーは電荷を蓄える装置ですが,今回はエネルギーの観点から見直してみましょう!
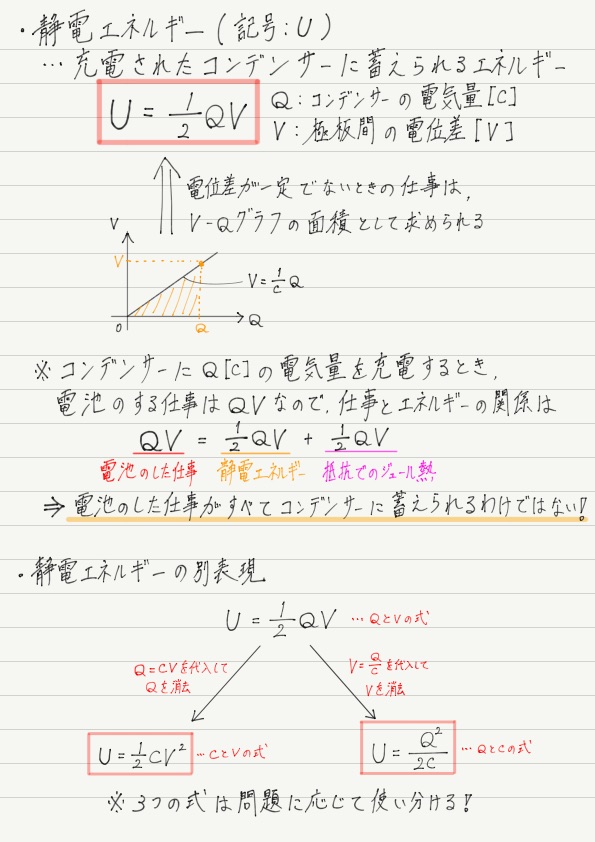
静電エネルギーの式
エネルギーとは仕事をする能力のことだったので,豆電球をつないだときにコンデンサーがどれだけ仕事をするか求めてみましょう。
まずは復習。
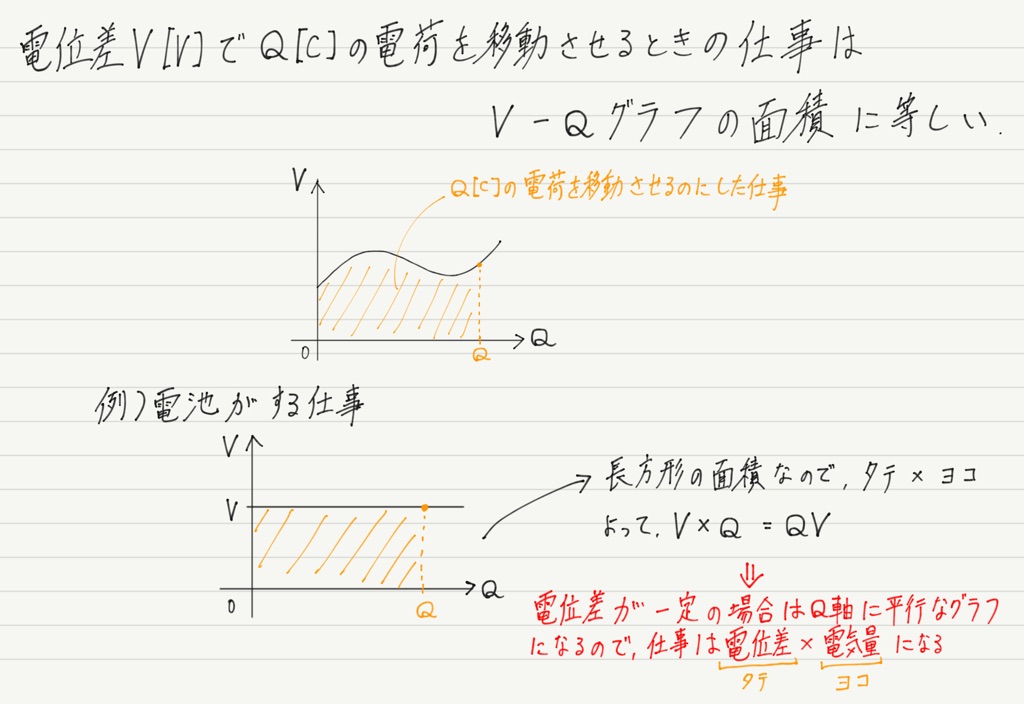
電位差Vの電池が電気量Qの電荷を移動させるときの仕事WはW=QVで求められました。
ピンとこない人はこちら↓を読み直してください。
さて,充電されたコンデンサーを豆電球につなぐと,蓄えられた電荷が極板間の電位差によって移動するので電池と同じ役割を果たします。
電池と同じ役割ということは,コンデンサーに蓄えられた電気量をQ,極板間の電位差をVとすると,コンデンサーのする仕事もQVなのでしょうか?
結論から言うと,コンデンサーのする仕事はQVではありません。
なぜかというと,電池とちがって極板間の電位差が一定ではない(電荷が流れ出るにつれて電位差が小さくなる)からです!
では,どうするか? 弾性力による位置エネルギーを求めたときを思い出してください。
弾性力Fが一定ではないので,ばねのする仕事Wは単純にW=Fxではなく,F-xグラフの面積を利用して求めましたよね!
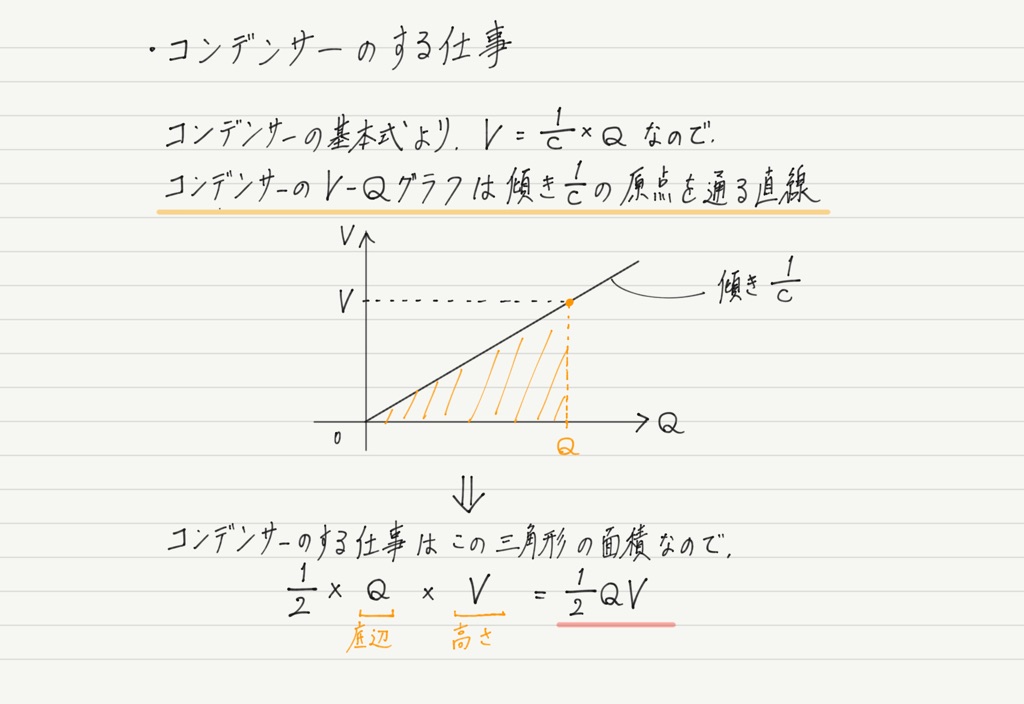
そこで今回も,V-Qグラフの面積から仕事を求めることにします!
「コンデンサーがする仕事の量=コンデンサーがもともと蓄えていたエネルギー」なので,これでコンデンサーに蓄えられるエネルギー(静電エネルギーという)が求められたことになります!!
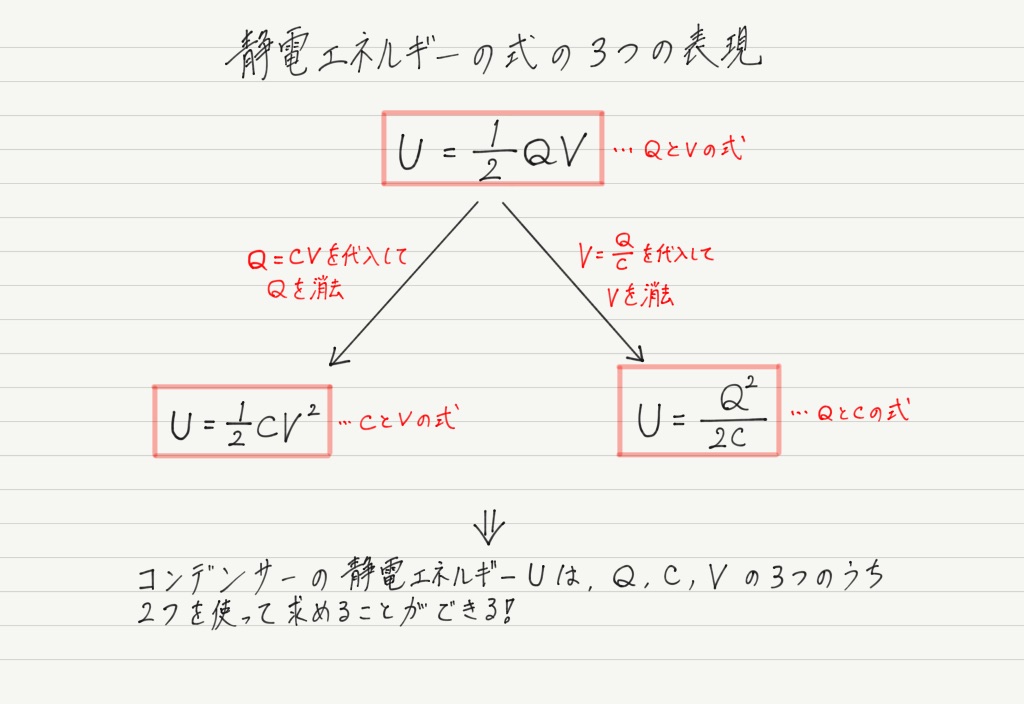
ここで,得られた静電エネルギーの式をコンデンサーの基本式を使って式変形してみましょう。
この3種類の式は問題によって使い分けることになるので,自分で導けるようにしておくこと!
例題 〜式の使い分け〜
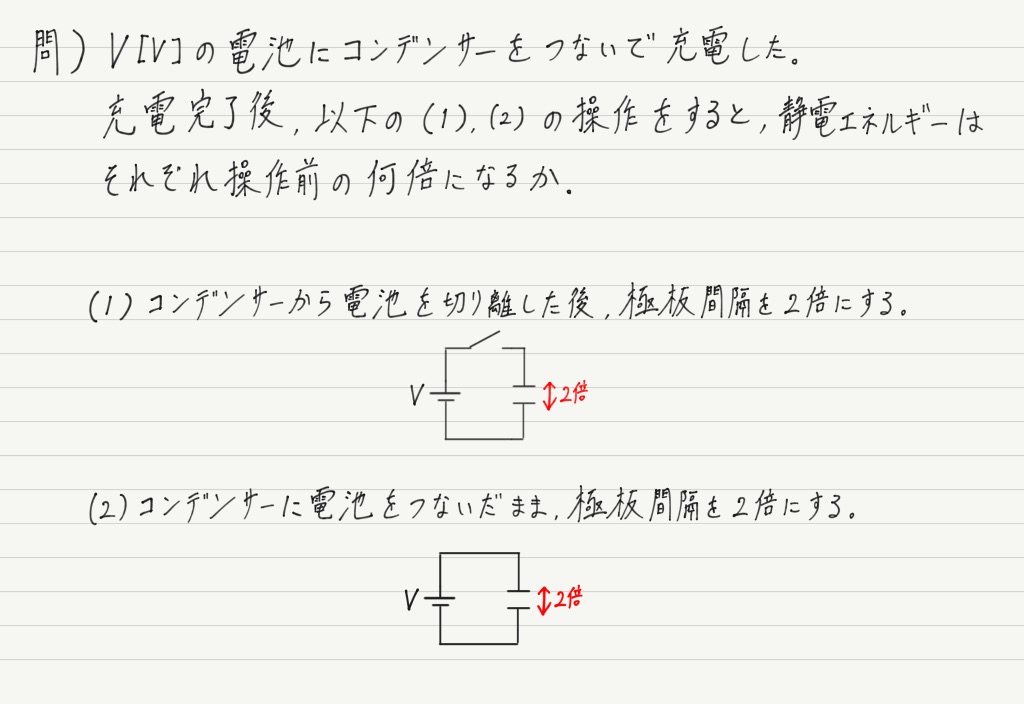
では,静電エネルギーに関する例題をやってみましょう。
このように,極板間隔をいじる問題はコンデンサーでは頻出です。
電池をつないだままのときと,電池を切り離したときで何が変わるのか(あるいは何が変わらないのか)を,よく考えてください。
解答はこの下にありますが,まずは自力でやってみてください。
では解答です。
極板間隔を変えたのだから,電気容量が変化するのは当然。
次に電池を切り離すか,つないだままかで “変化しない部分” に注目します。
「変わったものではなく,変わらなかったものに注目」するのは物理の鉄則!
静電エネルギーの式は3種類ありますが,変化がわかりやすいもの(ここではC)と,変化しなかったもの((1)ではQ,(2)ではV)を含む式を選んで用いることで上記の解答が得られます。
感覚が掴めたら,あとは問題集で類題を解いて理解を深めておきましょうね!
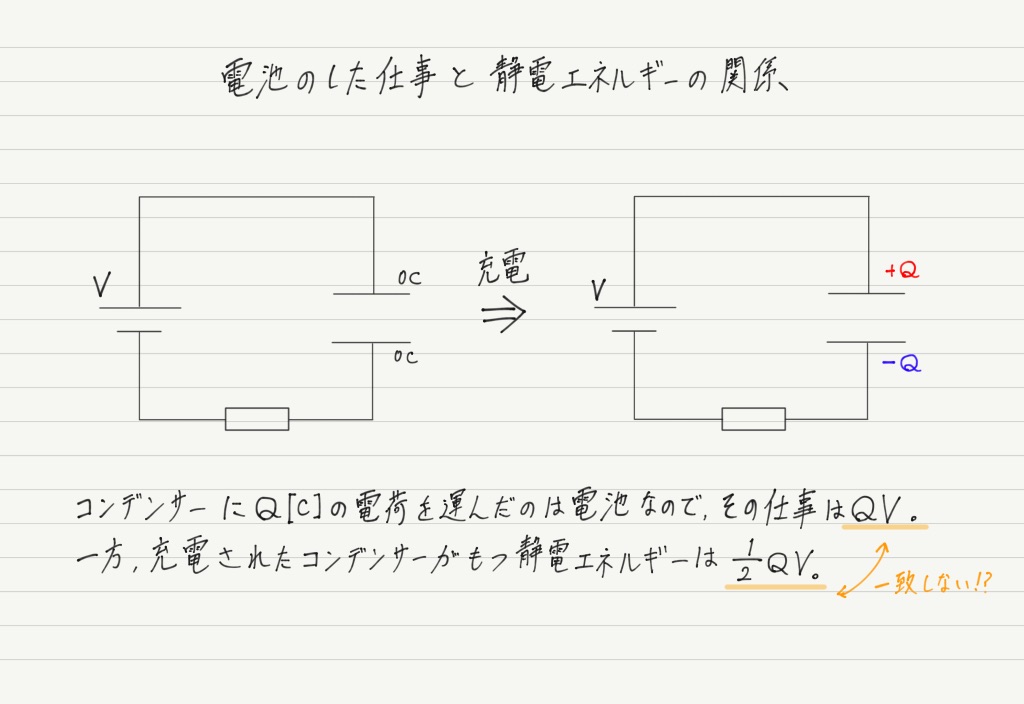
電池のする仕事と静電エネルギー
最後にコンデンサーの充電について考えてみましょう。
力学であれば,静止した物体に30Jの仕事をすると,その物体は30Jの運動エネルギーをもちます。
された仕事をエネルギーとして蓄えるのです。
ところが今回の場合,コンデンサーに蓄えられたエネルギーは電池がした仕事の半分しかありません!
残りの半分はどこへ??
実は充電の過程において,電池がした仕事の半分は導線がもつ抵抗で発生するジュール熱として失われるのです!
電池のした仕事が,すべて静電エネルギーになるわけではないので要注意。
それにしても半分も熱になっちゃうなんて,ちょっともったいない気がしますね。
今回のまとめノート
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。
次回予告
そろそろ回路の問題が恋しくなってきませんか?