前回紹介したコンデンサーについて,さらに理解を深めていきましょう!
今回の記事を読む前に,ガウスの法則や電場と電位の関係についての記事をあらかじめ読んでおくことをおすすめします。
極板間の電場を調べる
コンデンサーとは面積の等しい2枚の極板を平行に配置したものでした。
電池をつないで充電するとそれぞれが正と負に帯電するわけですが,このときの電場の様子が今回の大きなテーマです。
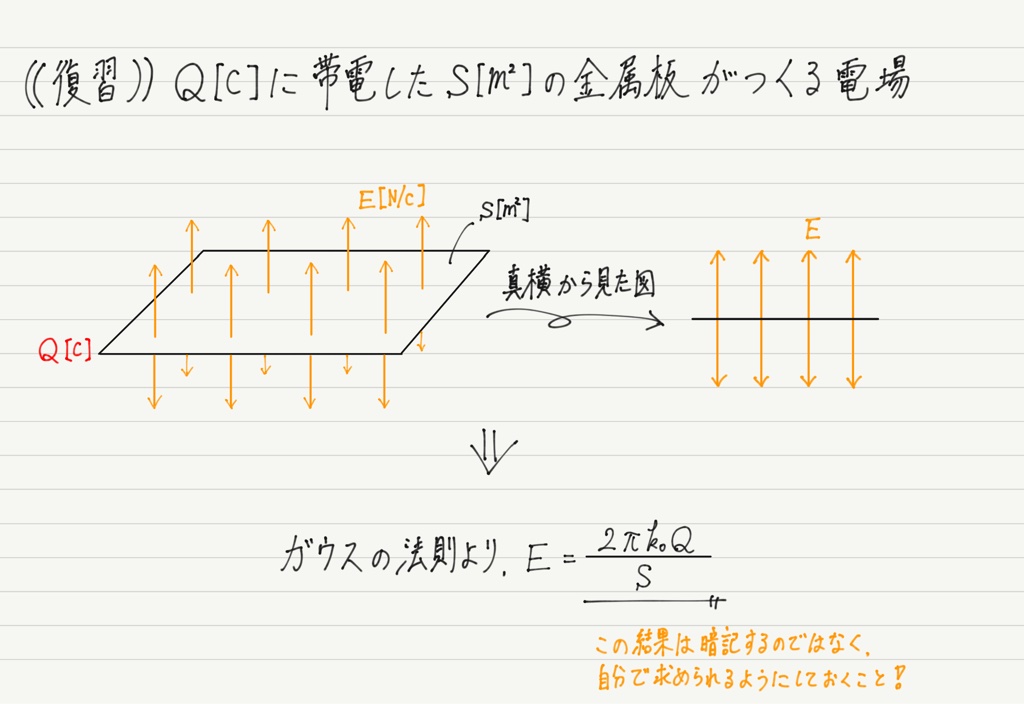
帯電した金属板(平面電荷)がつくる電場については,以前ガウスの法則の記事の例題で求めました。
結果だけ載せておきますね!
この結果を利用して,コンデンサーの電場を求めてみましょう。
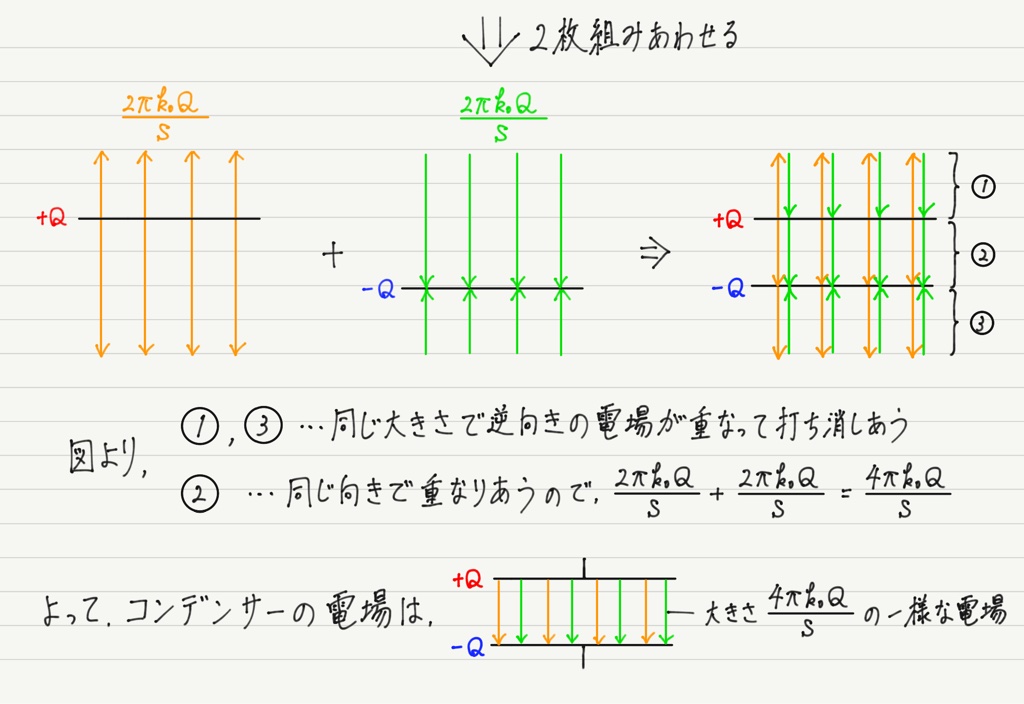
別に難しい計算はいりません。 極板を2枚用意して,それぞれの電場を重ねあわせるだけ!!
このように,極板の外部に電場はなく,極板間には一様な電場が生じていることがわかります。
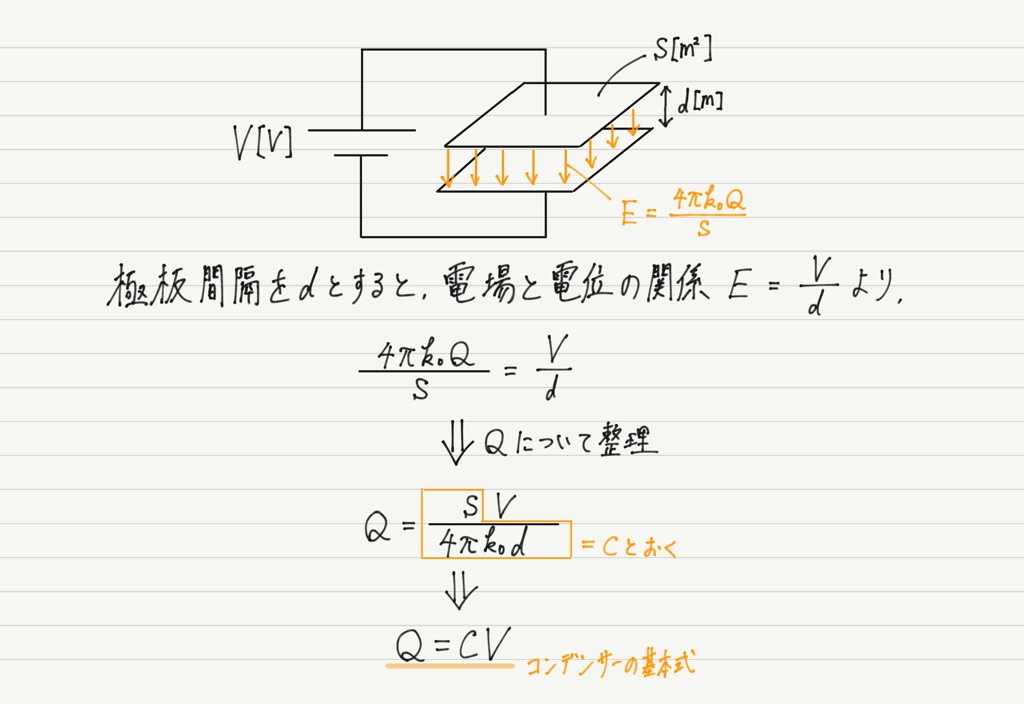
一様な電場ということは,この電場の強さと極板両端の電位差との関係式を立てることが可能。
実際にやってみましょう。
なんと! 前回やったコンデンサーの基本式が得られました!!
QとVが比例する理由について前回触れませんでしたが,電場について調べることで,このように自然に導かれる結論なのです。
ついでに電気容量Cの正体も明らかになったので詳しく調べてみましょう。
コンデンサーの形状と電気容量
上で得られた式をもう一度よく見てみましょう。
電気容量とは,コンデンサーにどれぐらい電気量が蓄えられるかの指標です。
わかったことをまとめると,
・電気容量は極板の面積に比例する
→極板は広ければ広いほどたくさん電気を蓄えられる。
・電気容量は極板間の距離に反比例する
→極板間隔は狭ければ狭いほどたくさん電気を蓄えられる。
このうち面積については直感的に当たり前に感じられると思います。 距離についてはどうでしょう?
お互いの極板にある電荷どうしは静電気力で結びついているので,距離が短いほうが結びつきが強くなり,たくさん電荷を保持しておけます。
誘電体と誘電率
極板の面積・間隔とともに大事なのが比例定数です。
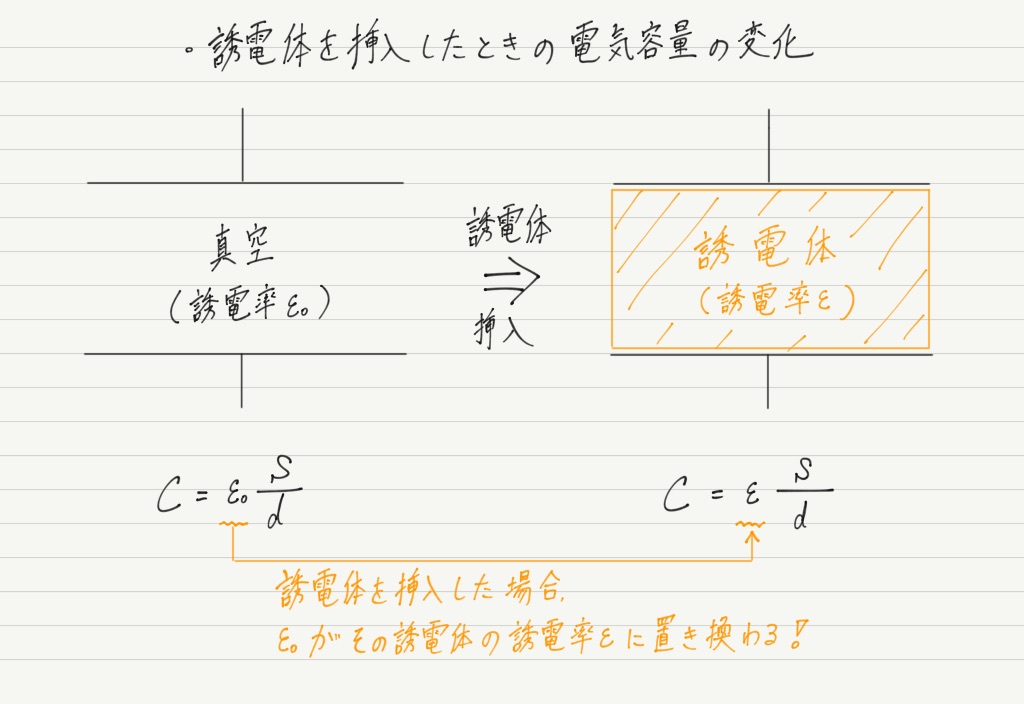
極板間が真空の場合は上の式で見たように,比例定数として真空の誘電率が用いられます。
しかし現実に使われているコンデンサーは,極板間に何か他の物質(誘電体)が挿入されていることがほとんどです。
(※ 誘電体とは不導体の別名。コンデンサー関連では誘電体という名称が好んで使われる。)
結論を先に言ってしまうと,コンデンサーに誘電体を挿入した場合,誘電率が変化して電気容量は増加します。
ここで1つだけ注意しておきたいのは物質の誘電率の表し方。
コンデンサーの問題では,「この誘電体の誘電率は◯◯です」のように,値が直接与えられる場合もありますが,この他に比誘電率が与えられる場合もよくあります。
比誘電率とは,「真空の誘電率の何倍か」を表す量です。
(※ どんな誘電体でも挿入すれば必ず電気容量は増えるので,比誘電率は必ず1より大きい。)
物質の誘電率と比誘電率,どちらもよく使うので,混乱しないようにちがいをちゃんと理解しておきましょうね!
誘電体を入れると電気容量が増える理由
なぜ誘電体を入れただけで電気容量が変化するのか。
しかも減るのではなく増えるのはなぜか。 最後にその理由を考えてみましょう。
まず普通にコンデンサーを充電します。
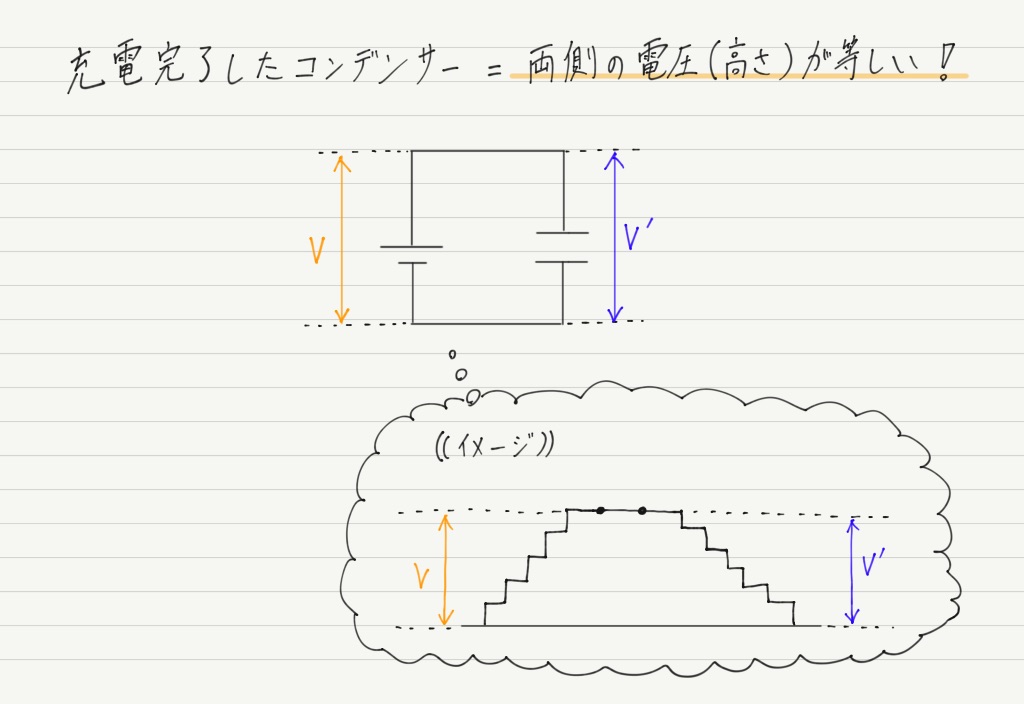
充電完了したとき,極板間の電位差と電池の電圧は等しいということを思い出してください。
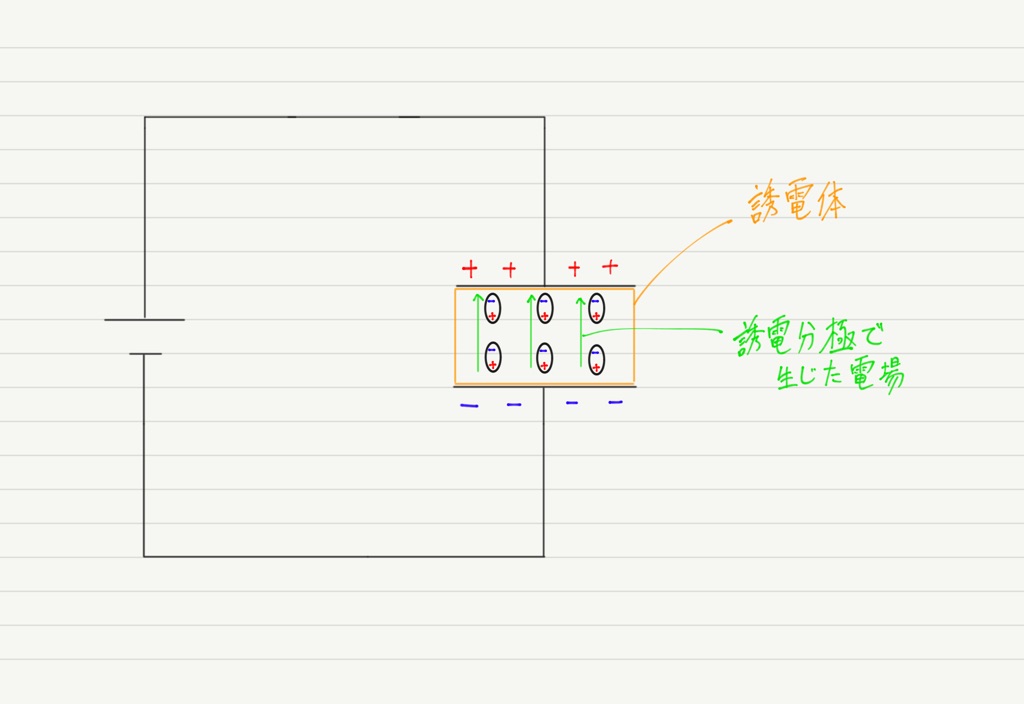
充電完了したコンデンサーに誘電体を入れると,誘電体は誘電分極し,内部に電場が生じます(向きに注意!)。
誘電分極の結果何が起こるでしょうか。
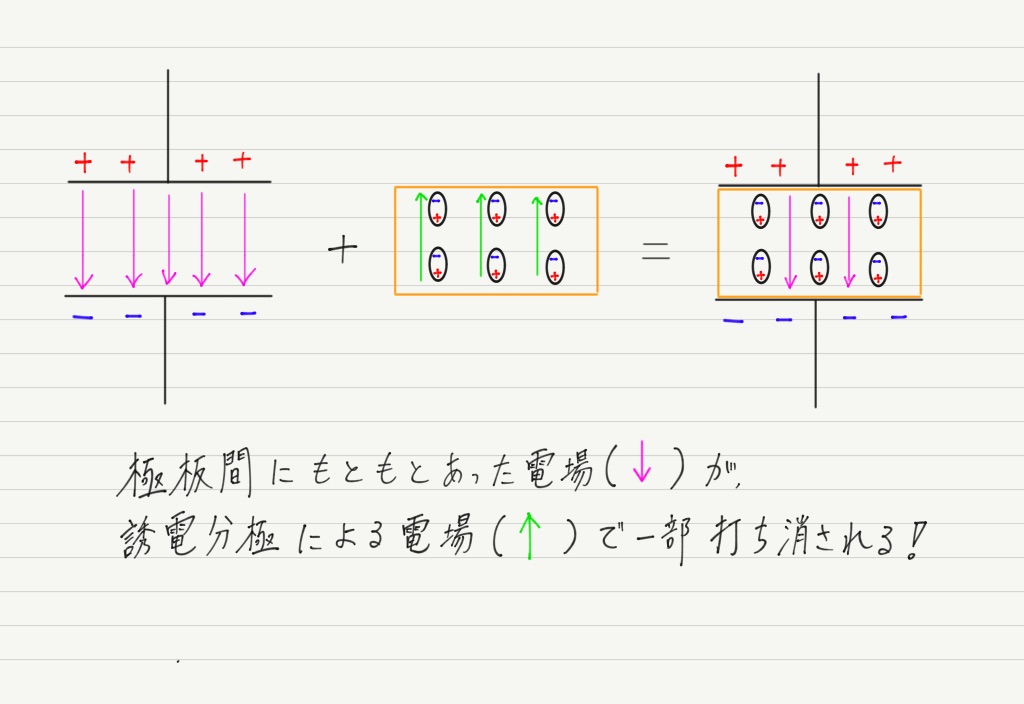
それは極板間の電場の打ち消しです!!
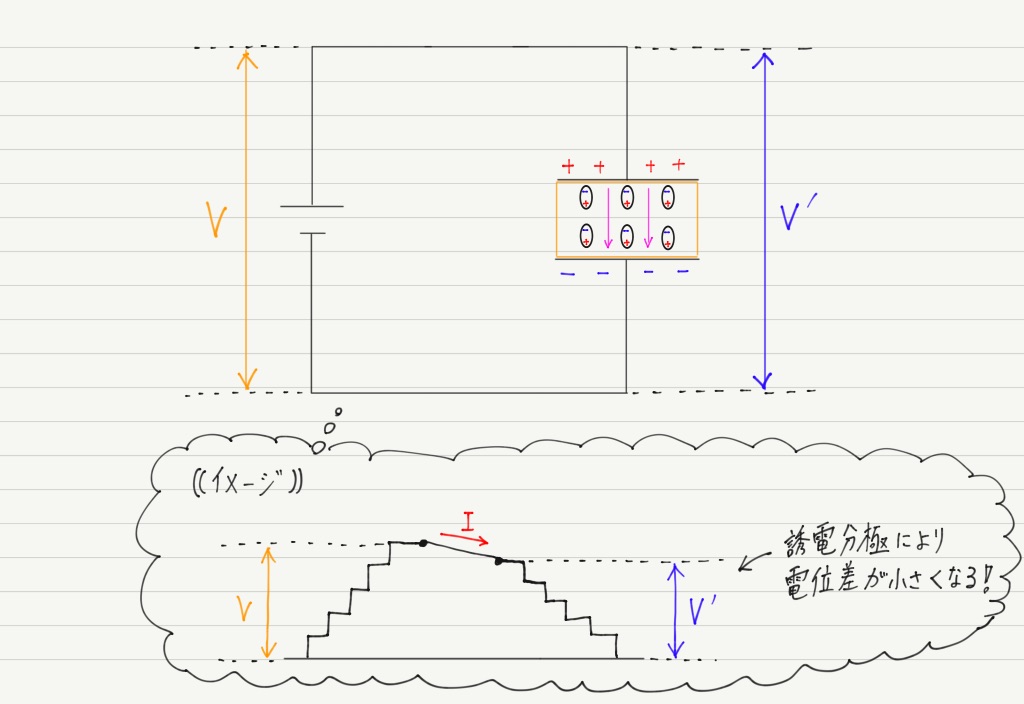
極板間の電場が弱まるということは,極板間の電位差も小さくなるということですね!
極板間の電位差が小さくなると,再び電流が流れはじめ,再び同じ高さになるまでコンデンサーに電気量が追加されます。
ちょっと長くなったのでまとめておきましょう。
① 誘電体を挿入すると誘電分極が起こる。
② 誘電分極によって生じる逆向きの電場によって極板間の電位差が減少する。
③ 減少した電位差を埋めようとして余計に電気量が補充される。
④ その結果,何もない場合に比べて多くの電気量がコンデンサーに蓄えられる。
これが,誘電体挿入による電気容量増加の一連のメカニズムです。
今回のまとめノート
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。
次回予告
次回はコンデンサーに蓄えられた電気をエネルギーの観点から見直してみたいと思います!