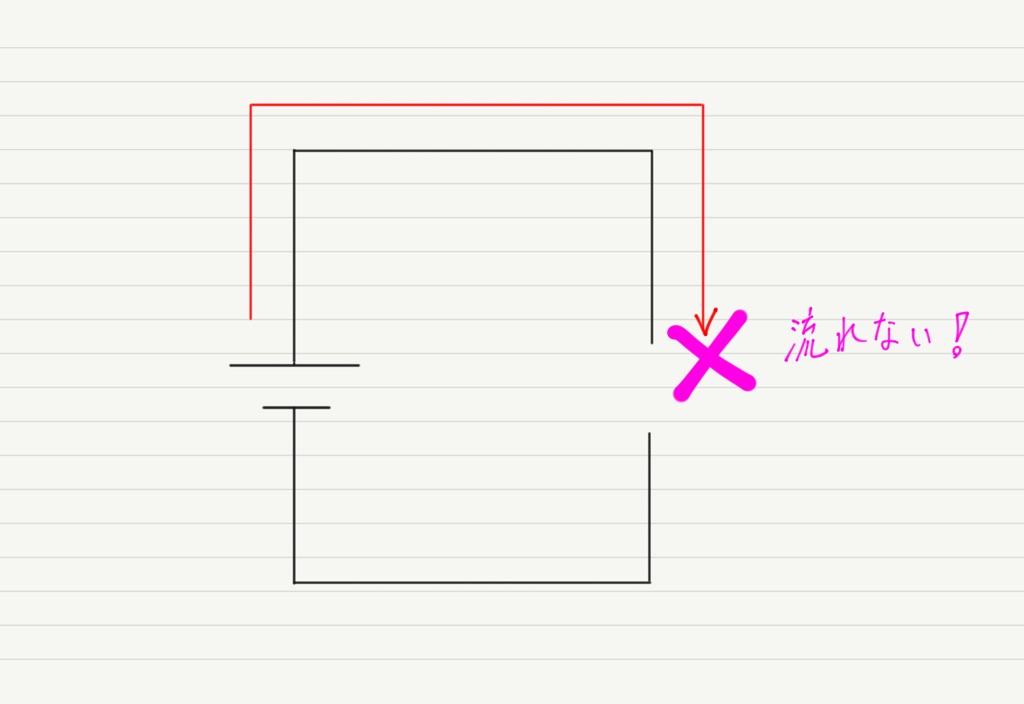
断線した回路に電流は流れません。
ところが,断線した箇所の上と下にそれぞれ金属板をくっつけると…
なんと! 一瞬だけ電流が流れるのです!!
金属板どうしは離れているので,最初の断線のときと状況は大して変わらないように思えますが,なぜ金属板を挟むと電流が流れるのでしょうか?
コンデンサーの原理
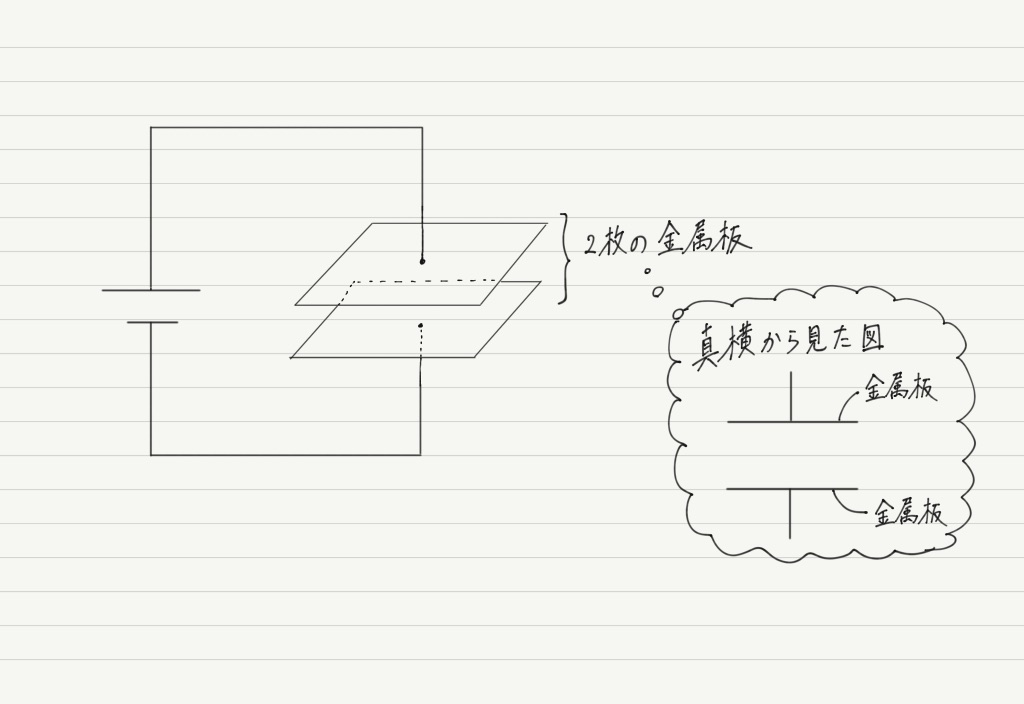
上の図のように,同じ面積の2枚の金属板(極板と呼ぶ)を向かい合わせたものを「コンデンサー」といいます。
(※ ちなみにコンデンサーは和製英語。英語ではキャパシターという。)
中学校の理科でも物理基礎の電気分野でも,ほとんど電池と抵抗だけの回路しか見てこなかったので,念願の新しい部品です!
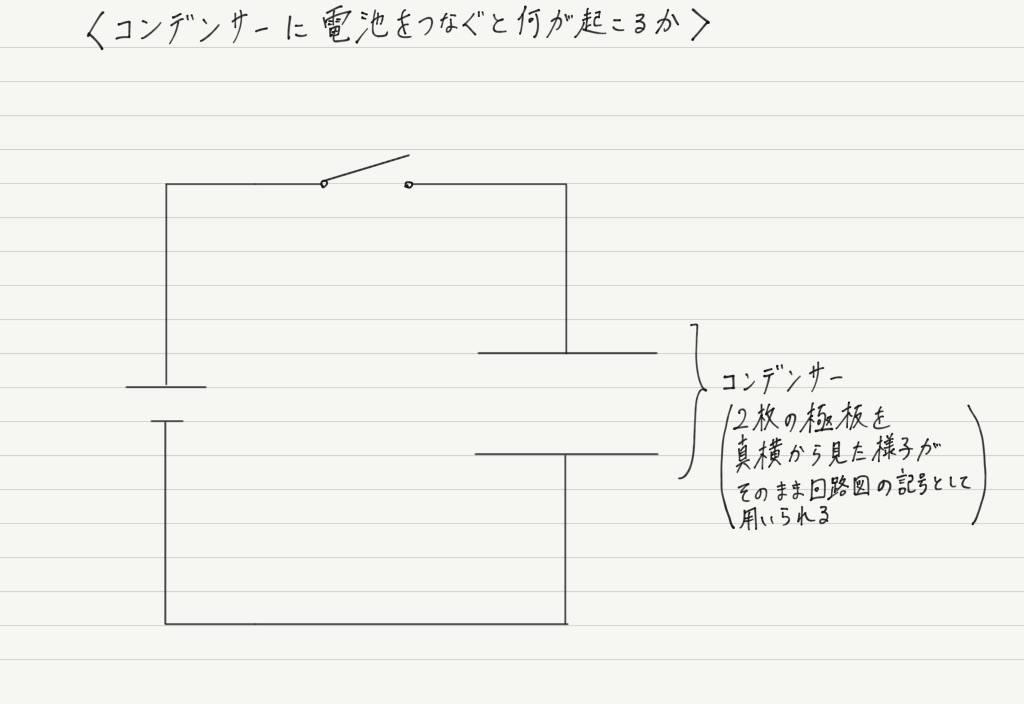
とはいえ,金属板をただ2枚挟んだだけで一体何ができるというのでしょうか? 図を使いながら説明していきます。
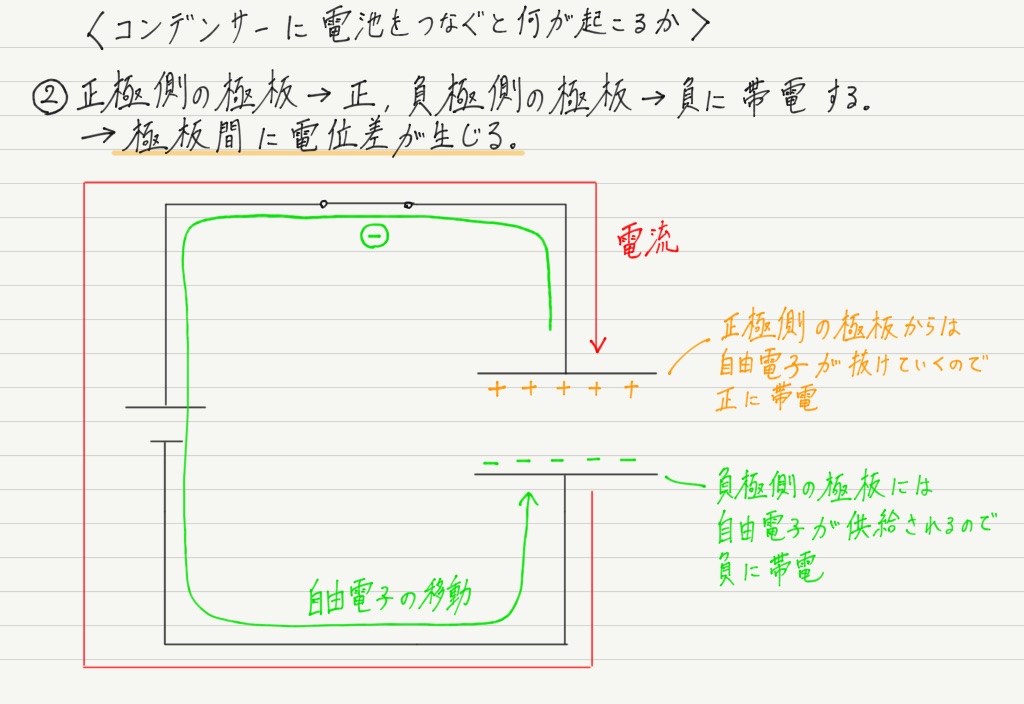
ではスイッチON。
コンデンサーの2枚の極板の間はつながっていませんが,電池はそんなこと知ったこっちゃありません。
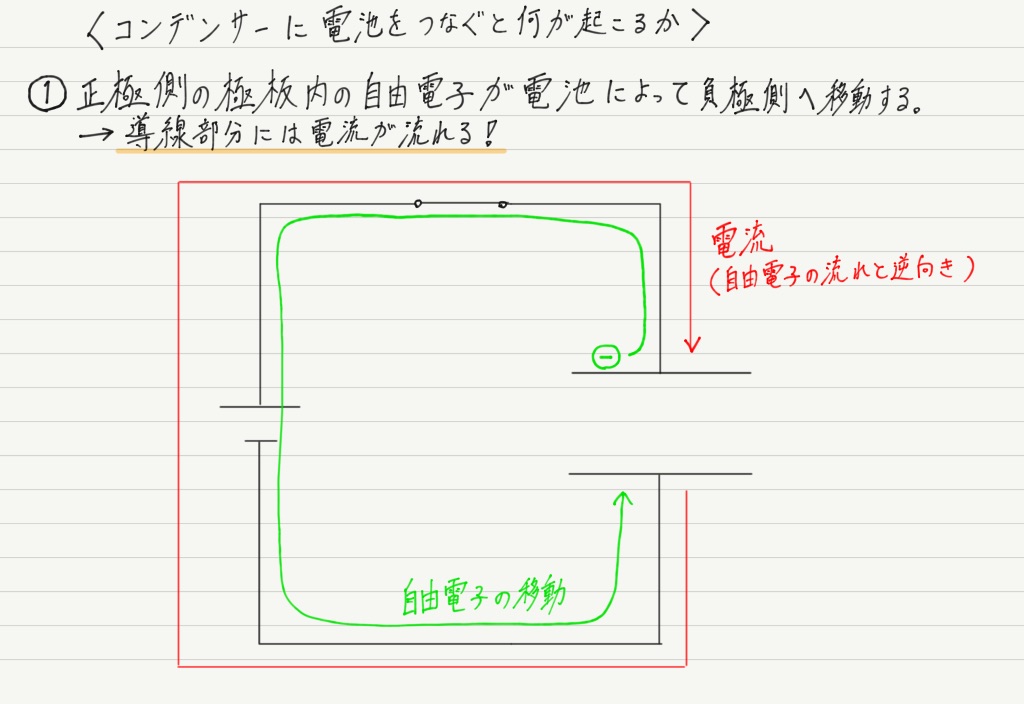
電池はいつもどおり自由電子を運ぼうとします。
極板は金属なので自由電子が豊富に存在しており,それが電池によって運ばれることになります。
この自由電子の移動によって,極板は徐々に帯電していきます。
また,帯電した極板間には電場が生じる(正電荷から負電荷に向かって電気力線が生じる)ので,同時に電位差も生まれます。 電場あるところに電位あり。忘れている人は復習しておきましょう。
自由電子の移動が進むにつれて極板にたまる電気量は増えます。
それに伴って極板間の電場も強まり,電位差も大きくなります。
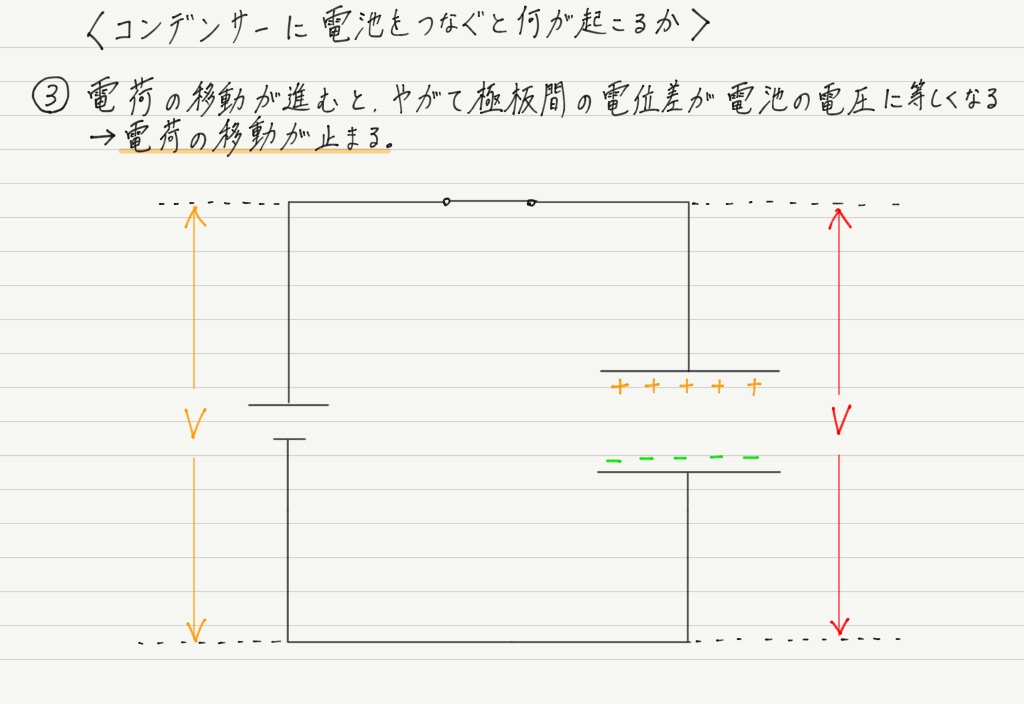
極板間の電位差が電池の電圧と等しくなったら,そこで自由電子の移動がストップ。 それ以降電流は流れなくなります。
(スイッチONしてから③の状態になるまでの時間は,実際にはごくわずか。)
「両方の電圧が等しくなったら電流が流れない」と聞いて,当たり前だと思えた人はOK。
え?なんで?と思った人のためにイメージも用意しておきます。
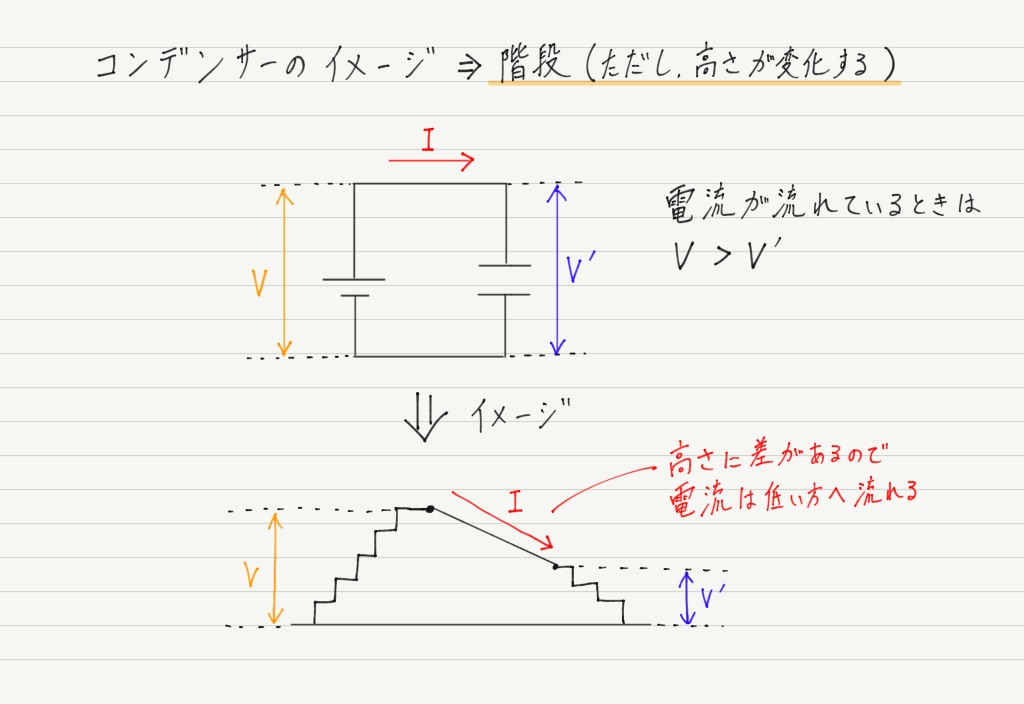
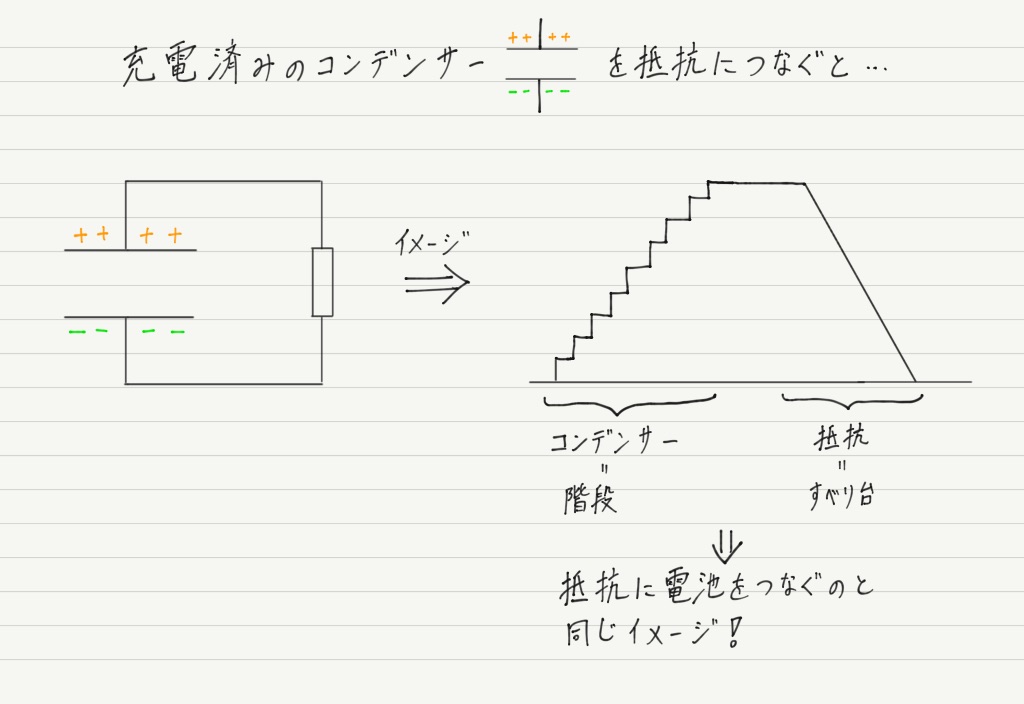
物理基礎では抵抗を“すべり台”のイメージでとらえましたが,コンデンサーは電池と同じく“階段”のイメージです。
ただし,コンデンサーの“階段”は,“徐々に高くなる階段(=だんだん電位差が増える)” なので注意が必要です。
電池を接続して最初のうちは電池のほうが高いので,低い方へ電流が流れ込みます。
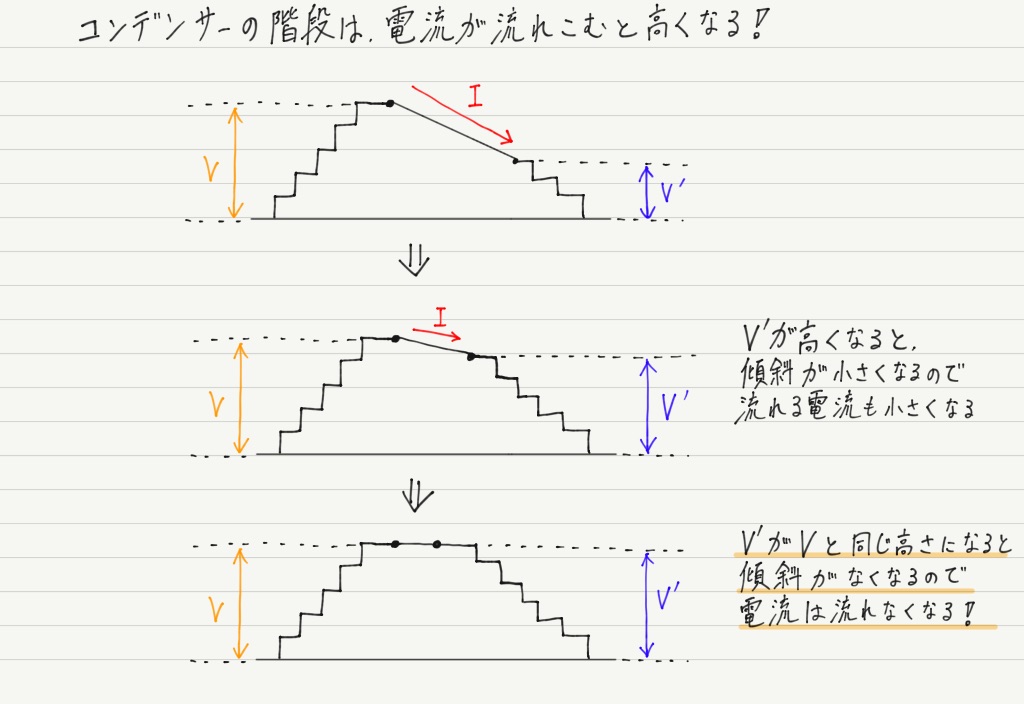
しかし電流が流れ込むにつれ,コンデンサーの“階段”はだんだん高くなります。
そして最終的に電池と同じ高さになるともう電流は流れません。
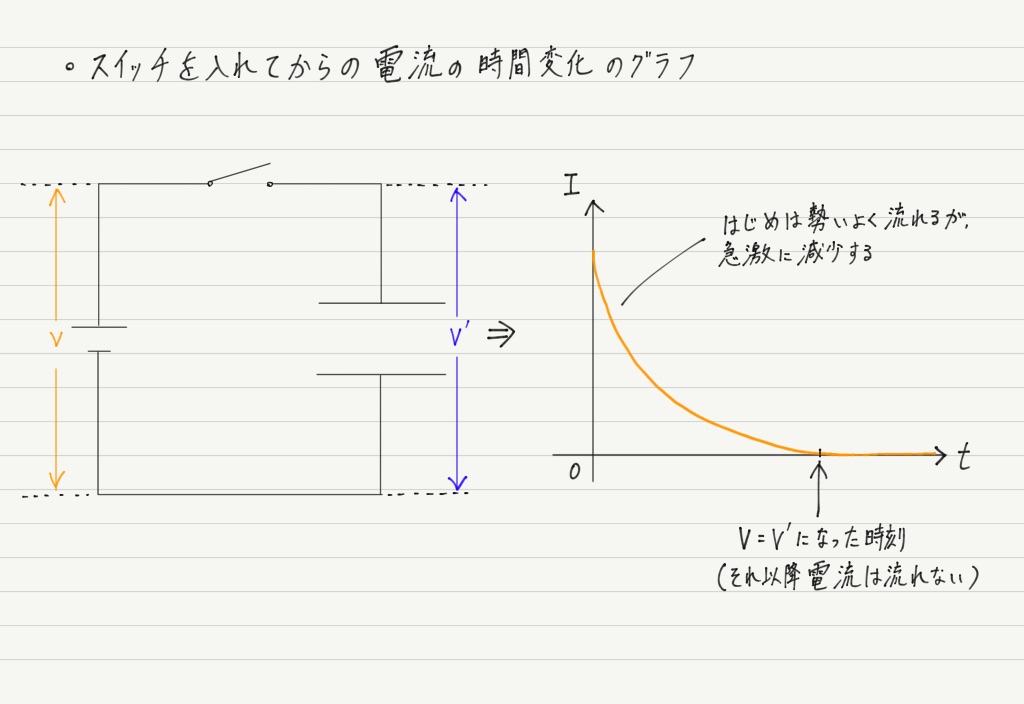
電池にコンデンサーをつないで,スイッチを入れてからの時間経過をグラフにしたものがこちら。
この “階段” の例え話がしっくり来なかった人は電圧を復習しておいてください。
コンデンサーの充電・放電
上で見たように,コンデンサーに電池をつなぐと電荷が移動し,電気量が蓄えられます。
これをコンデンサーの充電といいます。 コンデンサーを一言で表すと,「電荷をためておく装置」ですね!
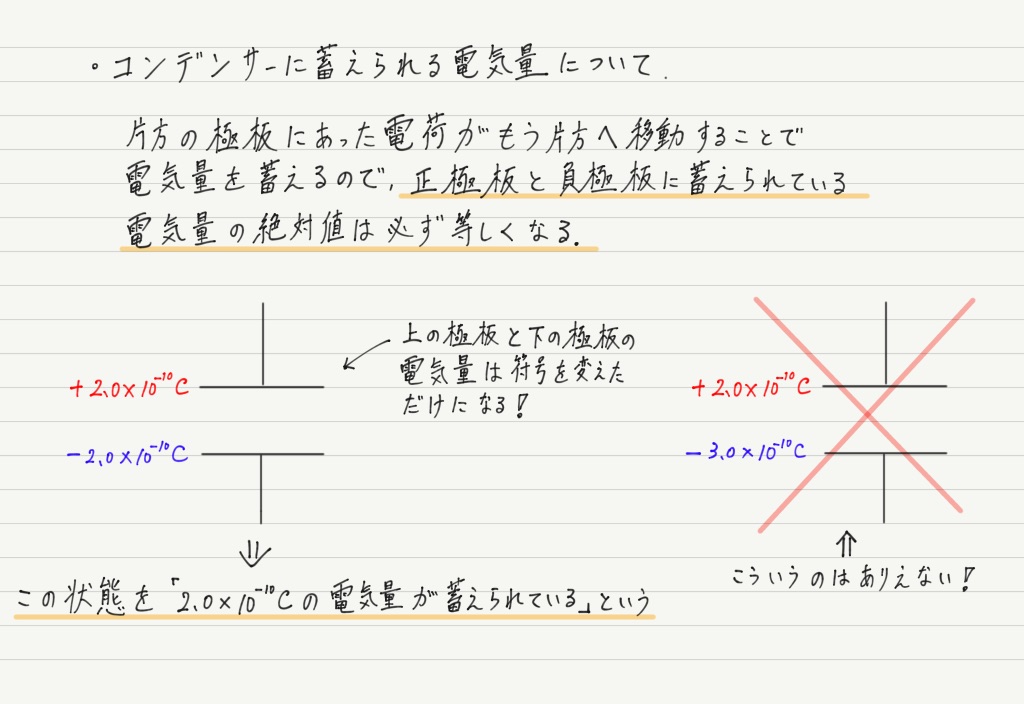
これから先,「コンデンサーに◯Cの電気量が蓄えられている」というような言い回しをよく使いますが,どういう状況なのかしっかり思い浮かべられるようにしておきましょう。
それから,グラフをもうひとつやっておきましょう。
・コンデンサーに電流が流れる→充電されている
・電流が流れなくなる→充電完了
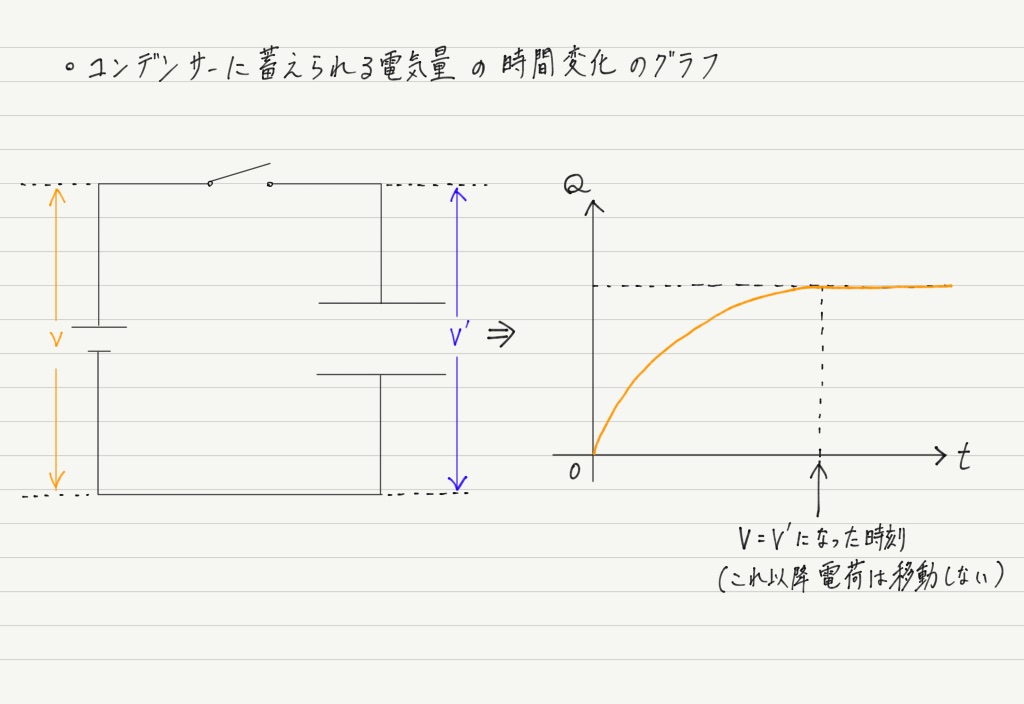
なので,スイッチを入れてからの経過時間と蓄えられる電気量のグラフは
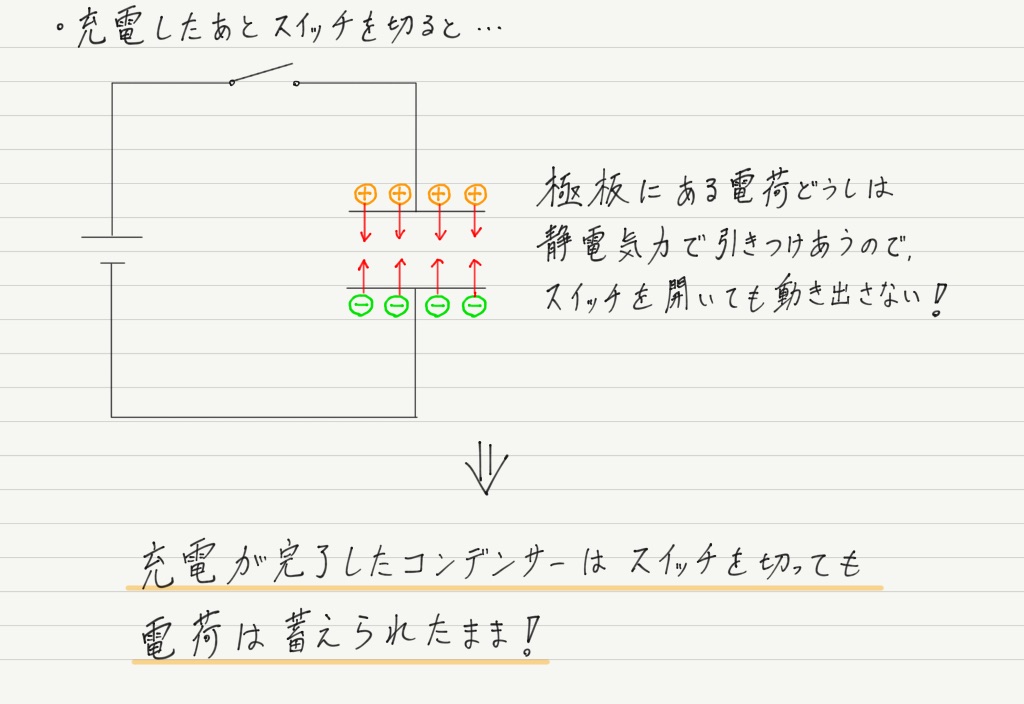
となります。 さて,充電が完了したあと,スイッチを切るとコンデンサーはどうなるでしょうか?
ちょっと考えてみてください。
それでは正解発表。
この性質は問題を解くときによく使うので,しっかり理解しておいてください!
ではいったんイメージの話に戻りましょう。
充電されたコンデンサーは“階段”のイメージなので,電池の役割を担うことができます。
イメージから連想されるとおり,この状態だと電流は高い方(正極板)から低い方(負極板)へ向かって流れます。
もちろん実際に移動しているのは自由電子で,充電のときに負極板に蓄えられた自由電子が,今度は抵抗を通って正極板に戻っているのです。
(上で説明したとおり,充電状態の極板の電荷は静電気力で移動できないが,導線で極板どうしをつなぐとそこが通り道になるので移動できてしまう。)
この現象をコンデンサーの「放電」といい,これは充電とは逆の現象です。
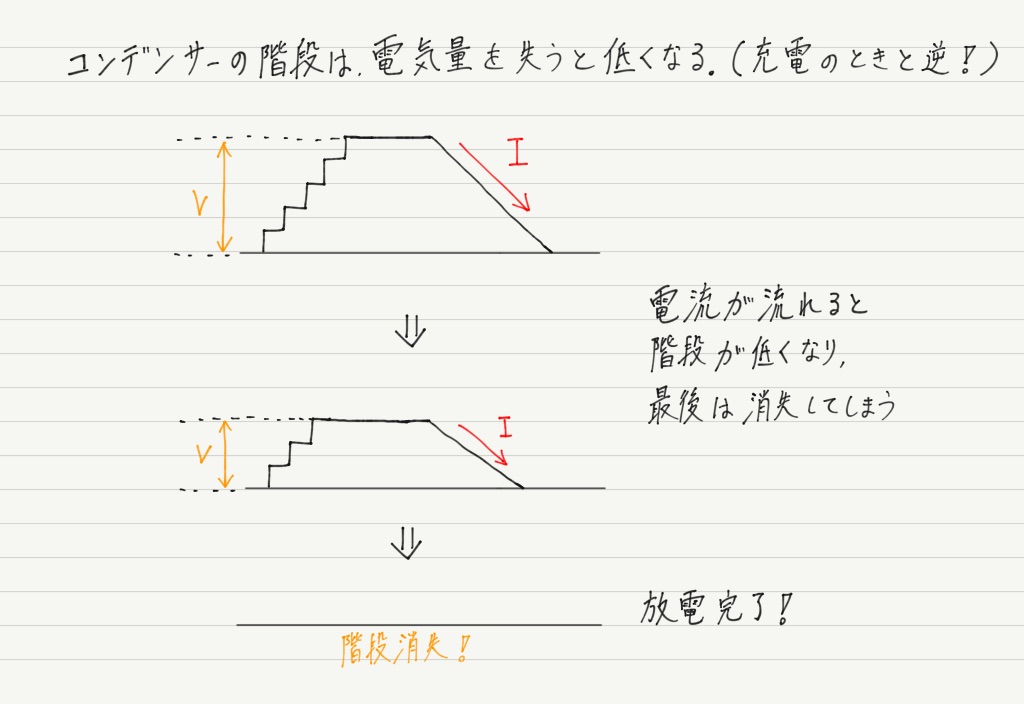
ところがこの放電は長く続かず,一瞬のうちに完了します
なぜなら放電によって蓄えられた電荷が放出されると,コンデンサーの “階段” はまたたく間に低くなってしまうからです。
こうして放電を終えたコンデンサーは再び充電することが可能になります。
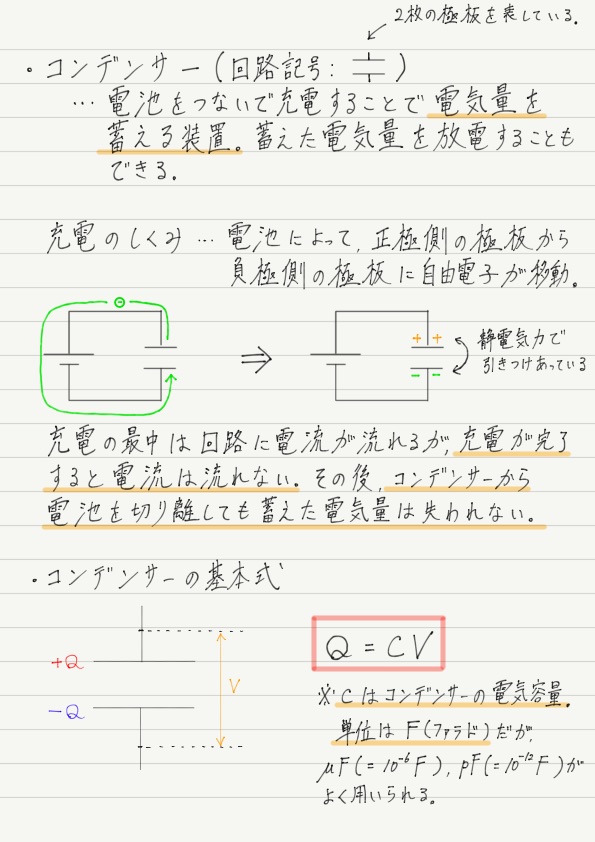
コンデンサーの基本式
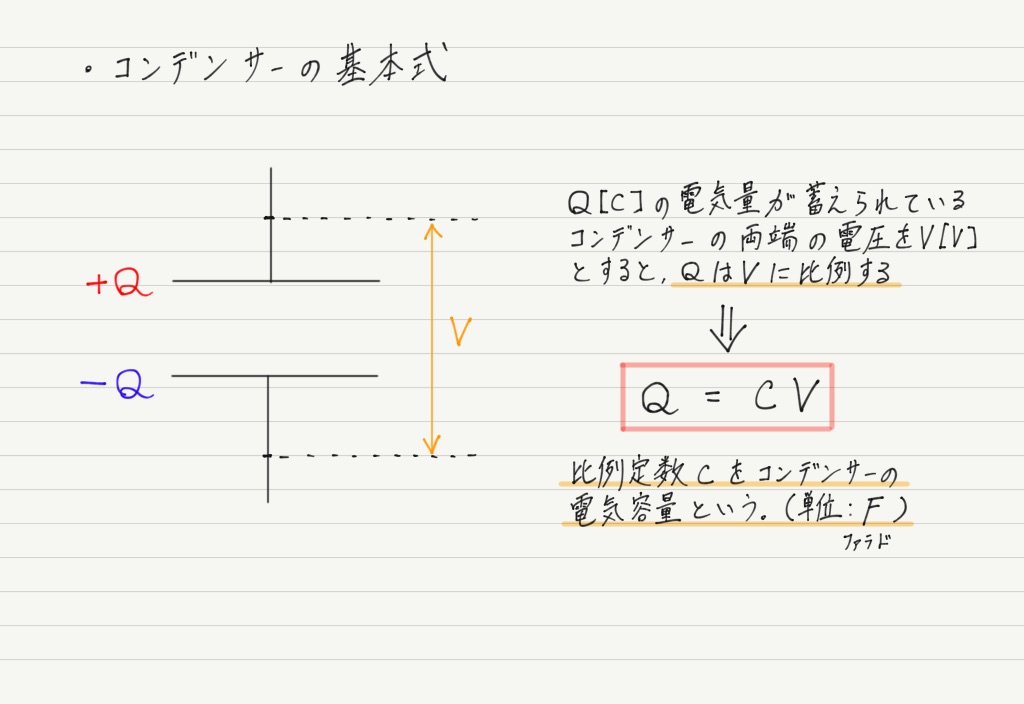
最後に,コンデンサーの問題を解く上でもっとも基本となる関係を紹介します。
その関係とは,「コンデンサーに蓄えられた電気量と,極板間の電位差は比例する」というものです。
電気容量とはその名の通り,コンデンサーにどれぐらい電気量をためることができるのかをあらわす指標です。
(電気容量が大きいほど,同じ電圧でより多くの電気量を蓄えられる)
ただし,1Fという単位は実用的には大きすぎる単位なので,μF(マイクロファラド)やpF(ピコファラド)を用いるのが一般的です。 電気容量についてはまた次回触れる機会があるので,詳しい説明はそのときに改めてしたいと思います。
今回のまとめノート
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。
次回予告
今回サラッとしか触れませんでしたが,充電されたコンデンサーの極板間には電場が存在しています。
そこで次回は,これまでに学んだ電場についての知識をコンデンサーに適用してみましょう!