電荷どうしの間にはたらく力のことを,静電気力(クーロン力)と呼ぶのでした。
静電気力についての知識は今のところ,
・異なる符号の電荷の間には引力がはたらく
・同じ符号の電荷の間には斥力がはたらく
という,力の向きの話だけで止まっている状態です。
今回はそこから一歩前進して,静電気力の大きさを求められるようになることを目標に勉強していきましょう!
クーロンの法則
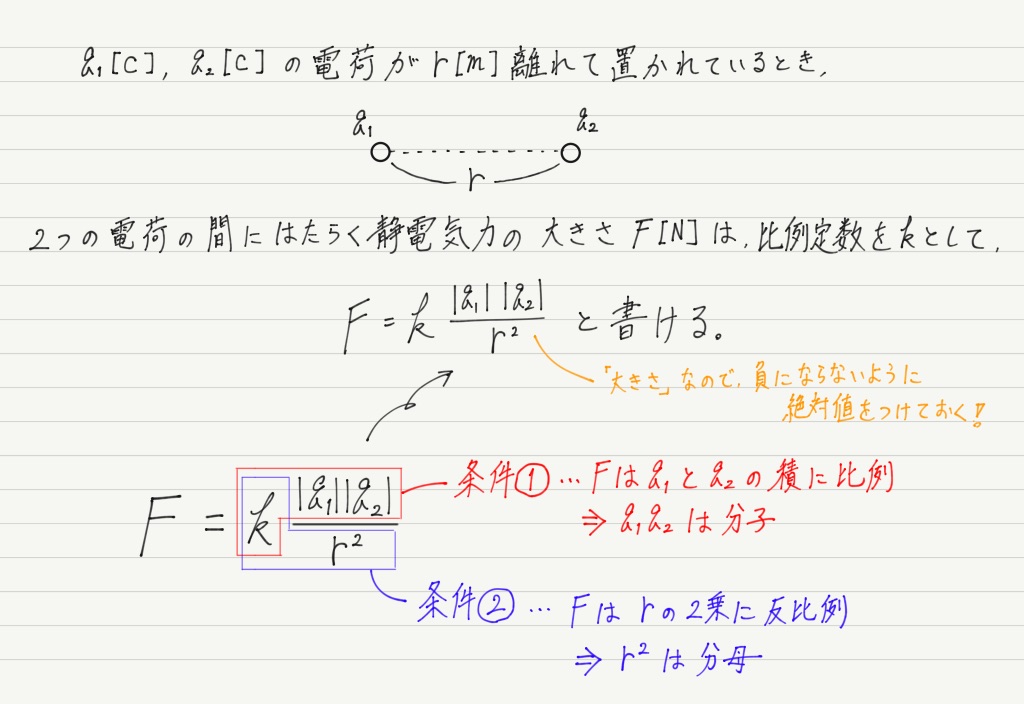
静電気力の大きさについて調べて,その規則を見つけた人物がクーロンさんです。 静電気力が別名クーロン力と呼ばれているのも,電気量の単位に名前が残っているのも,クーロンのこの業績を讃えてのこと…
…のハズですが,実際は色んな人が突き止めていて,初めて公に発表したのがクーロンだという話です。
まぁ,そういうゴタゴタはどうでもよくって(笑),肝心の中身について見ていきましょう。 クーロンが発見した事実は,
① 静電気力の大きさは2つの電荷の電気量の積に比例する。
② 静電気力の大きさは2つの電荷の距離の2乗に反比例する。
の2点です。 式で表そうとするとこんな感じになります。
比例定数kは「クーロン定数」と呼ばれており,電荷の間が何の物質で満たされているかによって値が変化します。
ここで注意点。 多くの教科書では,クーロンの法則は絶対値をつけない形で書かれています。
絶対値をつけない場合,2つの電荷が同符号ならFは正,異符号ならFは負になるので,
F>0 → 斥力
F<0 → 引力
を表していると解釈します。
…が,向きを符号で表したからと言って特別便利になるわけではありません。
そもそも計算なんかしなくても,引力か斥力かは2つの電荷の種類が分かればすぐに判断できるわけで。。。
そんなわけで,このサイトでは今後も大きさと向きは完全に分けて説明していきます!!
今回のまとめノート
クーロンの法則は「とりあえずこれに代入して計算すれば静電気力の大きさがわかる」というもので,これ以上でもこれ以下でもありません。
なので今回はこれでおしまいにしますが,このあとの記事でクーロンの法則に形が似た式がいくつか登場します。
うろ覚えだと混乱してしまう恐れがあるので,式の形だけはちゃんと覚えておきましょうね!
演習問題も用意してあるのでチャレンジしてみてください!
次回予告
今回は式の紹介だけの軽めの話題でしたが,次回は一転して電磁気分野の最重要概念である「電場」が登場します。
決して難しいわけではありませんが,心してかかってください。