円運動のところでも触れましたが,地面に落ちるりんごを見たニュートンは「月にも同じ力がはたらいていて,りんごと同じように落ちているのではないか?」と考えたそうです。嘘くさい。
りんごは地球に引かれて落ちる。 月も地球に引かれて落ちる(=公転する)。
りんごや月に限らず,すべてのものは地球に引っ張られているのではないか?
すべての物体を引っ張る力,その正体とは一体!?
万有引力の法則
その力こそ,誰でも一度は耳にしたことがあるであろう,万有引力です!
引力だけに冒頭で大げさに引っ張りましたが(激ウマギャグ),そんなに面白い話があるわけでもなく,万有引力の大きさを求める公式を紹介するぐらいしかやることがありません。
というわけで,その公式をどうぞ!
“お互いに” 引き合うというのがポイント!
我々は普段地球に引っ張られて生活していますが,逆に同じ力で地球を引っ張っている(!)のです。
ところで,万有引力はその名の通り「すべての物体の間にはたらく力」。
冒頭で「地球とりんご」「地球と月」の話をしましたが,何も片方が地球である必要はありません。
月とりんごの間にも万有引力ははたらいているし,今これを読んでいるあなたとそこら辺に落ちているティッシュの間にも万有引力はたらいています。 まったくそんな力は感じないけど。
そこら辺の物体との間の万有引力を実感できないのは,万有引力定数Gが非常に小さいためです。
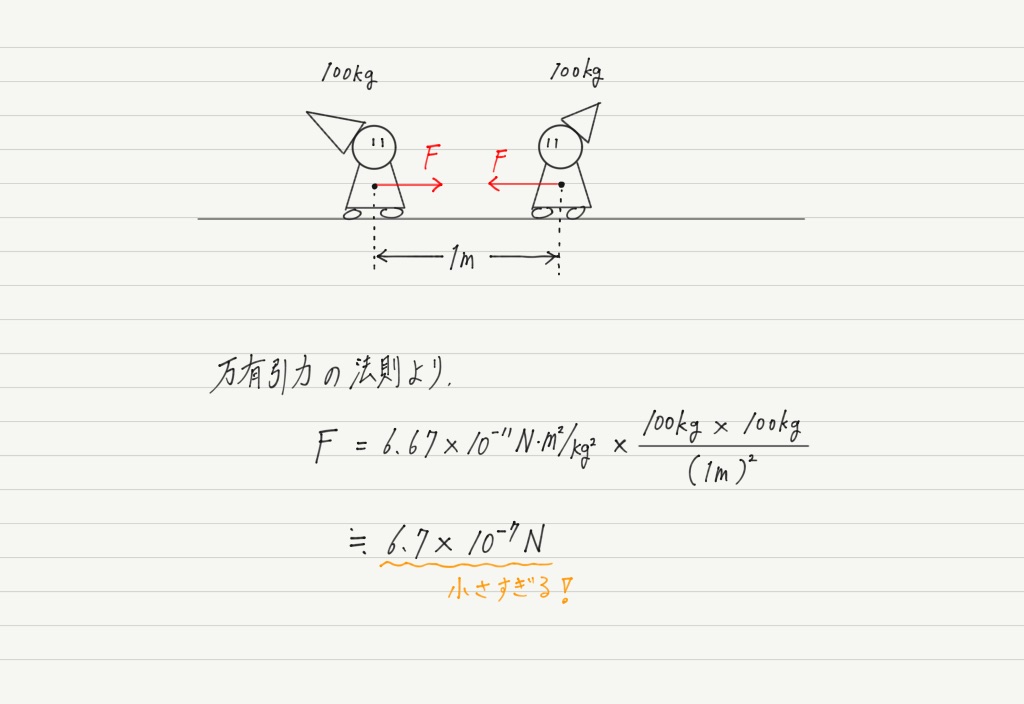
体重100kgの人どうしが1m離れているとして,その2人がお互いに及ぼす万有引力の大きさを求めてみます。
というわけで,基本的に「万有引力=めっちゃ小さい」というイメージでOK。
2物体の衝突のような普通の力学の問題では物体間にはたらく万有引力なんか考えませんよね?
考えなかった理由はまだ万有引力を習っていなかったからではなく,万有引力が小さすぎて無視できるから。
しかし,2つの物体のうち少なくとも一方の質量が惑星レベルに大きい場合はさすがに万有引力の影響が無視できません。
“万有” 引力と呼んでおきながら,惑星の問題でしか出てこないのはこういう事情なのです。
重力と万有引力
地球から受ける万有引力のことを重力と呼ぶ,と思っている人が多いですがそれは正確ではありません。
地球上の物体が地球から受ける力は2種類あります。
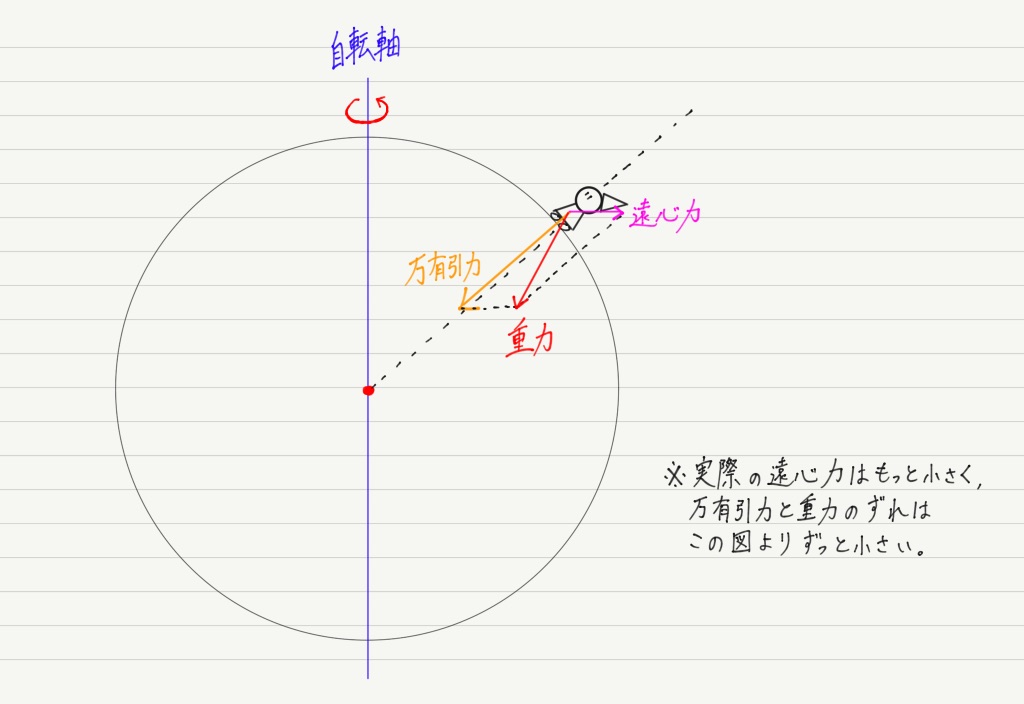
1つは万有引力。 もう1つは地球の自転による遠心力。
この2力の合力が重力です。
…とは言うものの,遠心力の大きさは万有引力に比べてかなり小さいので,無視することがほとんど。
結局は,「重力とは,地球から受ける万有引力と遠心力の合力のことだけれど,計算上は地球から受ける万有引力のことだと思ってよい」ということです。 ややこし!
最後にひとつ計算してみましょう。
一旦読むのをやめて自力で解いてみてください。
解けたら画面をスクロールして答え合わせ!
では,解答です。
(3)で求めたgとGの関係式はよく使うので,いつでも求められるようにしておきましょう!
今回のまとめノート
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。
次回予告
自転の遠心力を無視すれば重力と万有引力は同じもの。
重力には位置エネルギーがあったのだから,万有引力にも位置エネルギーがあるはず…?