単振動の基本的な知識が身についたところで,いよいよ具体的な運動を取り扱ってみましょう。
例題を解きながら解説していきたいと思います!
例題
この問題の設定のように,水平に設置したばねにつながれた物体の運動は水平ばね振り子と呼ばれます。
ここまで習った知識だけで十分解けるレベルの問題なので,やる気のある人は一旦読むのをストップしてがんばって解いてみてください!
全然解ける気がしないという人は解説へGO!
解答・解説
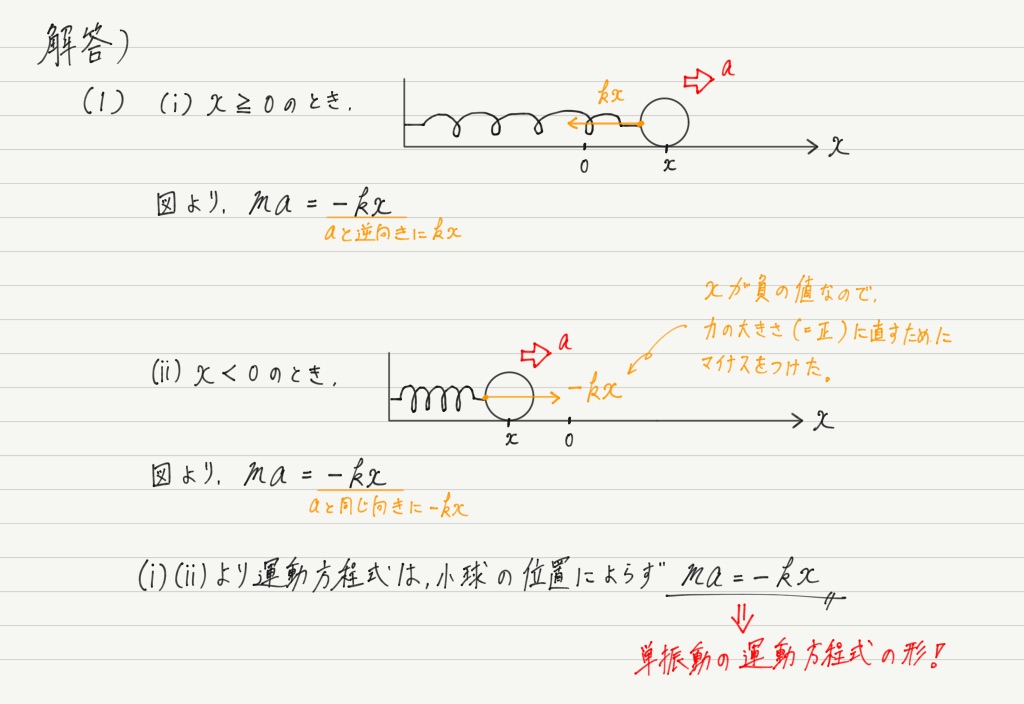
ではまず(1)の解答からいってみましょう。
(※ 問題でx軸の向きが決められているので,aの向きもそれに従う。)
最初なので分かりやすくxが正の場合と負の場合に分けて求めましたが,実際の問題では場合分けして答える必要はないでしょう。
見てのとおり,どちらにしても同じ形の運動方程式が得られるからです。
さて,得られた運動方程式の形に注目!!
見た瞬間に「単振動の運動方程式 ma = −Kx とまったく同じ形をしている!」とピンときてください!
てことは,水平ばね振り子の運動は単振動になるんですねぇ。
…まぁ,ばねにつながれてるので,伸びたり縮んだりしながら振動するに決まってるんだけど。
では続いて(2)。
振幅は変位の最大値のことですが,今回の問題のように最初に物体を引っ張って(あるいは押し縮めて)運動を開始させた場合,最初に引っ張った(or 押し縮めた)長さ以上に大きく振動することは決してありません!
よって,振幅は特に計算することなく求められます。
周期の方は計算して求める別解も用意しましたが,周期の公式のKを復元力の比例定数に置き換える方法のほうが絶対簡単です(推奨)。
最後に(3)です。
後半の力学的エネルギー保存則はおまけなので特に言うことはありません。
注意してほしいのはこの前半の時刻を求める問題。 単振動の問題で時間を問う問題は少なくありません。
そして,「どの公式を使って求めるんだろう??」と頭をかしげる人も少なくありません。
しかし! 単振動の時間を求める問題で悩むのはナンセンス!!
確かにこれまでも力学で時間を求める問題はたくさんあったし,時間を求めるのに使えそうな公式もありました。
でもそれって等速度,もしくは等加速度の話ですよね!?
単振動は等速度でも,等加速度でもありません。 すると,使える公式なんてないも同然。
単振動について我々が知っている時間の情報はただひとつ,周期だけ。
よって,単振動の問題で時間について聞かれた場合は,周期の何倍かを考えるしかないのです!!
(逆に言えば,周期の何倍かで答えられる問題しか出ない!)
これさえ知っておけば,今後時間の問題に出会っても何も悩む必要ナシ。
この解答のように即座に円運動に置き換えて,周期の何倍かだけを考えるようにしましょう。
今回まとめノートはありません(次回のまとめノートに今回の分も一緒に書きます)が,演習問題は作ってあるので是非チャレンジしてみてください!
次回予告
単振動の例が水平ばね振り子だけでは物足りないので,もう1つ具体例を紹介します!