今回から高校力学最大の難関（？），単振動に突入します！
と言うと，また新しい運動をイチからやるように聞こえますが，それは半分正解で半分ハズレ。
新しい運動にはちがいないけれど，内容は円運動からの続きとなります。
円運動が不安という人は復習しましょう。
円運動がバッチリな人は，さっそく単振動へ！
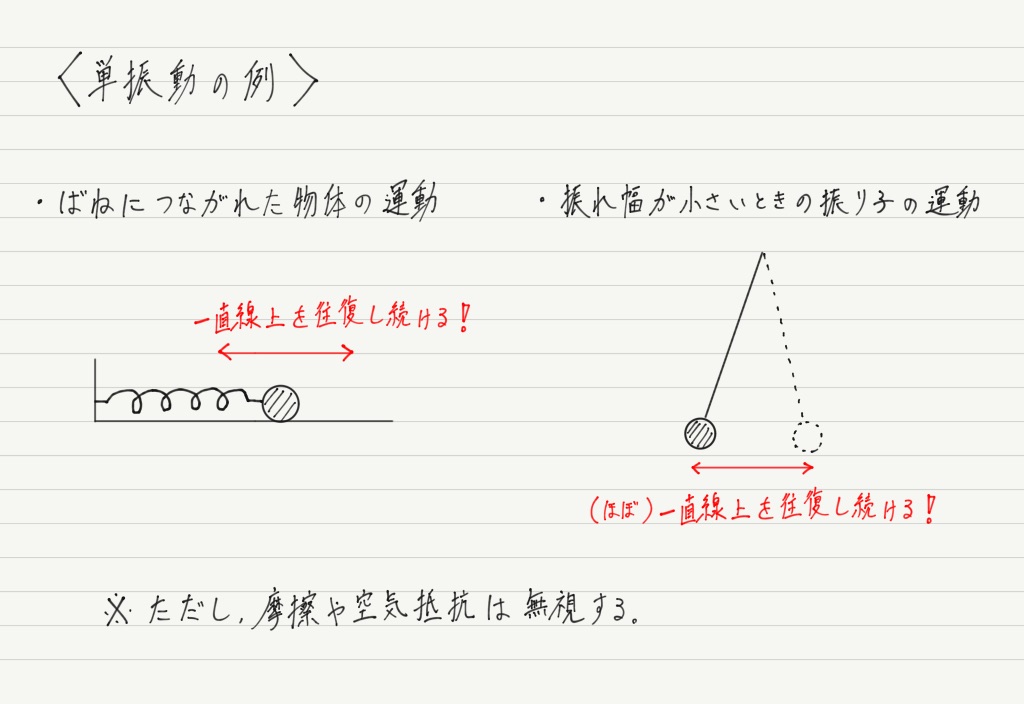
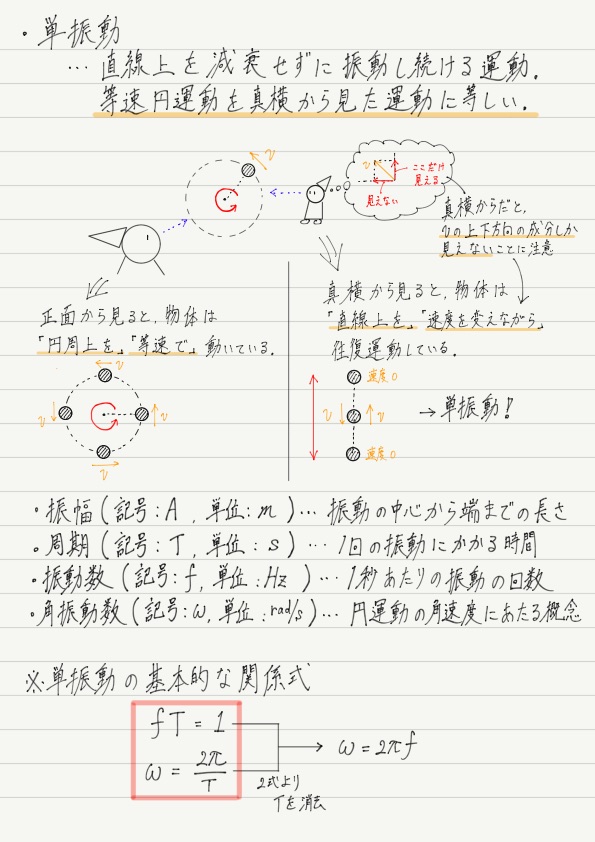
単振動とは
一口に振動といっても，その運動はいろいろ考えられますが，ここでは単純に一直線上を往復し続ける運動だけを考えます。
単純な振動，略して単振動というわけです。
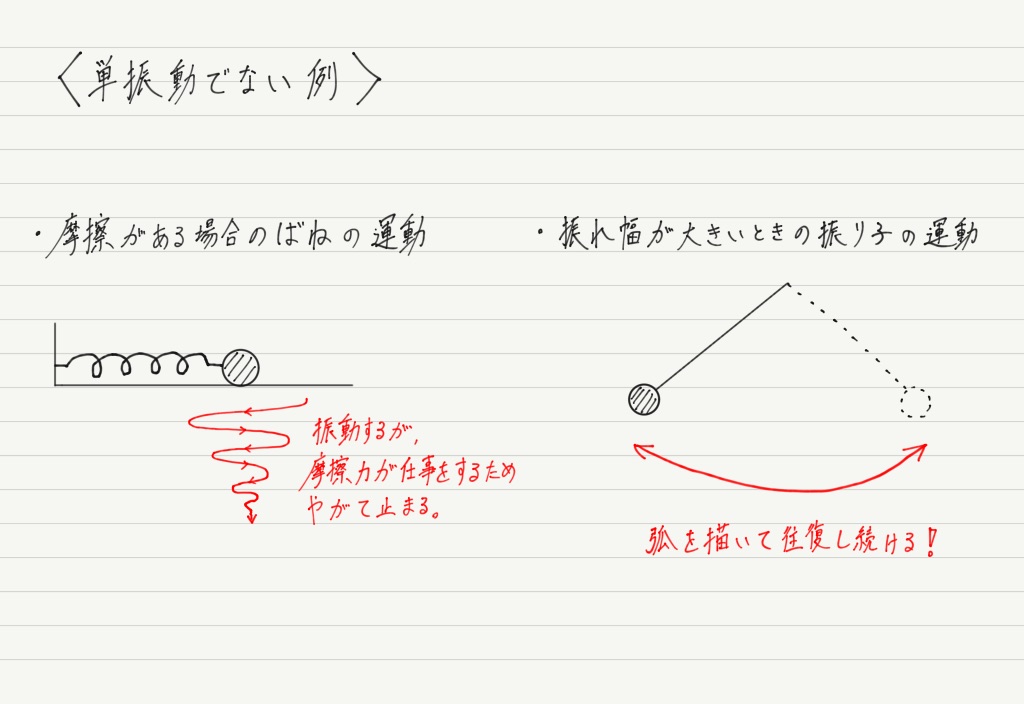
高校の物理では扱いませんが，単振動じゃない振動も紹介しておきますね！
さて，単振動は運動の様子を見る限りはそんなに難しくなさそうなのですが，計算しようとするとちょっと厄介。
単振動は加速度運動ではあるけれど，等加速度運動ではないからです！
…どうしよう？(・・;)
等速円運動と単振動の共通点
そう言われると一気に難しく感じる単振動ですが，ご安心ください！
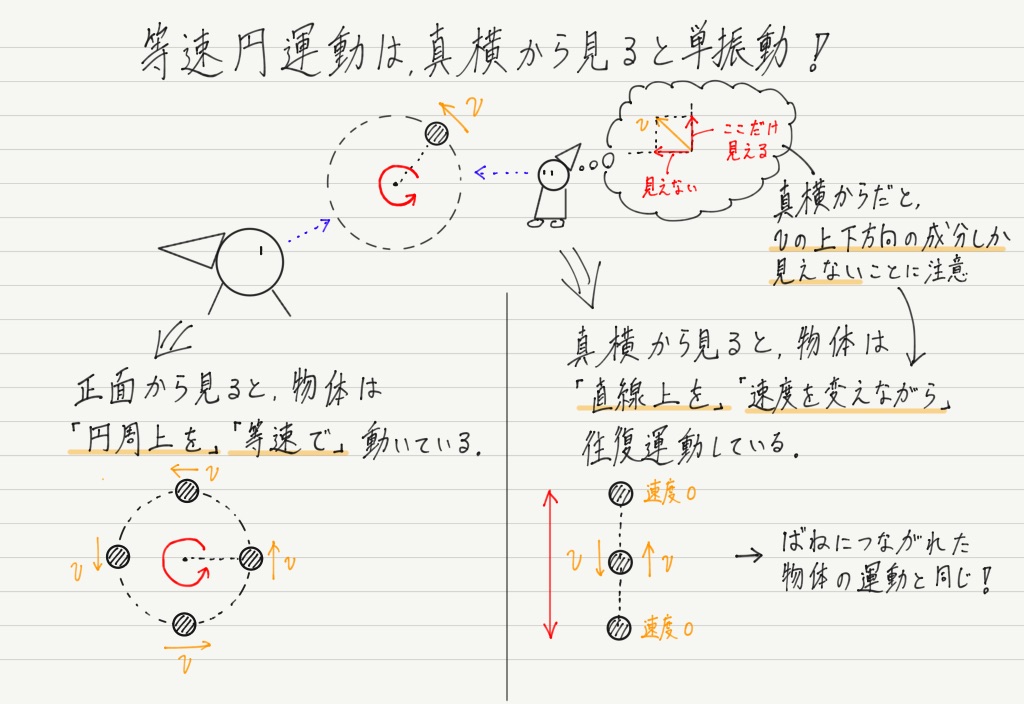
なんと単振動は等速円運動と本質的に同じであることが知られています。
「いや，ぜんぜんちがうやんけ！」ってつっこみたくなりますが，等速円運動を真横から見ると，なんと単振動と見分けがつかないのです！！
（波の分野を最初に見た人にとっては復習ですね！）
見る方向を変えただけなので，単振動を調べる代わりに等速円運動を調べても結果は同じ。
よって，物理量や公式も基本的にそのまま使えることになります（物理量は呼称が変わるものもあり）。
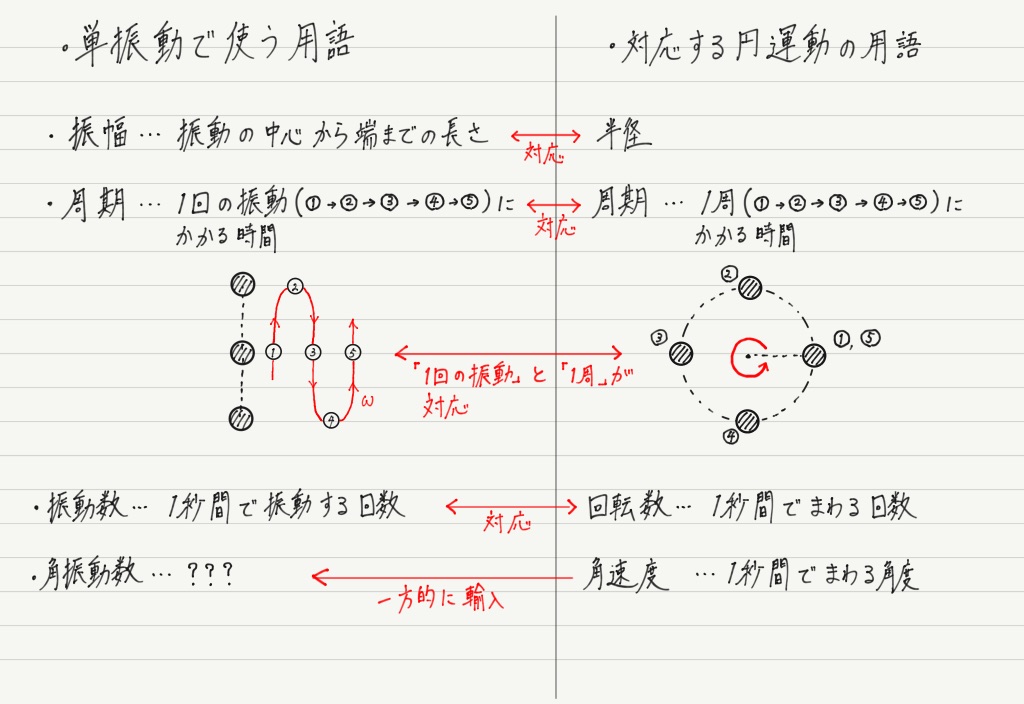
やはり一番下の角振動数の？？？が気になると思います。
円運動で角速度という概念が非常に便利だったので，そのまま単振動でも使おう！という発想のもと，輸入された概念が角振動数。
ところが，単振動では「角度」という概念がないので，単振動の言葉に置き換えられません。 よって？？？なのです。
公式もどうぞ。
一番下の公式より，f を2π倍したものが角振動数ωであることがわかります。
さっきは？？？として説明を放棄した角振動数ですが，この関係を使えば，「角振動数とは，2π秒間で振動する回数である」と意味付け可能です。
が，2π秒っていうのがそもそも意味不明だし，実際のところωは，「f の代わりにωを使うと式が簡単に表せたりして便利だよね」くらいのニュアンスでしか用いられません。
「角振動数は言葉では説明しにくいけれど，円運動と同様の公式が成り立つものとして扱う」と割り切ってしまうのが正解だと思います。
ちょっと話が長くなってしまったので，これ以降は次回に持ち越しましょう。
今回のまとめノート
時間に余裕がある人は，ぜひ問題演習にもチャレンジしてみてください！ より一層理解が深まります。
次回予告
運動を調べる上で欠かせないのはやはり速度と加速度。
これまた円運動をヒントにして調べていきます！
