「バスが急停止すると,中にいる乗客は前方にバランスを崩す」
という現象は慣性の法則の例としてよく挙げられますが,この現象がなぜ起こるのか説明できますか?
今回はこの現象を “2つの視点” から解明していきます!
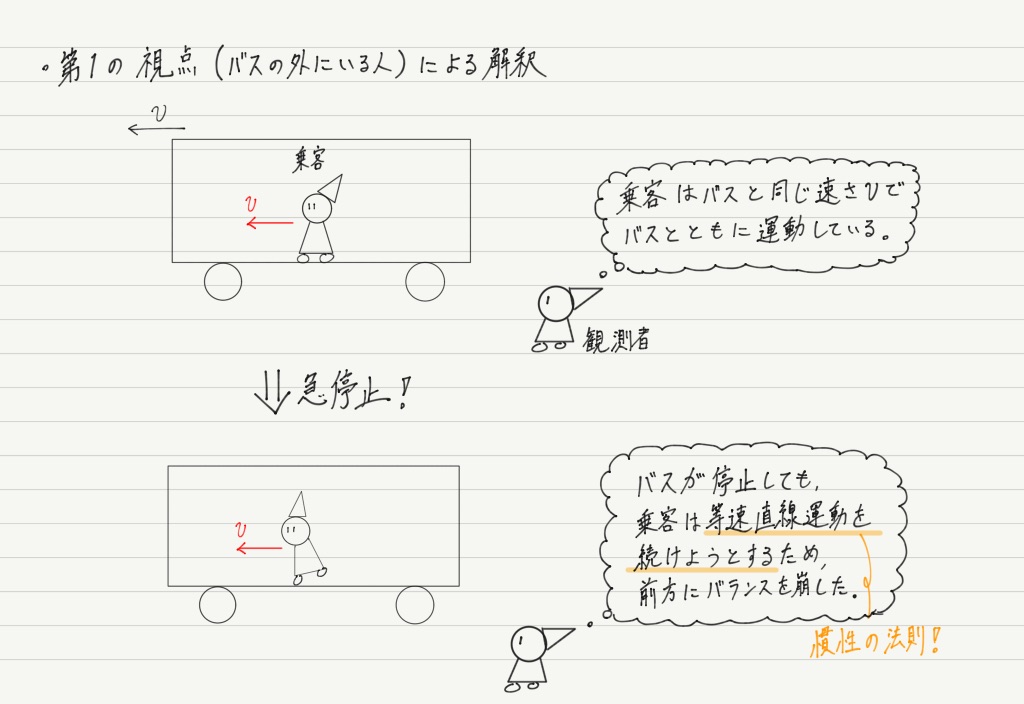
第1の視点 〜外にいる人の解釈〜
バスの乗客がバランスを崩す様子をバスの外から見た場合,次のように解釈できます。
ポイントはもちろん慣性の法則。
この現象は,「運動している物体は,力がはたらかなければ等速直線運動をする」ということの具体例に他なりません。
第2の視点 〜バランスを崩した本人の解釈〜
第1の視点については物理基礎の慣性の法則の記事でも説明済みなので,今回のメインテーマはこちらの第2の視点のほうです。
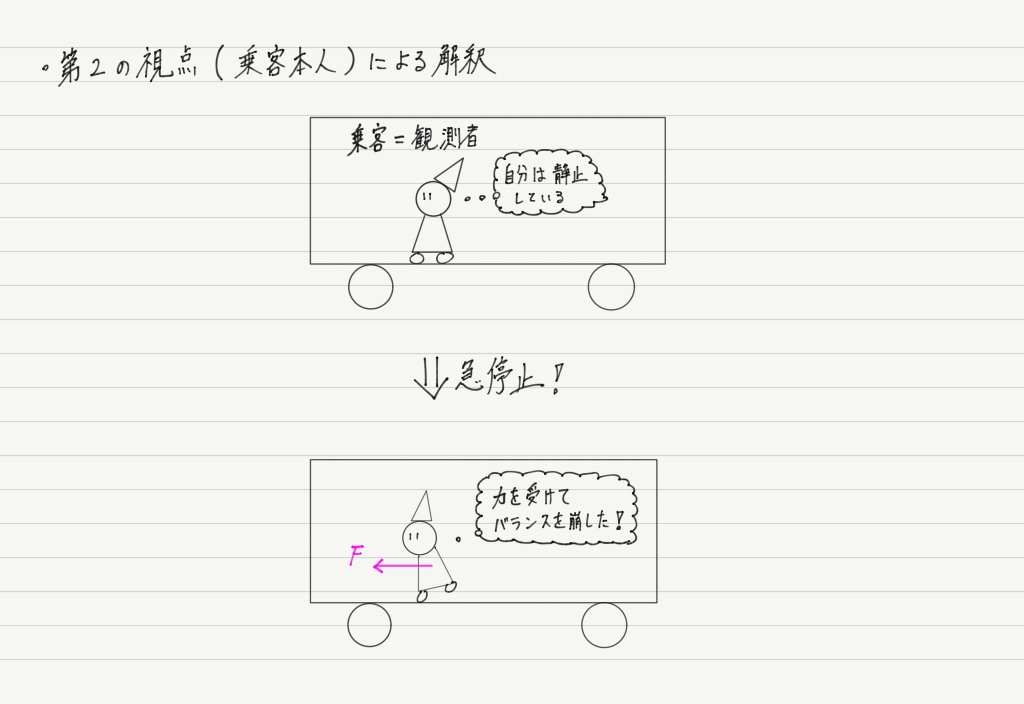
「車内でバランスを崩した」という現象を,バランスを崩した張本人はどう解釈すればいいのでしょうか?
注意すべきは,第1の視点と同じ解釈は使えないということ。
第1の視点の解釈では,「バランスを崩す前,バスは運動をしている」というのが前提でした。
しかし,中にいる人は「自分とバスは静止していて,動いているのは外の風景のほうだ」と主張できます(相対速度の考え方!)。
「自分ではなく外が動いている」という考え方は慣れていないと奇妙に映るかもしれませんが,がんばって受け入れてください。
ともあれ,「自分は止まっているんだ」と考えて,慣性の法則「静止している物体は,力がはたらかなければ静止したまま」を適用すると,ひとつの結論が導かれます。
乗客「自分はもともと静止していたのだから,力がはたらかなければ静止し続けるはず。
にも関わらずバランスを崩したということは,何か力がはたらいたことになる!」
うん,名推理。
乗客にはたらいたこの謎の力は慣性力と呼ばれています。
つまり,第2の視点からの解釈は単純に,「前方にバランスを崩した理由は,慣性力で前向きに引っ張られたから」ということになります。
慣性力は “見かけの力”
この慣性力という力ですが,第1の視点(外にいる観測者)のときには登場していないことに注意してください!
外にいる人にとっては存在しないけれど,バスの中の人には確かに感じられる力…。
これって前回の遠心力と似てますよね!?
そうです! 遠心力と同様,慣性力も “見かけの力” なのです!
前回で円運動が終わって,何で今回急に慣性の法則の話をはじめたのか疑問に感じた人もいると思いますが,こういうつながりだったわけです。
遠心力の特徴に,観測者の立場によってあったりなかったりする,何から及ぼされる力なのか不明,反作用が存在しない,というものがありましたが,これらの性質はすべて慣性力にも当てはまります。
慣性力の向きと大きさ
慣性力は見かけの力とはいえ,力であることに変わりはないので,向きと大きさについてチェックしましょう。
…とその前に,慣性力について正確に説明しておきましょう。
慣性力とは,「加速度運動している観測者が感じる見かけの力」のことです。
さっきから「バスの中の観測者」とばかり言っていますが,バスの中にいるからといって常に慣性力がはたらいているわけではありません。
慣性力を感じるのは,急発車 or 急停止時に限られます。
これって加速度運動しているってことですよね!
もちろん乗り物はバスじゃなくても構いません。
加速度運動さえしていれば電車や飛行機,エレベーターでも慣性力ははたらきます。
(上昇するエレベーターが止まるとき,体にフワッと感じるのが慣性力!)
では本題。 慣性力の向きですが,これはまたバスの中を想像してください。
乗客はバスが急停止すると前方に,急発車すると後方にバランスを崩します。
これは慣性力の向きが加速度と反対方向であることを示しています!
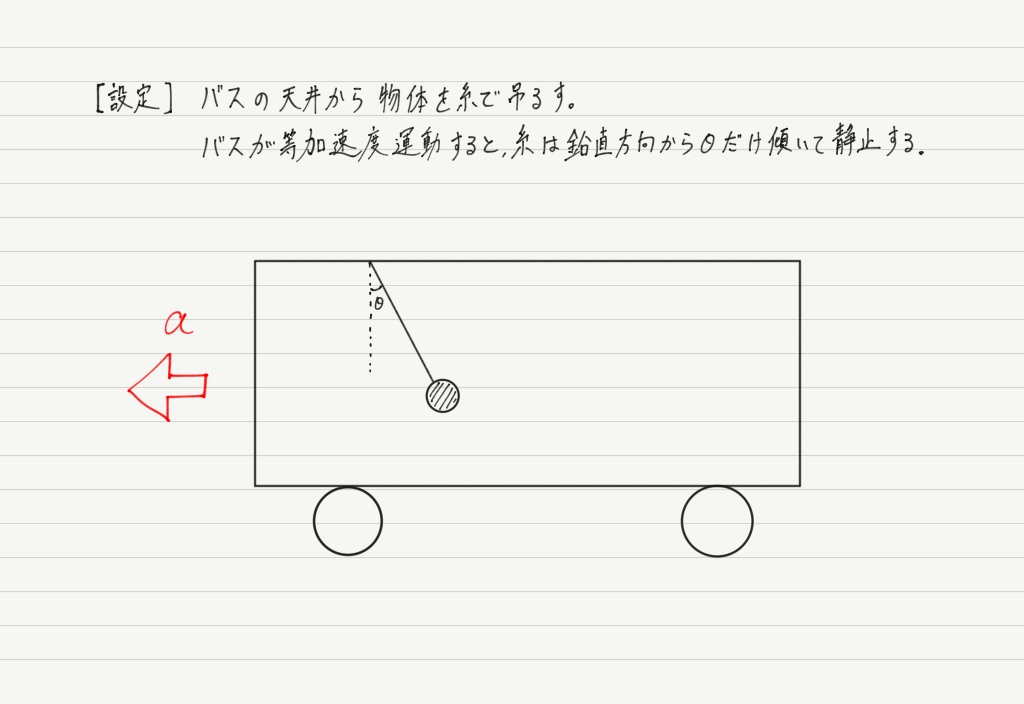
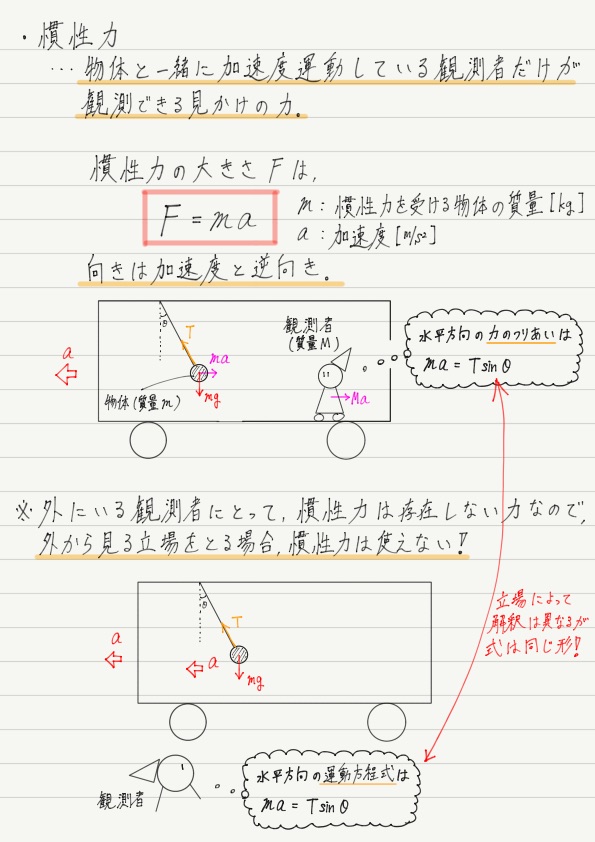
次に慣性力の大きさを求めてみましょう。 以下の図をご覧ください。
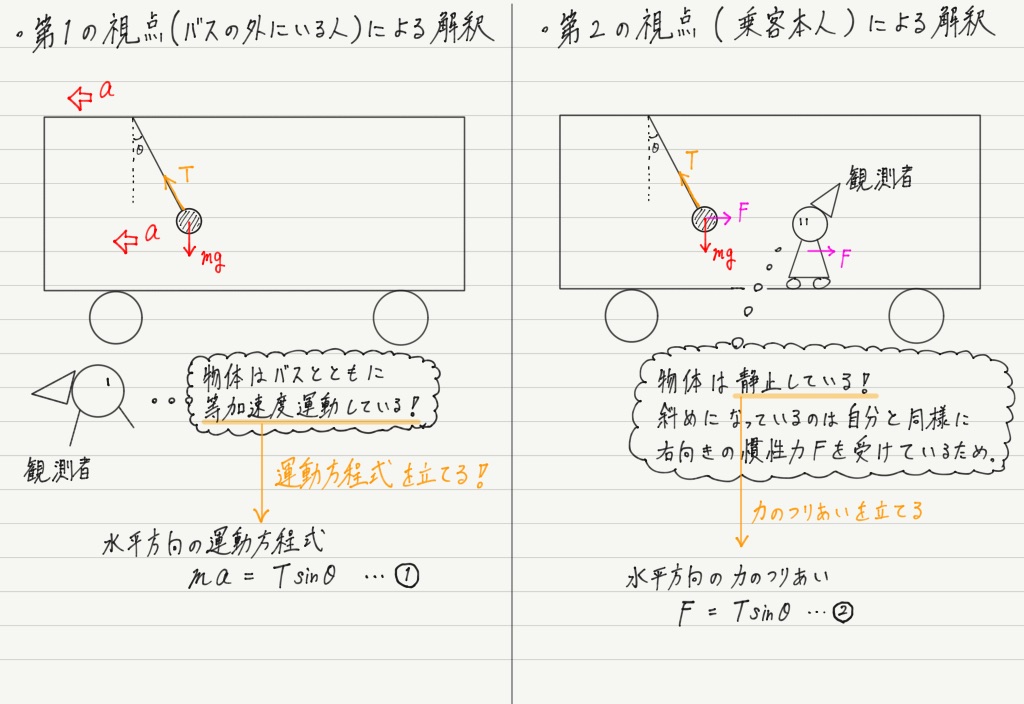
これを第1の視点と第2の視点からそれぞれ立式してみます(前回の遠心力のところでも似たような例題をやったことを思い出しましょう)。
第1の視点から見たときには慣性力が存在しないこと,第2の視点からは物体が静止して見える(観測者に対する相対速度が0)ことに注意しましょう!
ここからもう少し話を進めてみると…
以上より,慣性力の向きは加速度と逆向きで,大きさはmaであることがわかりました!
(※ 教科書では慣性力について, F =−ma と表記されていますが,マイナスがついているのは逆向きであることを表しているだけで,慣性力の大きさ自体はmaです。)
まとめに入る前に種明かしをしておきたいと思います。
前回と今回で学習したことをそのまままとめると,
「円運動をしている観測者には遠心力,加速度運動している観測者には慣性力という見かけの力がはたらく」
ということになりますが,この2つを別々に覚えてはいけません。
もうすでに気付いた人もいるかもしれませんが,実は慣性力と遠心力は同じものだからです!
要するに,円運動のときの慣性力のことを遠心力と呼んでいるだけ。
バラバラに覚えるのではなく,統一して理解してください。
今回のまとめノート
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。
次回予告
いよいよ高校物理力学の最後の難関,単振動が登場します!