すべての運動は運動方程式によって記述される,という話を物理基礎のところでしましたが,当然円運動も例外ではありません。
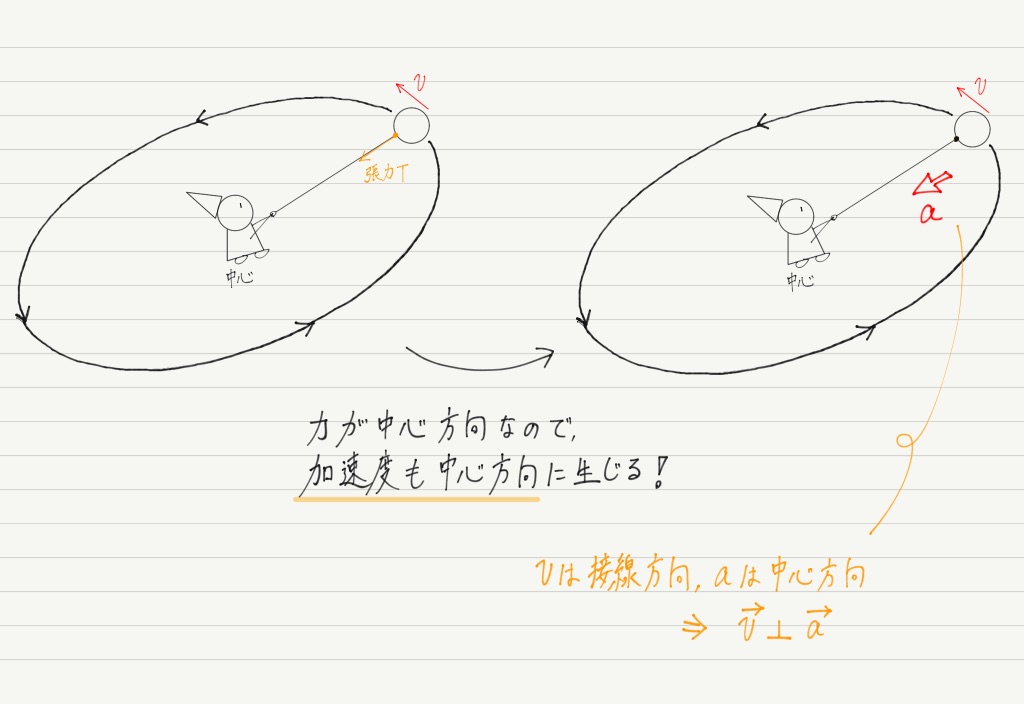
運動方程式の主役は力ですが,「物体が円運動をするためには中心方向へ向かう力が必要」ということが前回判明しました。
この知識を元に,今回は実際に円運動の運動方程式を立ててみましょう!
円運動の加速度
と,その前に。
運動方程式の主役は力だけではありません。 加速度だって主役級です。
そこで,まずは円運動の加速度について考えてみましょう。
加速度の大事なポイントは大きさと向きですが,運動方程式がしっかり頭に入っていれば,向きについてはすぐに答えを出せるはず。
・運動方程式 → 力が加わる方向に加速度が生じる
・円運動 → 中心方向に力がはたらく
この2つの事実から,円運動の加速度は中心方向という結論が導かれます!
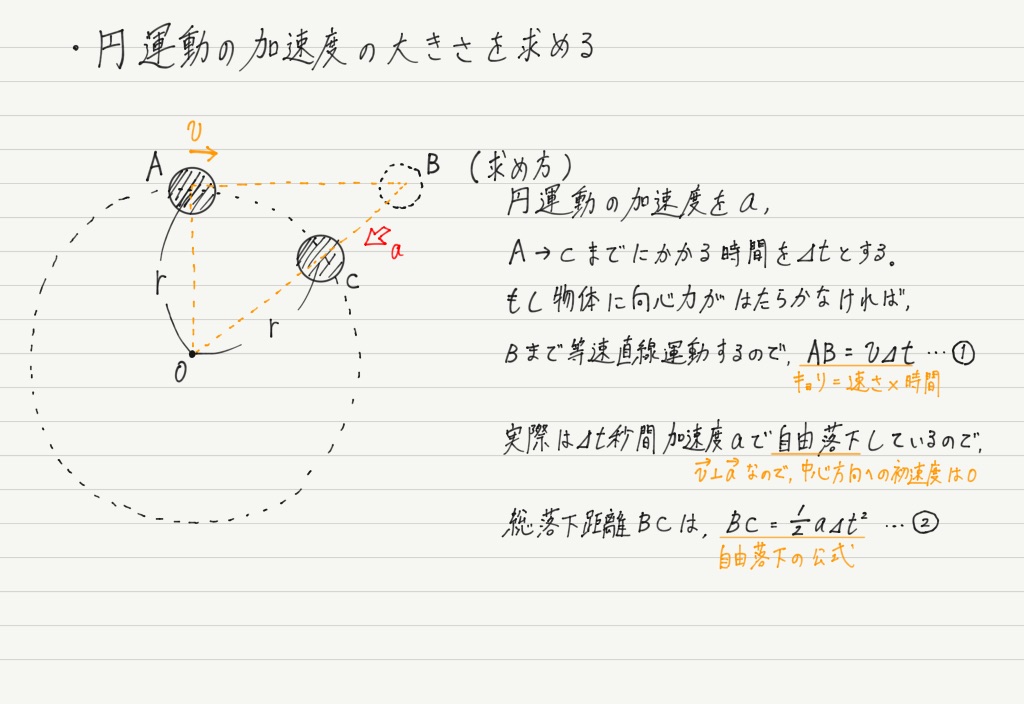
問題は加速度の大きさ。
前回扱った「円運動 = 中心への落下運動」というニュートンの考え方を利用して求めてみましょう。
これで円運動の加速度の大きさを計算することができました!
…が,ぶっちゃけ計算過程はどうでもよくて,最後の結果だけ公式として覚えてくれればOKです!
例題
それではお待ちかね,円運動の運動方程式を立ててみましょう。
今回はこの問題を解説しながら進めていきたいと思います。
まず(1)。「Aの直前」ということは,まだ円運動を開始していないということに注意しましょう。
ハイ,円運動全然関係ナシ(笑)
なぜこんな問題を入れたかというと,次の(2)と比較してもらいたいからです。
パッと見,(2)は(1)と何ら変わらないように見えますが,実は全然ちがいます。
(2)の小球はAを通過して円運動をはじめているので,重力と垂直抗力はつりあっていません。
(もしつりあっていたら,慣性の法則により,円運動ではなく等速直線運動をしてしまう!)
というわけで,ここで立てるべきはつりあいの式ではなく,円運動の運動方程式です。
直線運動の運動方程式は加速度を求めるために使うことが多かったですが,円運動の運動方程式はこのように,力を求める手段として使うことが多いです(加速度は公式で計算できてしまうので,運動方程式を使う必要がない)。
最後に(3)。
円運動の問題では運動方程式が必須なので,「図を描いて,加速度の向きと力の向きを確認する」という基本を徹底するようにしましょう。
途中でサラッと力学的エネルギー保存則も使っている点に注意。
すでに習った事項は必要なときにいつでも使えるようにしておきましょうね!
今回のまとめノート
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。
次回予告
次回は円運動にのみ現れる特別な力,遠心力について学習します!