力学は数回単位でコロコロ話題が変わっているイメージですが,またしても新しい分野に突入します。
今度のテーマは「円運動」。 その名の通り,円周上を動く運動のことです。
今回は初回ということで,円運動にまつわる用語を紹介していきたいと思います!
物体の速度と角速度
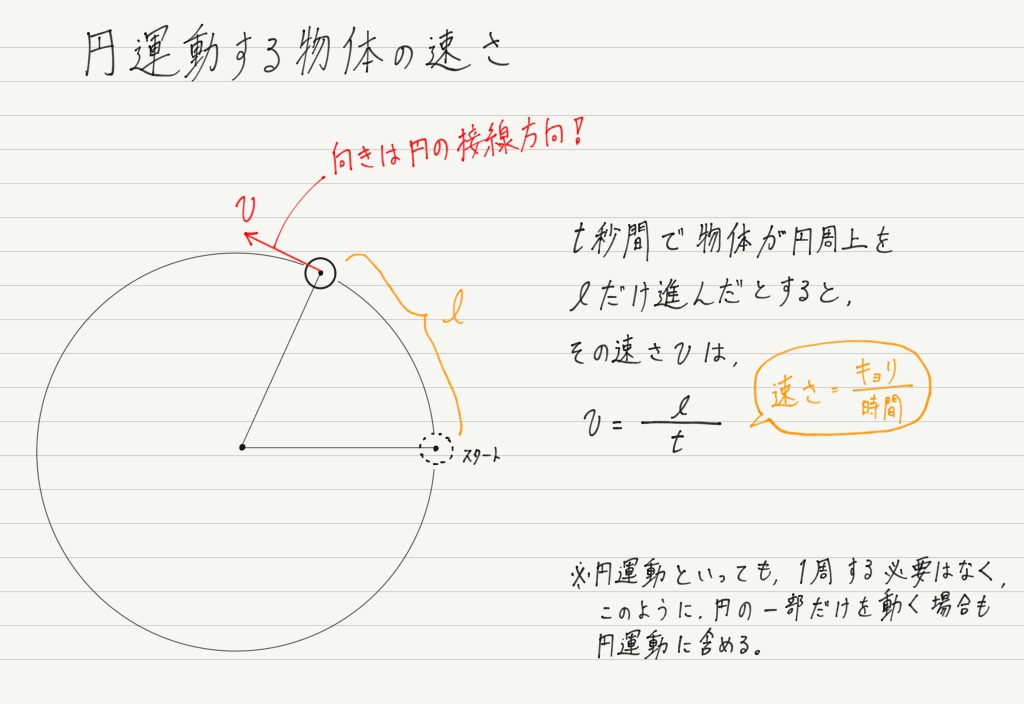
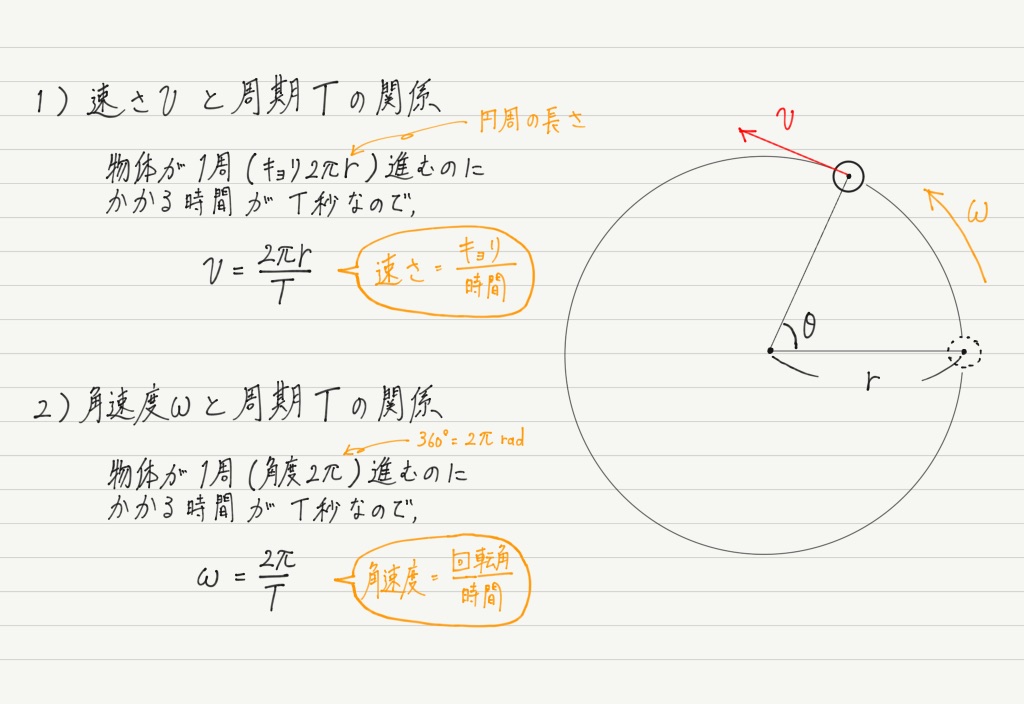
まずは円運動する物体の “速さ” について考えましょう。
とりあえずは円周上を一定の速さで運動する(=等速円運動)とします。
これはいつもどおり物体が進んだ距離をかかった時間で割ればいいですね!
これで終わりかというと,そうではありません。
おなじみの概念である「速さ」ですが,円運動を扱うにはちょっと微妙な点があるのです。
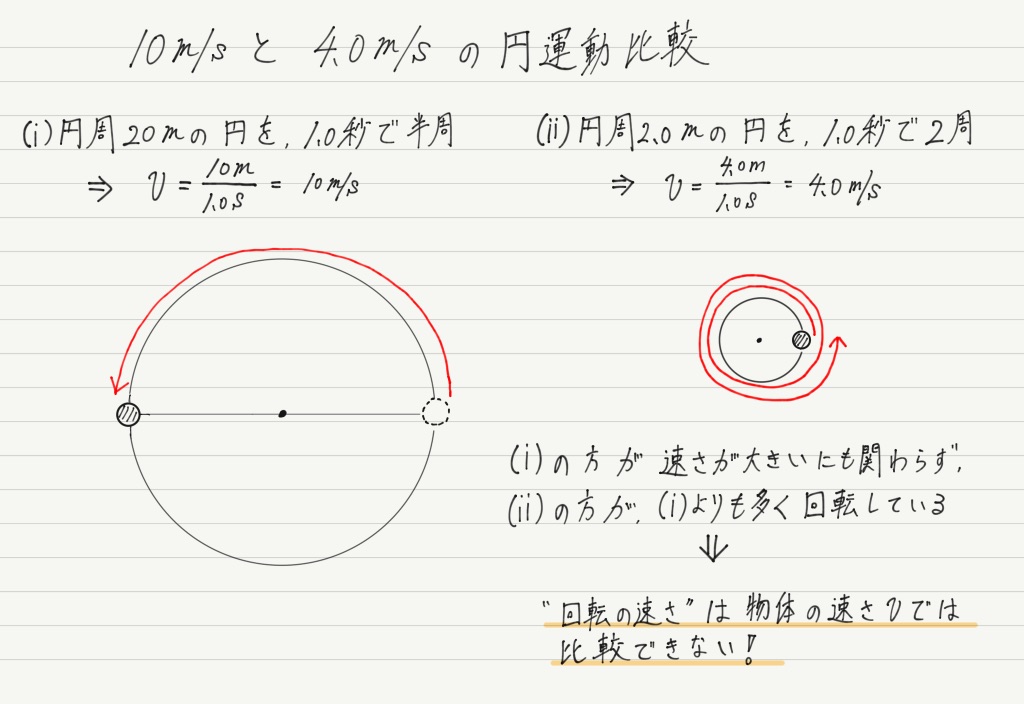
例えば,「1秒間に10m進むのと4.0m進むのとではどちらが速いか?」と言われたら,もちろん10mですよね?
いまこの問題を聞いたとき,みなさんは無意識に直線運動をイメージしませんでしたか?
円運動だとどうなるか,ちょっと見てください。
そりゃ10m/sと4.0m/sを比べたら10m/sの方が速いですが,円運動として見た場合,「どれだけの距離を進んだか」よりも,「何周まわったか」を基準に速さを考えたほうが適切な場合もあります。
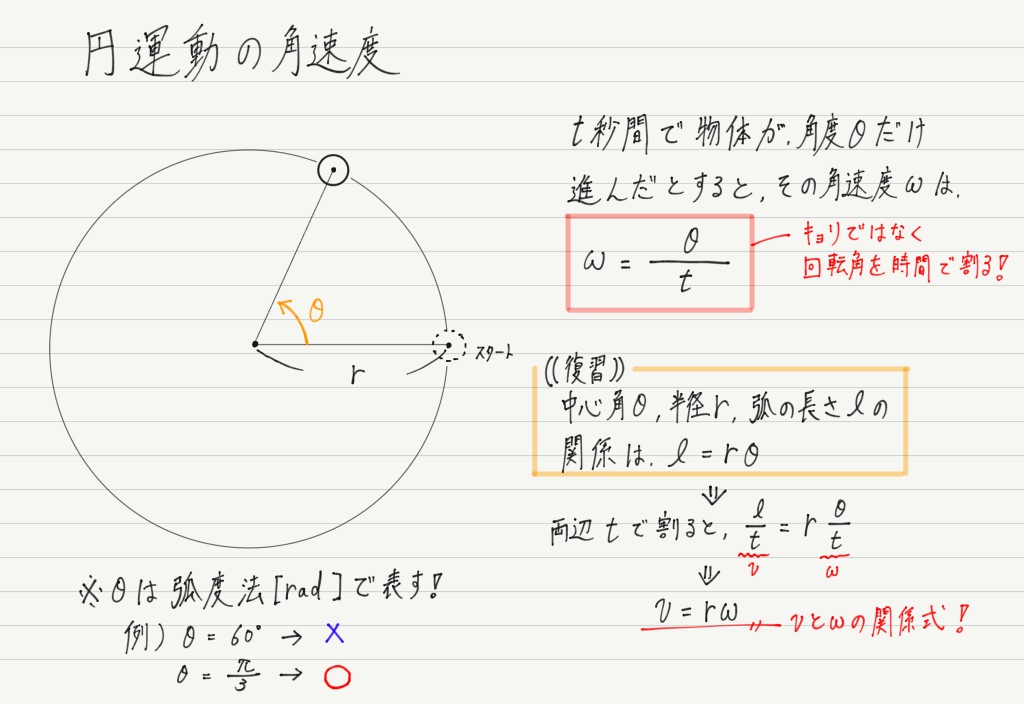
これを表すのが角速度です。
角速度の記号ωは,(´・ω・`)などの顔文字で目にしたことがあると思います。 読み方は「オメガ」。
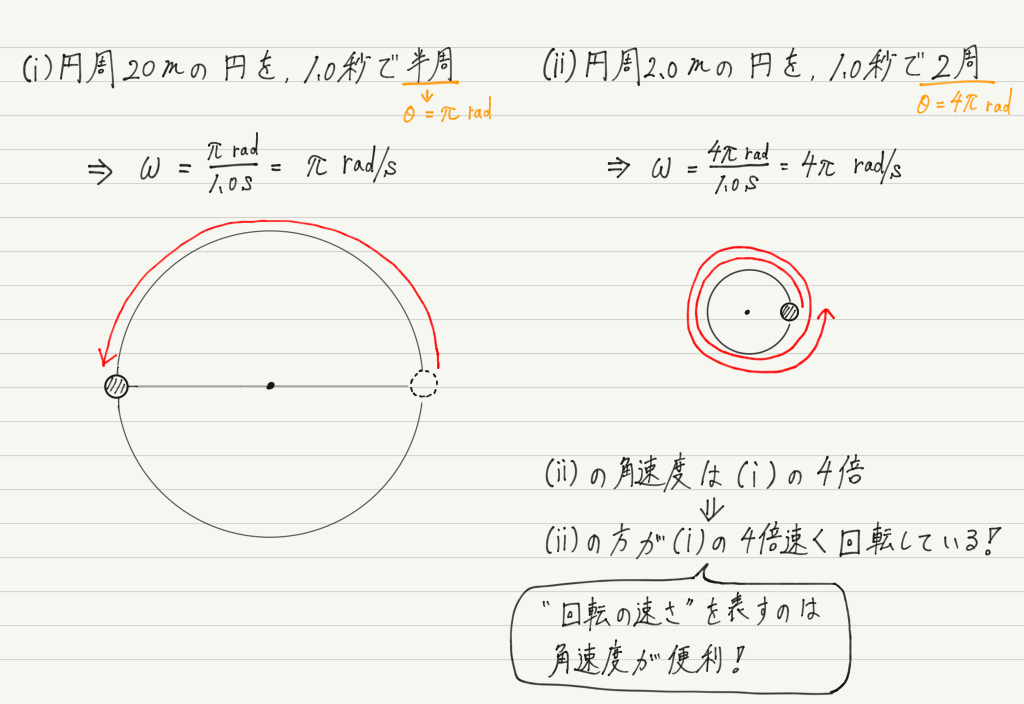
角速度ωを用いて,先ほどの例をもう一度考えてみると…
角速度のほうが優れているというわけではなく,円運動では速度と角速度を適切に使い分けることが重要。
ちがいをしっかり認識してください。
周期と回転数
物体が等速で円運動する場合,1周して元の位置に戻ってくるまでの時間を周期,1秒間に回転する回数を回転数といいます。
名前がちょっとちがいますが,これは波の分野で学習した周期と振動数の関係とまったく同じ。
うーん,簡単。 ついでにさっきの速度や角速度との関係も調べておきましょう。
円運動の分野,ご覧のとおり出てくる式はちょっと多め。
丸暗記するのではなく,自力で導出できるように練習しておくと理解が深まると思います。
今回のまとめノート
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。
次回予告
慣性の法則によれば,力がはたらかなければ物体は等速直線運動をするはずなので,円運動する物体は何らかの力を受けていることになります。
次回はこの力について考えていきましょう。