運動量保存則で「衝突」というキーワードが出てきましたが,せっかくなので衝突についてもう少し掘り下げてみましょう。
自由落下したボールが床と衝突するとき,野球のボールとテニスボールでははねかえる高さが異なります。
もっと極端な例を挙げれば,粘土を丸めてつくったボールだと床にくっついてしまってはねかえりません。
このように材質によってはねかえりやすさが異なるわけですが,今回はその「はねかえりやすさ」を表す方法を伝授したいと思います!
はねかえり係数の式
結論から言ってしまうと,「はねかえりやすさ」は,はねかえり係数(反発係数)と呼ばれる値で表すことができます。
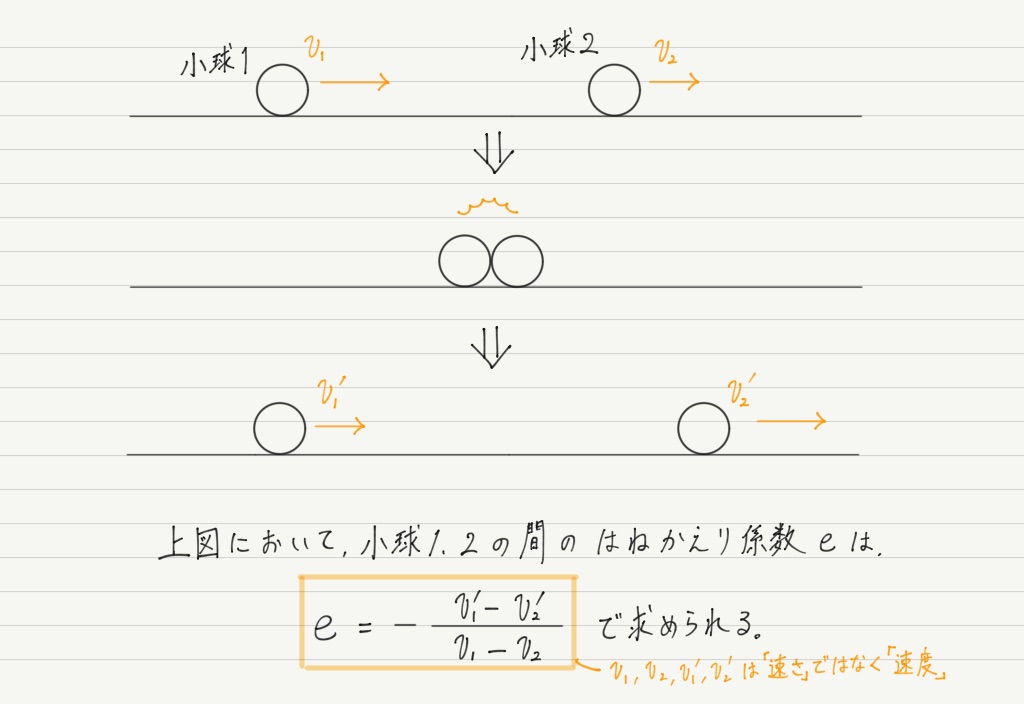
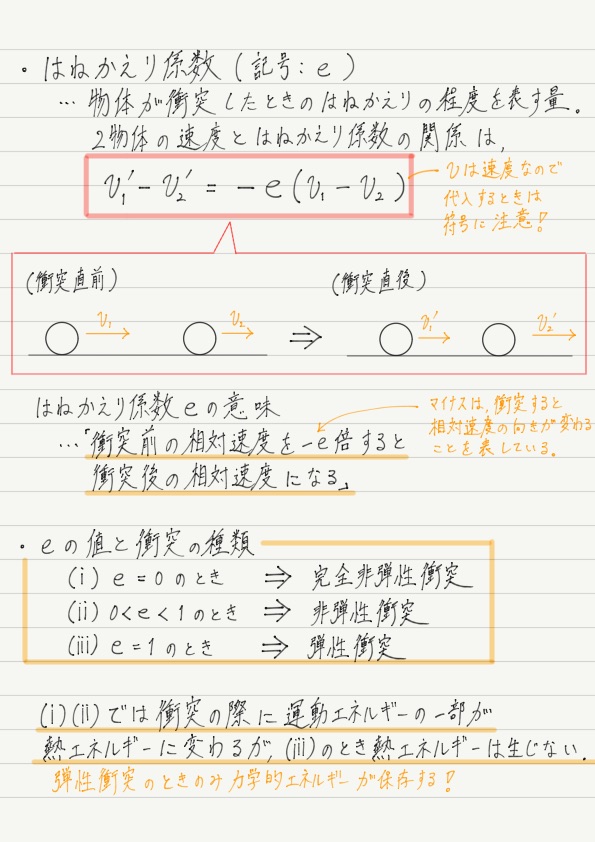
はねかえり係数は以下のような式で求められます。
イマイチわかりにくい!と評判のこの式ですが,ゆっくり見ていきましょう。
我々の目的は物体のはねかえりやすさの数値化です。
床との衝突なら,はねかえったときの高さを比べればはねかえりやすさを知ることができます。
しかし,物体の衝突先がいつも床とは限らないし,ビリヤードのように物体どうし水平に衝突することもあるので,「はねかえった高さを使って求める」という方法は万能ではなさそうです。
そこで,高さの代わりに目をつけたのが速度。
はねかえりやすい物体とそうでない物体とでは,はねかえった直後の速度がちがうというのがポイント(もちろんはねかえりやすい物体のほうが衝突後大きい速度をもつ)。
そして,速度なら水平に衝突する場合でも計算可能!
ところがこの式,ただ単に速度を使っているわけではなく,速度を引き算しています。
この引き算は何だかわかりますか??
速度から速度を引く… そう,これは相対速度に他なりません!!
(物理基礎の補講で扱った話題なので未読の方はまずはこちら↓をどうぞ。)
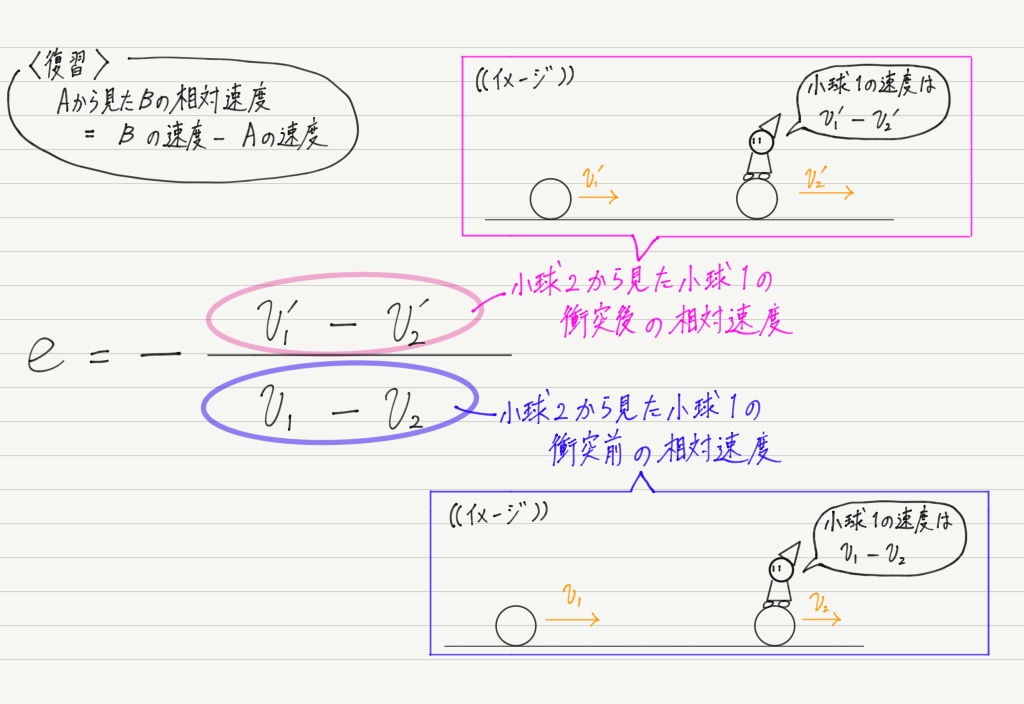
相対速度を念頭に置いた上で,もう一度式を見てみると,
動く物体が2つあるときに,片方を基準してもう片方の相対速度を考えるのは物理ではよくやる手段。
相対速度に苦手意識がある人はこの機会にしっかり復習しましょう。
それから公式丸暗記マンによく見られるのが,「どっちからどっちを引くんだっけ?」というもの。
どっちを基準にするかはその人の自由なので,引く順番はどっちでもいいです。
はねかえり係数の意味
ところで,はねかえり係数という名前に疑問を感じませんか?
はねかえり“定数”じゃなくて,はねかえり“係数”。
「y = axで,xの係数はa」のように,“係数” というからには何かに係っていないといけないはずなんだけど…?
というわけで,先ほどのはねかえり係数の式を式変形してみます!
実はこれがはねかえり係数の式の真の姿!!
はねかえり係数とは,衝突前の相対速度に係っている数。
こうすると,はねかえり係数の意味が一目瞭然。
「衝突した後の相対速度の大きさが,衝突前の相対速度の大きさの何倍になっているか」を表しているのがはねかえり係数です!
教科書に書いてある分数の形は丸暗記しようとして分母分子を間違える人が後を絶ちません。
こちらの分母をはらった形で覚えることをオススメします。式の意味もわかりやすいし。
(計算するときはどうせ分母をはらうことになるんだから,だったら最初から分母はらっておいたほうがいいっていう理由もあります。)
衝突の種類
はねかえり係数は衝突する物体の材質によって変化しますが,必ず0以上1以下の値にしかなりません。
もしはねかえり係数が1より大きかったら衝突後の相対速度が衝突前より速くなることになりますが,エネルギーの観点から考えると「衝突しただけで運動エネルギーが増えた」ことになってしまって,明らかにおかしいです(そんなことができたら世の中のエネルギー問題は即座に解決!笑)。
物体系の外から仕事をされない限り,運動エネルギーが増えることはないので,はねかえり係数は最大で1であることがわかります。
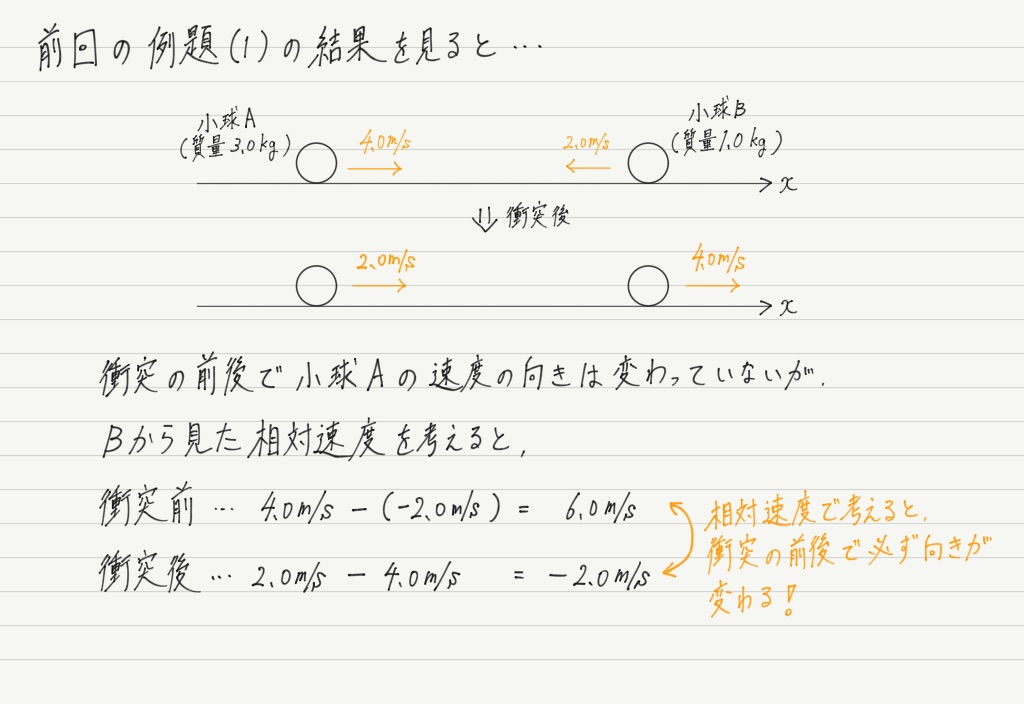
また,衝突の前後で相対速度の向きは必ず変化するので,はねかえり係数がマイナスの値になることもありません。
以上より,はねかえり係数eの範囲は,0 ≦ e ≦ 1であることがわかります。
衝突はeの値に応じて3種類に区別されており,それぞれに名前がついているのでぜひ覚えてください。
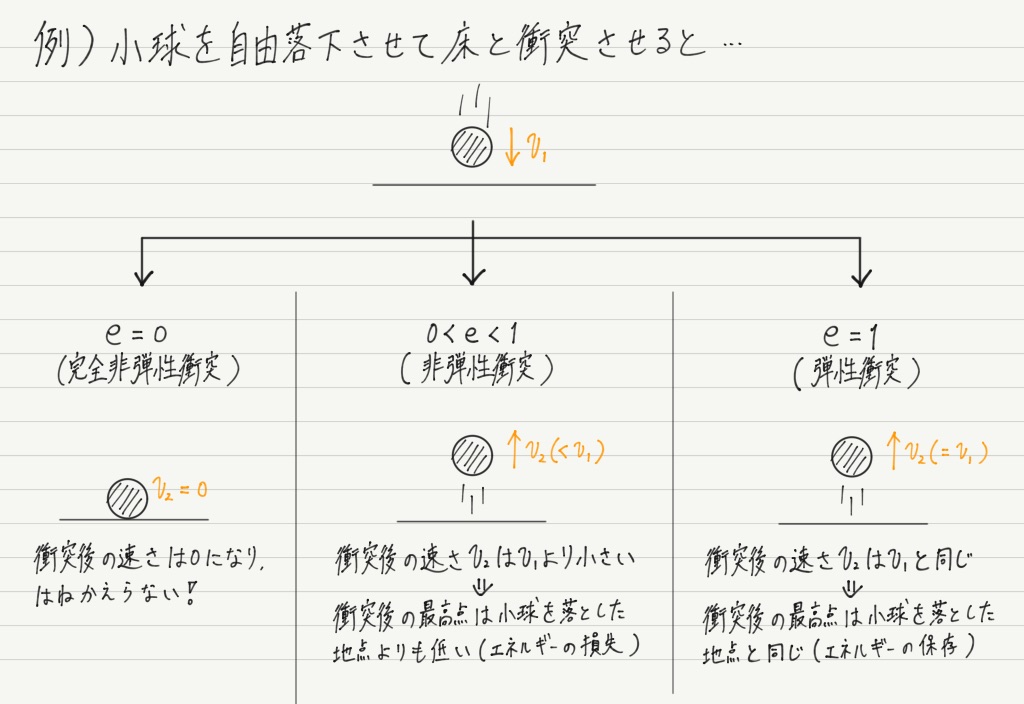
e = 0 → 完全非弾性衝突
0 < e < 1→ 非弾性衝突
e = 1 → (完全)弾性衝突
通常の物体の衝突は非弾性衝突,粘土を床に落としたときのように物体がはねかえらないのが完全非弾性衝突です。
ここでもう一度エネルギーの話を持ち出すと,0 ≦ e < 1の衝突では衝突の前後で相対速度が小さくなるので運動エネルギーが減少する(減少した分は熱エネルギーとして大気中に逃げる)ことになります。
衝突の問題で力学的エネルギー保存の法則が使えない問題が多いのはこのせいです。
一方,弾性衝突は,衝突の前後で相対速度が変わらない(=力学的エネルギーが保存される)理想的な衝突です。
衝突の問題ではどの衝突が起こるのか,条件を見逃さないよう心がけましょう。
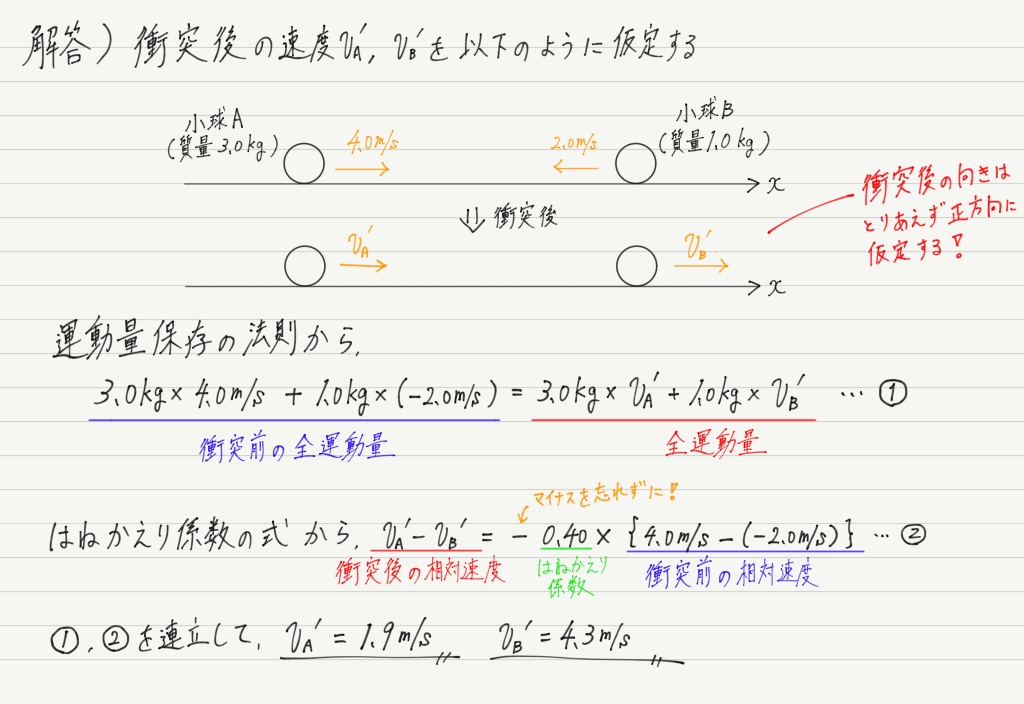
例題
最後に,はねかえり係数の式を使う基本問題を紹介します。
はねかえり係数の式を使うといっても,それだけでは解けませんよ??
解答はこの下にあるので,解き終わったらスクロールして確認してください。
解答です!
はねかえり係数が登場するのは衝突の問題。 そして衝突の問題の主役は何といっても運動量保存則。
この例題のように,はねかえり係数の式と運動量保存則は組み合わせて使うことが圧倒的に多いので,問題演習を通じて慣れておきましょうね!
今回のまとめノート
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。
次回予告
運動量関連の話はこれにて終了。 次回からは直線運動でも放物運動でもない,新たな運動にチャレンジしましょう!