授業で先生が「ここ重要だよー」とかよく言いますが,ぶっちゃけ力学は全部重要です笑
しかし重要の中にも序列があって,今回学習する運動量保存の法則は運動方程式や力学的エネルギー保存の法則と並ぶ最重要法則です。
前回の運動量と力積の関係がベースになるので,よく復習した上で先に進んでください。
2物体の衝突
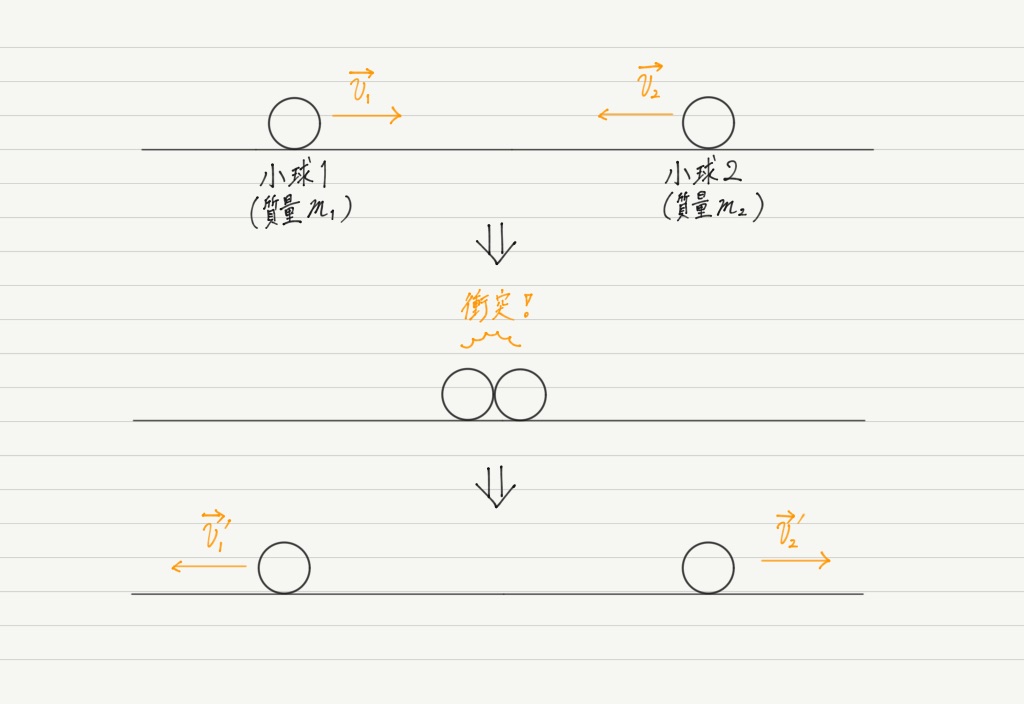
以下の図のように, 直線上で小球が衝突する現象を考えましょう。
衝突によって2つの小球が力を及ぼしあっている時間はごくわずかなので,運動量と力積の関係を用いることができます。
いま小球1について式を立てましたが,小球2についても同様に運動量と力積の関係式を立てることができるはずです。
2つの式をそれぞれ足して,式変形してみると…
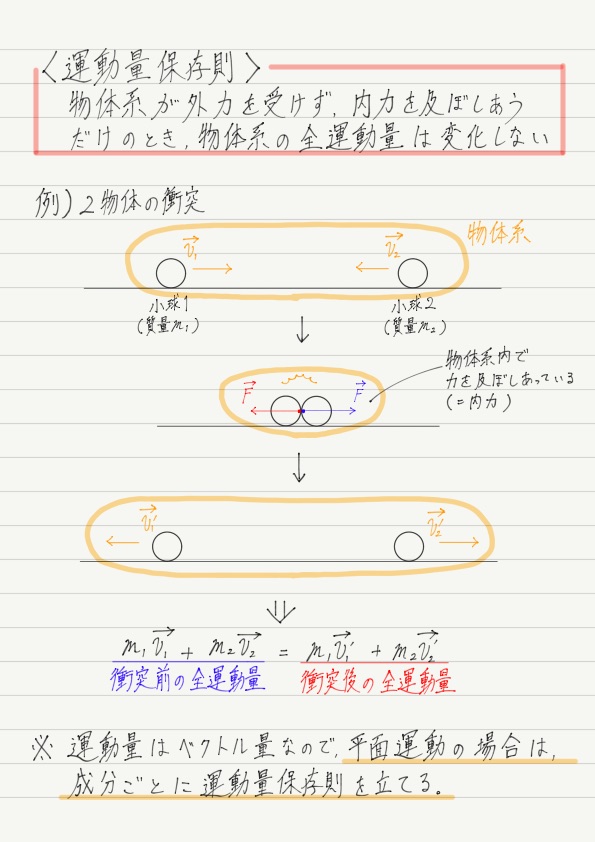
この式は,衝突する前と衝突した後で,2つの小球の運動量を合計したものは変化しないことを示しています。
これが「運動量保存の法則」です!
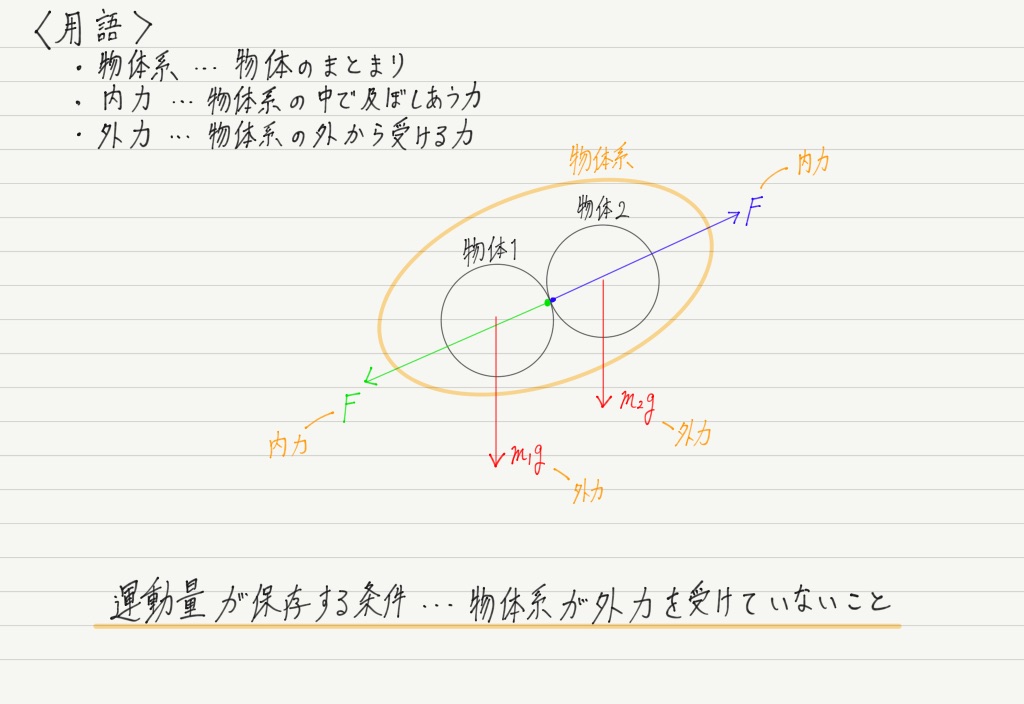
運動量が保存する条件
このように,物体が衝突する問題では運動量保存則が大活躍します。
が,せっかくの強力な法則なので,もうちょっと欲張ってみましょう。
つまり「衝突以外にも運動量が保存する場面はあるか?」という問題です。
この問題を言い換えると,「運動量はいつ保存するのか」ということになりますが,もう一度さっきの計算に注目してください。
運動量保存則を導くときの最大のポイントは連立して力積が消えるところ。
そして,力積が都合よく消えてくれる理由が作用反作用の法則であることは,上の計算を見ればわかります。
よって,運動量保存の法則が成り立つ条件は,「物体どうしで力(作用と反作用)を及ぼし合っているとき」と結論づけることができます!
(※ さっきの小球どうしの衝突では重力と垂直抗力が外力としてはたらいていますが,この2つはつりあっていて合力0のため,運動量の変化には影響を与えません。)
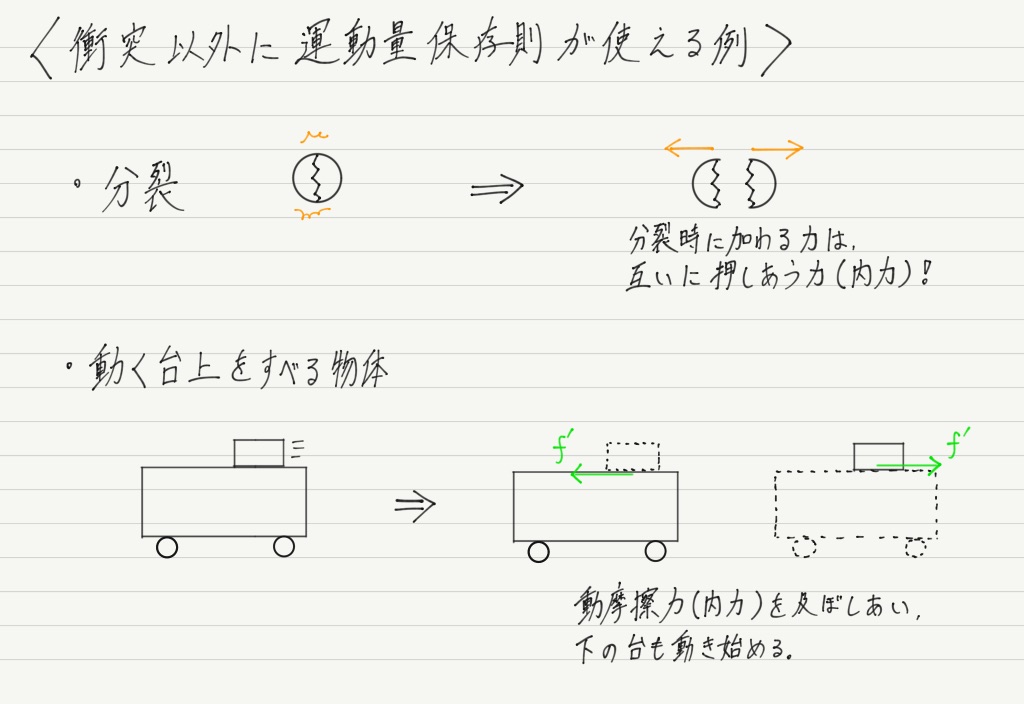
及ぼしあっているのが内力だけならば,衝突以外でも運動量は保存します。
問題でよく見かけるのは「分裂」と「動く台上で動摩擦力を受けてすべる物体」かなぁ。
例題
超大事な法則なので,簡単な例題ぐらいはやっておきましょう。
まずはがんばって解いてみて!
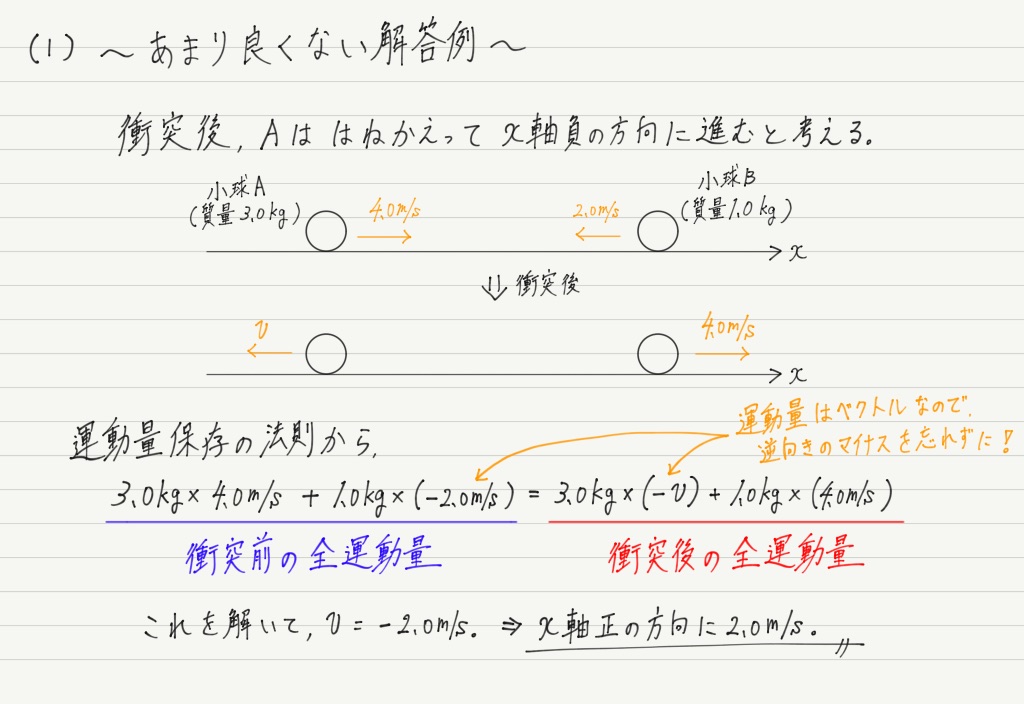
では解説。 まずはあまり良くない解答例をご覧ください。
運動量保存則を使う問題で一番多いのが,この例題のような衝突後や分裂後の物体の速度を問う問題ですが,この手の問題で計算間違いを減らすコツがあります。
それは,「衝突後(分裂後)の速度の向きを深く考えない」ことです。
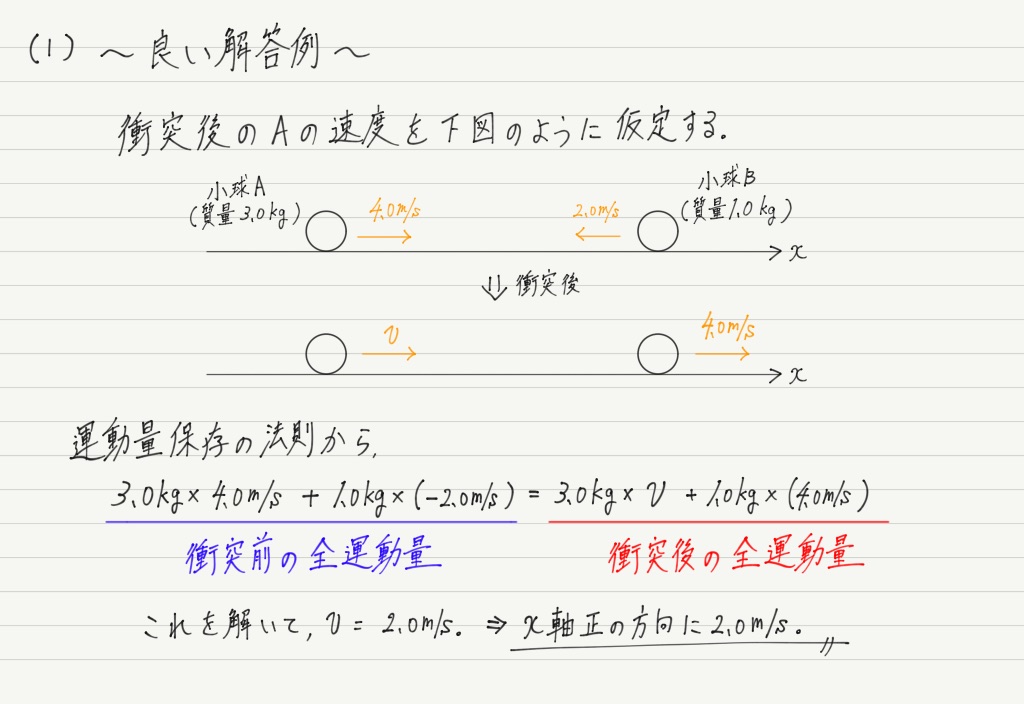
良い解答例を見てもらったほうが早いですね。
良くない解答例と良い解答例,そんなに差があるようには見えませんが,良くない解答例はミスしやすいポイントをいくつか含んでいます。
あまり良くない解答例のどこが良くなかったか,もう一度見てみましょう。
このように,最初に衝突後の向きを考慮しようとすると,
① 向きを考えるのに時間がかかる。
② 式を立てる段階で余計なマイナスが出てきてしまって,計算ミスしやすい。
③ 実際計算してみたら,せっかく時間をかけて考えた向きが間違っていたりする。
と,いいことがひとつもありません!
向きは頭で考えてもどうせ分からないんだから,良い解答例のように「わかんないけどとりあえずx軸の正方向だと仮定しておくかー」という態度で臨むのが賢明。
時間も節約できるし,計算ミスも減ります。
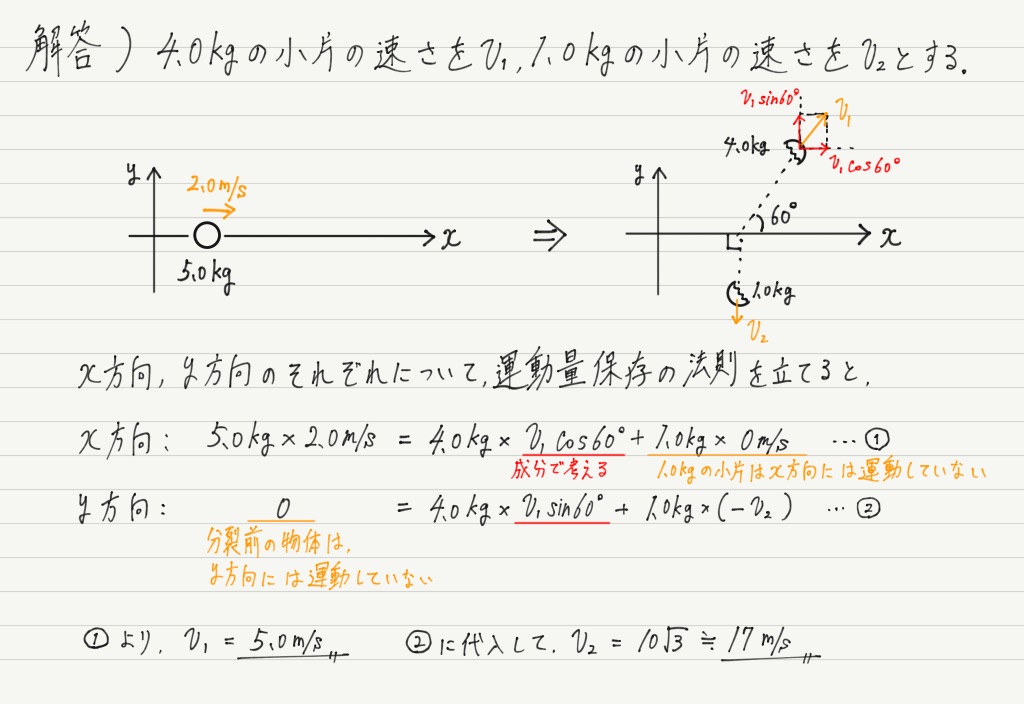
では(2)の解答も見てみましょう。
(2)は平面運動なので,斜方投射などと同様にx軸方向とy軸方向に分けて考える必要があります。
斜めの速度は成分分解して使いましょう!
運動量保存の法則は基本問題からハイレベルな問題まで,ありとあらゆるところに顔を出します。
いろんな問題を解いて,徐々に慣れていってください!
今回のまとめノート
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。
次回予告
衝突問題で,運動量保存の法則とセットで登場することが多い「はねかえり係数」を扱っていきます。