物理基礎の力学のメインは質点の運動の様子を調べることでした。
運動を調べるための基本的な道具は運動方程式ですが,運動方程式をやる前に力についての話がだいぶ長く続きましたよね。
アレにはうんざりした人も多いかと思います。
とはいえ,運動の原因は力なので,それを無視して話を進めることは不可能なわけです。
さて,剛体の力学のメインは「回転」なのですが,これも本題に入る前に原因究明を先にやっておきましょう。
力の大きさで回転は決まらない
質点の運動は,はたらく力の向きと大きさで運動が決まりました。
力が大きいほど加速度が大きくなる,という具合です。
回転運動はどうでしょう? 何かを回転させるとき,やはり力の大きさが関係しているように思えます。
それはもちろん間違っていないのですが,回転はそれほど単純ではありません。
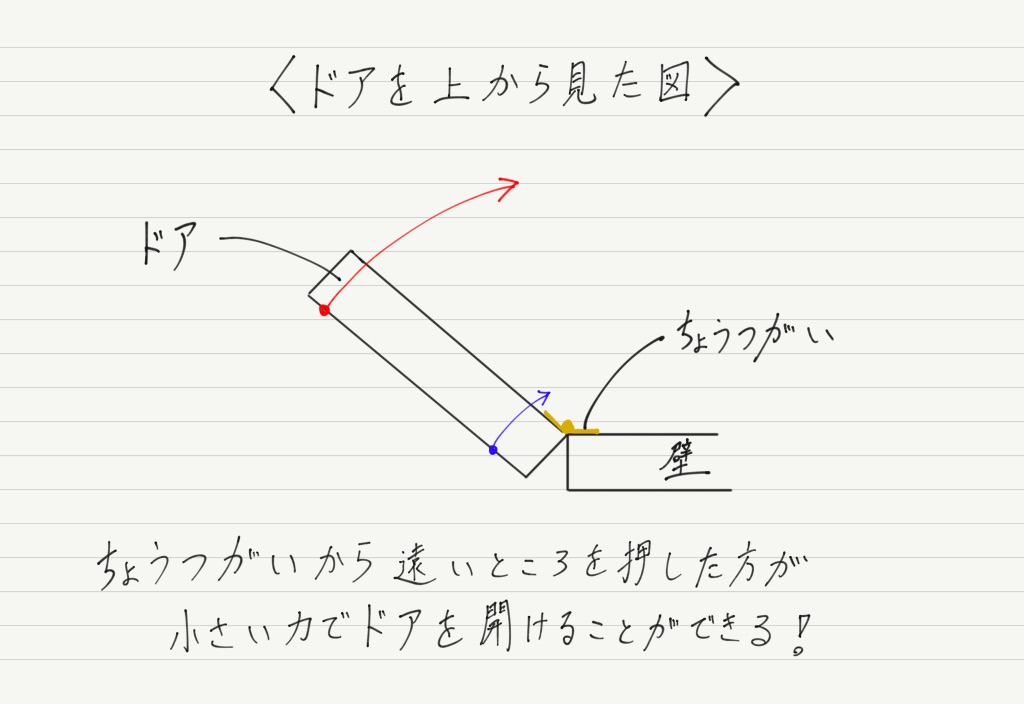
ドアを例にとりましょう。 ドアは蝶番(ちょうつがい)を中心に回転することで開閉します。
ドアを押して開けることを思い浮かべてください。
あなたならドアのどの部分を押しますか?
…そりゃドアノブのところですよね!
仮にドアノブがなかったとしても,あなたは「ドアノブがあるべきはずのところ」を押して開けるはずです。
ドアノブのあるべきところ,それは蝶番からもっとも遠いところ!!
もし蝶番のすぐ近くを押したとすると,同じ力ではドアは開かないはず。
同じ力を加えても,押す場所によって回転のしかたが違うということは,回転が力の大きさだけでは決まらないことの決定的な証拠です!
回転の原因は「力のモーメント」
もう気づいたと思いますが,物体を回転させるには力の大きさの他に「回転軸(回転の中心)からの距離」が大きく関係しています。
ドアの場合,蝶番から遠いところだと小さな力でもドアを開けられますが,蝶番の近くだと大きな力を加えないと開けられません。
あれ? これってどこかで聞いたような??
そうです! てこの支点と力点の関係と同じですよね!!
小学校のときにてこの分野で習ったことは,実はてこに限らず,すべての回転について成り立つのです!
話をドアに戻しましょう。 いま分かっていることは,
・同じ力で押すなら,中心から遠いほうが回しやすい。
・同じ場所を押すなら,大きい力のほうが回しやすい。
ということ。
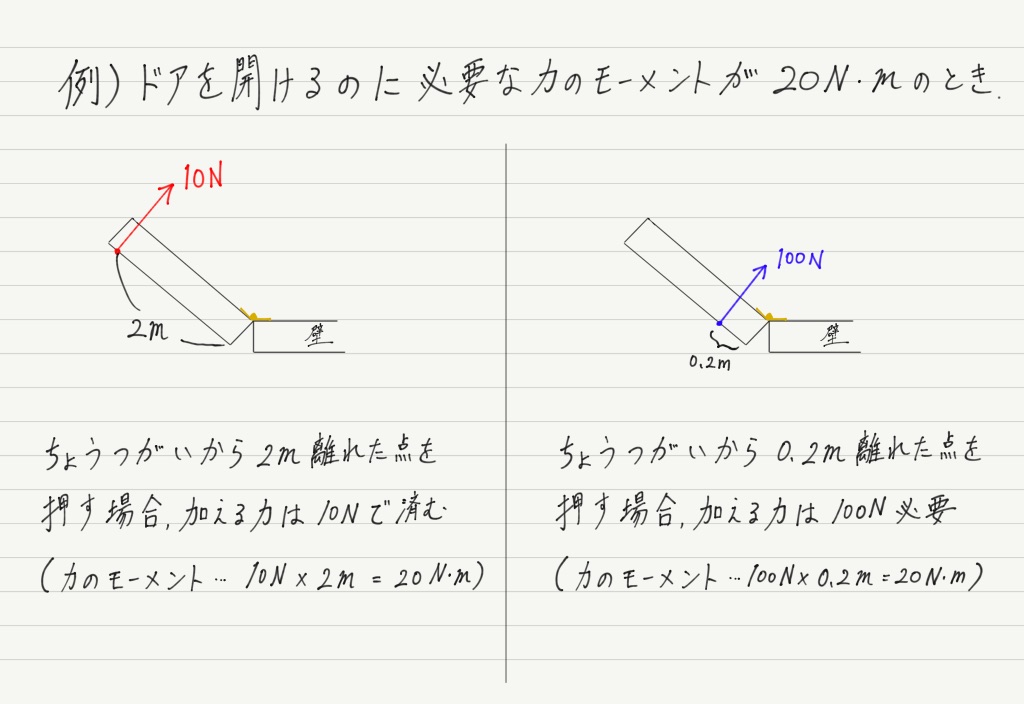
結論を言うと,ある点Oを中心に物体を回転させるはたらきは「力の大きさ × 点Oからの距離」で決まり,これを「力のモーメント(単位:N・m)」といいます。
蝶番から遠いところを押すと小さな力でもドアが開くのはこれで説明できますね!
「中心からの距離」をどう測るか
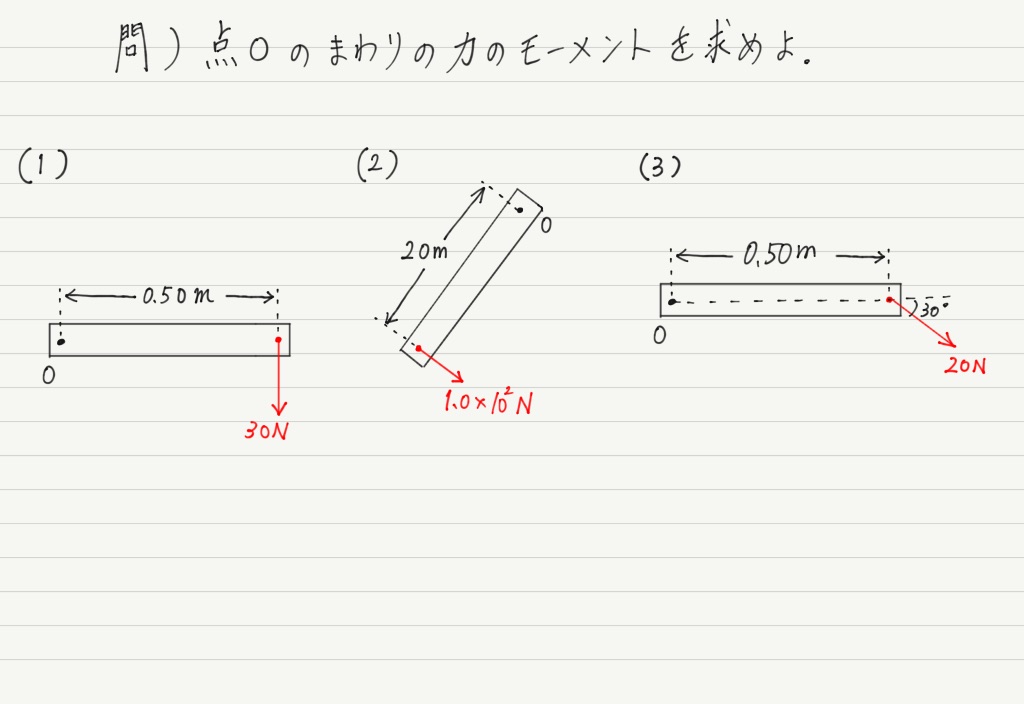
では力のモーメントを計算してみましょう。
上のドアの例では力のモーメントの大きさのみを計算しましたが,力のモーメントは「向き」も大事。
力のモーメントの向きは,点Oを中心に物体を「時計まわり」に回転させるのか,「反時計まわり」に回転させるのかの2択です。
向きにも気をつけて例題をやってみてください。
答えはこの下にあります。
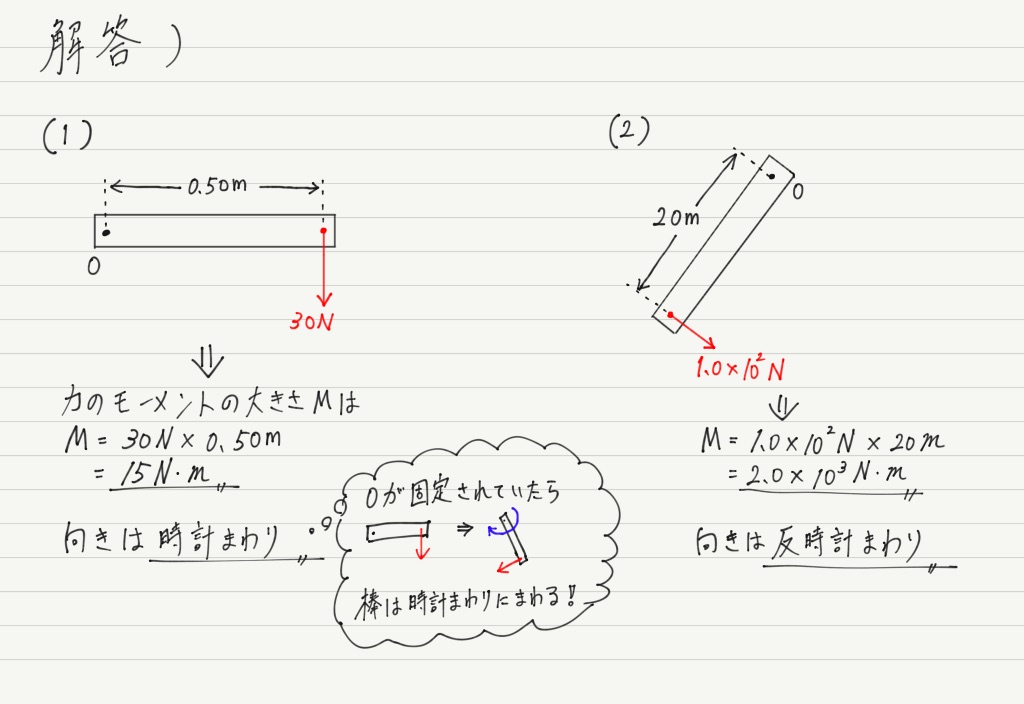
できましたか? それでは解答です。
後に(3)ですが,答えは10N・m
…ではありません!! これは初学者が間違えやすい問題なので要注意。
力のモーメントの計算で唯一注意しなければいけないこと。 それは,「点Oから力までの距離の測り方」です。
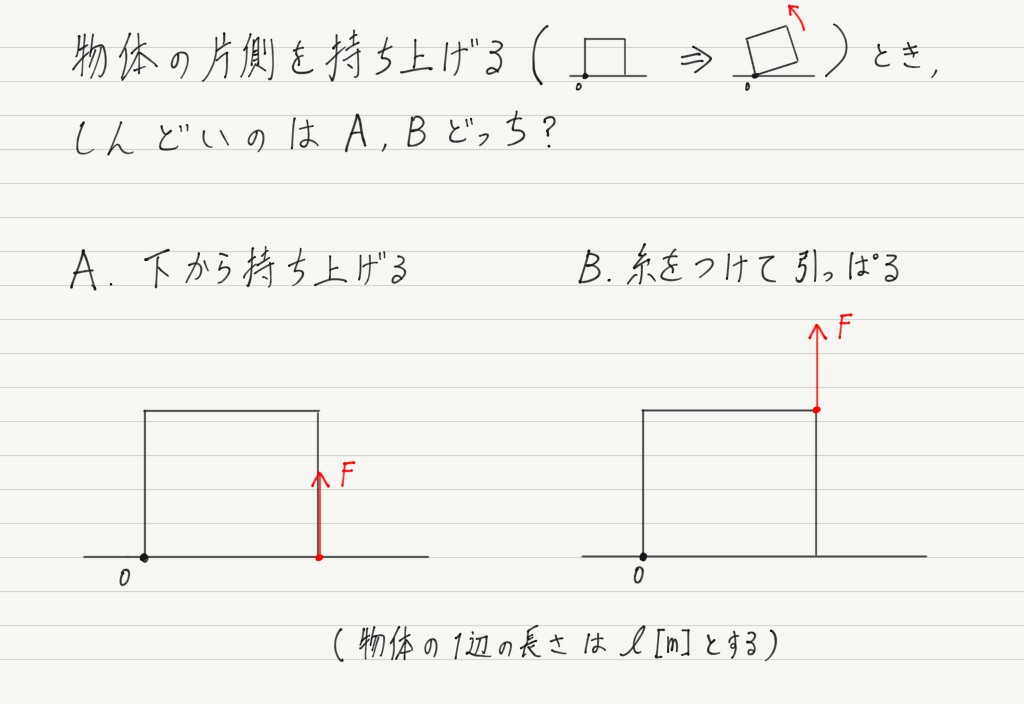
(3)の解答はいったん後回しにして,別の問題を考えてみましょう。
結論を言ってしまうと,「どっちもしんどさ(=持ち上げるのに必要な力のモーメント)は同じ」です。
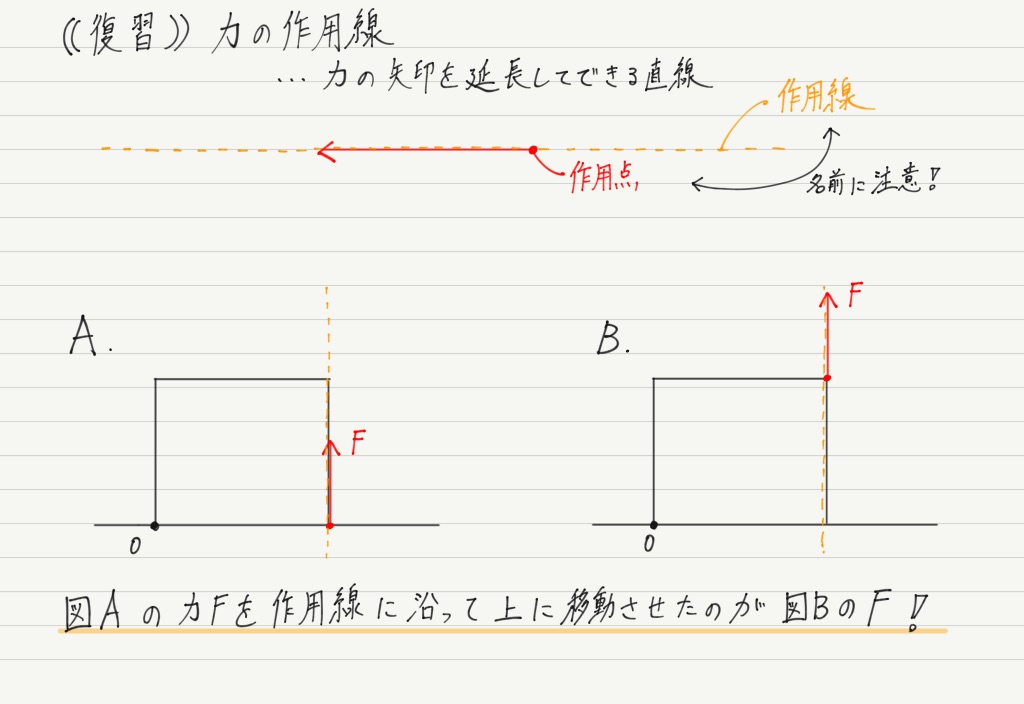
実は力のモーメントを求めるとき,「力を作用線上で移動させても力のモーメントは変わらない」ことが知られています!
よって,上の図のAとBは同じ力のモーメントをもっています。
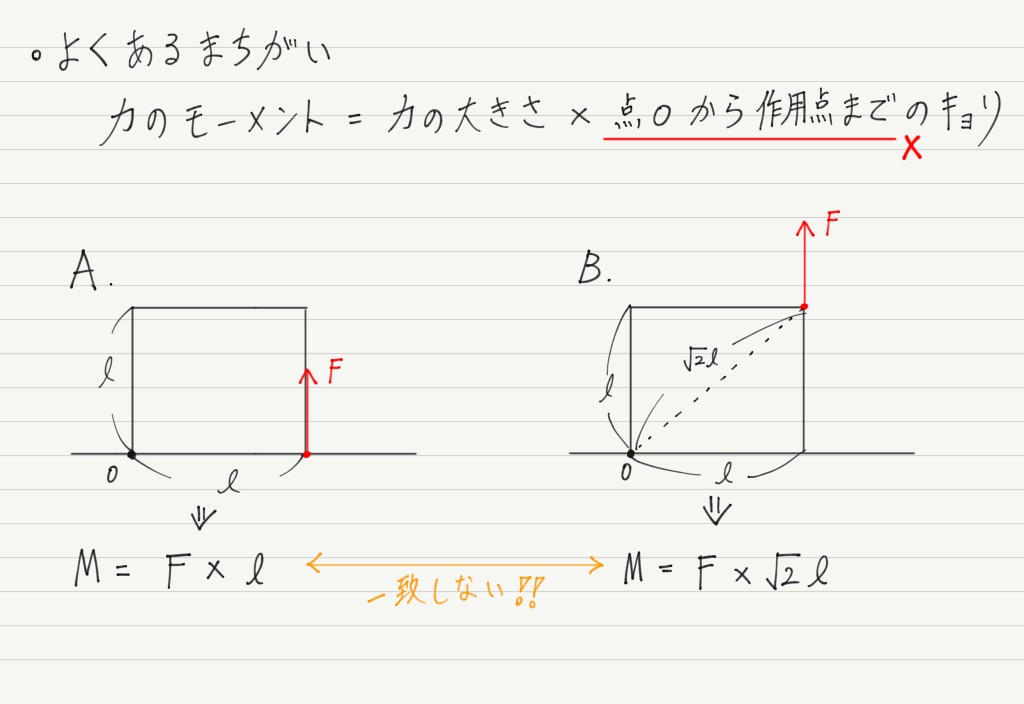
ところが力のモーメントを求めるとき,「点Oから力の作用 “点” までの距離」を使って計算すると,AとBのモーメントが異なる値になってしまってあれれ??
ではどうしたらいいか。
「作用線上を移動させてもはたらきが変わらない」ということから,力の作用点よりも作用線の方が大事ということが分かります。
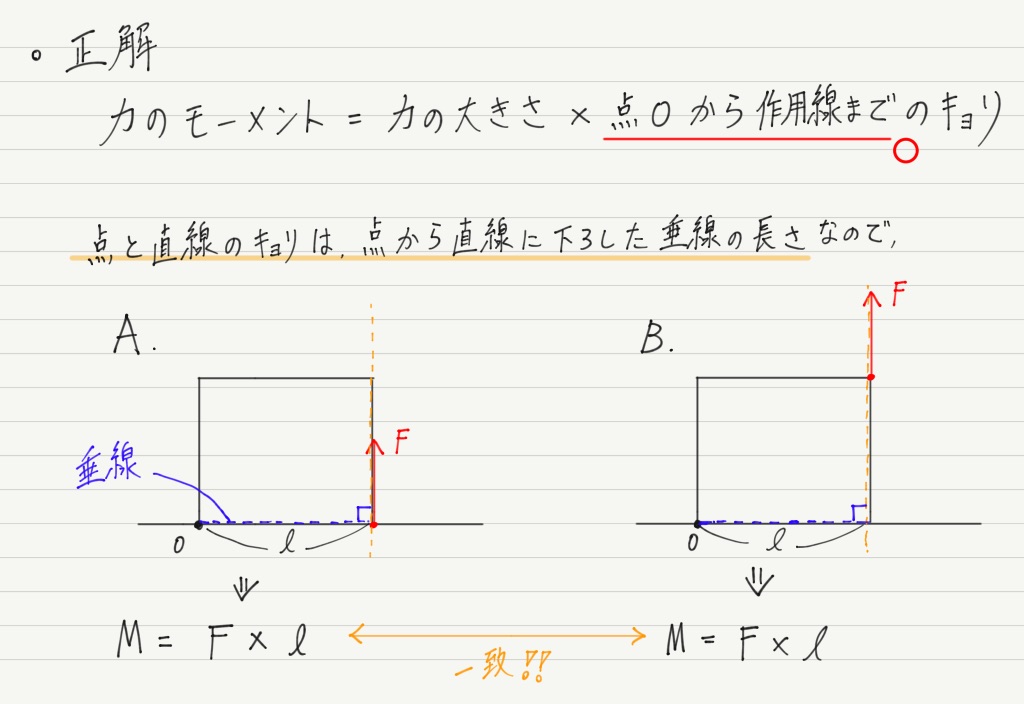
つまり,力のモーメントの計算では,「点Oから力の作用 “線” までの距離」を測るのが正解です!
これを踏まえると,最初の例題の(3)の解答はこうなります ↓
今回のまとめノート
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。
次回予告
回転の原因である力のモーメントが計算できるようになったので,次はいよいよ回転運動?