物理基礎の力学も終わり,いよいよ物理の力学に突入します!!
基礎で習った内容を土台に話を展開していくので,不安のある人はもう一度物理基礎を復習しておくこと。
物理基礎はだいたいOK!という人はこの先へGO!!
「物理基礎の力学」と「物理の力学」最大のちがいとは
比較的簡単なもの→物理基礎
やや難しい内容→物理
だと思っている人が多いですが,それはまちがい!!
実はもっと明確な分類がされています。 これを知った上で学ぶのと,ただ教えられたものをやるのとでは理解がちがってくるので,まずはそのちがいを教えておきましょう。
それはズバリ,「直線運動か平面運動か」です!
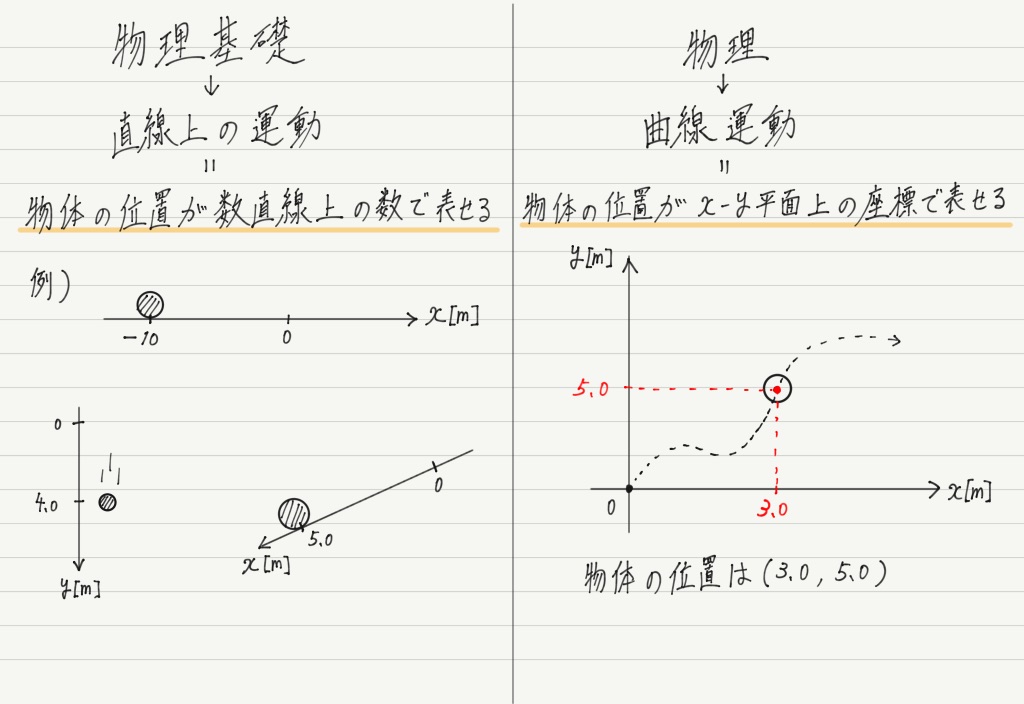
物理基礎で扱った運動は,等速直線運動と等加速度運動でした。 等速直線運動は名前のとおり「直線上の」運動だし,等加速度運動も自由落下や投げ上げなど,やはり扱ったのは「直線上の」運動です。
それに対して,物理の力学では曲線を描く運動を主に扱います。 直線運動は数直線上の運動としてで表現できますが,曲線運動だと座標平面を持ち出す必要があります。
このように平面を動き回る運動をこれから扱うわけですが,うまく扱うにはどうしたらいいでしょうか?
「ベクトル」という最強のアイテム
平面運動の扱いを簡単にしてくれるのが「ベクトル」です!!
「ベクトルなら物理基礎でもやったじゃん!」って? 確かに物理基礎でも速度や力を表す手段としてベクトルは登場していました。
「大きさ」と「向き」をあわせ持つ量で,矢印で表す。 問題ないですね?
しかし上でも述べたとおり,物理基礎の運動は数直線上の運動なので,「向き」とは言っても,右 or 左,上 or 下,斜面に沿って上 or 下,…結局,2択しかありませんでした。
2択ならプラスマイナスの記号だけで表せるので,ベクトルを詳しく知らなくても特に問題なかったわけですが,平面上の運動を扱う場合はそうもいきません。 数学Bで習うベクトルの基礎(和,差,成分表示,大きさなど)は使いこなせるように確実にマスターする必要があります!!
ここで数学の話をしだすとキリがないので割愛しますが,詳しく知りたい方はこちらの記事を読んでください。
物理基礎で習った概念をベクトルで書き直してみる
「直線運動から平面運動になり,ベクトルを用いて運動を表す」と聞くといかにも難しそうに思えますが,めちゃくちゃ簡単です。
まず,新しく覚え直す公式は1つもありません。 運動に関する基本的な式として,変位の式,速度の定義式,加速度の定義式,相対速度が挙げられますが,まずは物理基礎ver. を見てください。
これを物理ver. にするとこうなります。
文字の上に記号「→」を追加してベクトルにしただけ!笑
しかし見た目の変更はわずかでも,計算方法は大きく変わります。
ベクトル量の計算
物理に出てくるベクトル量の代表格は力。
ベクトルの計算の注意点は,以前力の合成のところで一度説明しています。
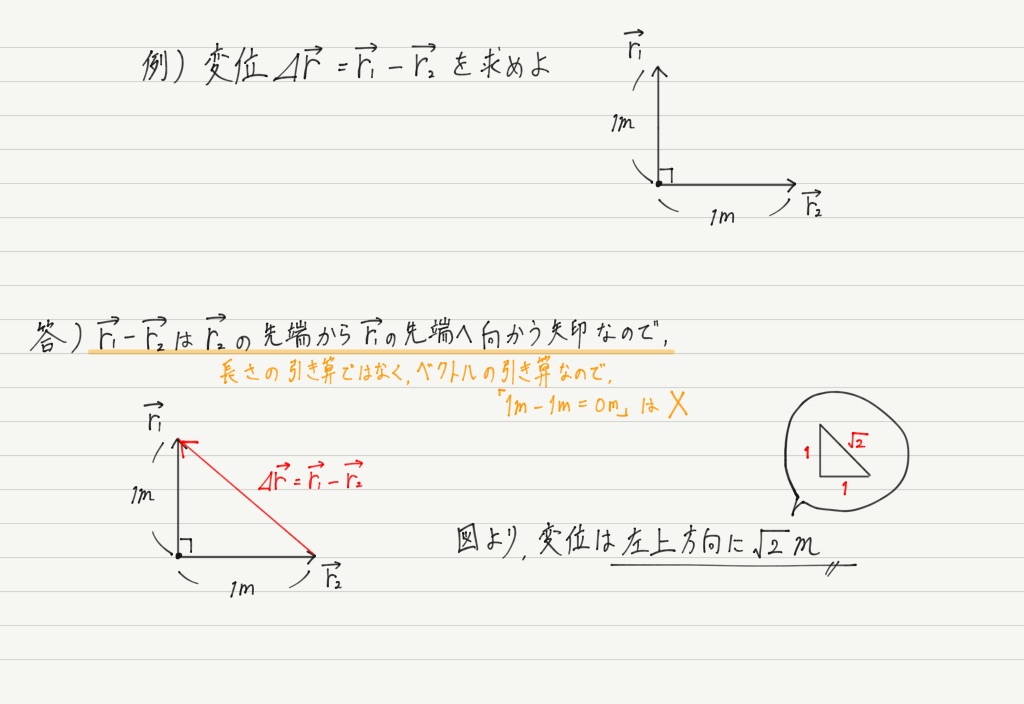
一言で言うと,「1Nの力と1Nの力を足しても2Nになるとは限らない」ということです!
これは力に限った話ではなく,ベクトル全般について共通して言えることです。
つまり,「ただ数字を足したり引いたりするのではなく,向きを考慮する」ことが重要になります。
一番よく使うのは成分表示
とはいうものの,いま例題で見たような,ベクトルの「図形的な計算」は正直作図の問題でしか使いません。
物理で「ベクトルの計算」と言った場合,ほとんどは「成分に分けて,成分ごとに計算」を意味しています!!
平面運動はx成分とy成分の2つに分けることができますが,成分ごとにそれぞれ計算すれば,それでベクトルの計算は完了です!
成分ごとに計算すると手間が2倍になりますが,成分に分けてしまえば先ほどのような「図形的な計算」ではなく「数値の計算」になるので,むしろ簡単です。
先ほど速度と加速度の定義もベクトル表記で書きましたが,実際に用いる場合には,
このように成分に分けて,それぞれでいつもどおり速度と加速度を求めてあげればよいのです。
平面といえば座標,速度や加速度といえばベクトルですが,いま見たとおり,ベクトルは成分表示することで座標とみなせます。 これで座標とベクトルの話がつながりましたね!
例題
簡単な問題を問いて感覚をつかんでください。
解き終えたらスクロールして,答え合わせしてください。
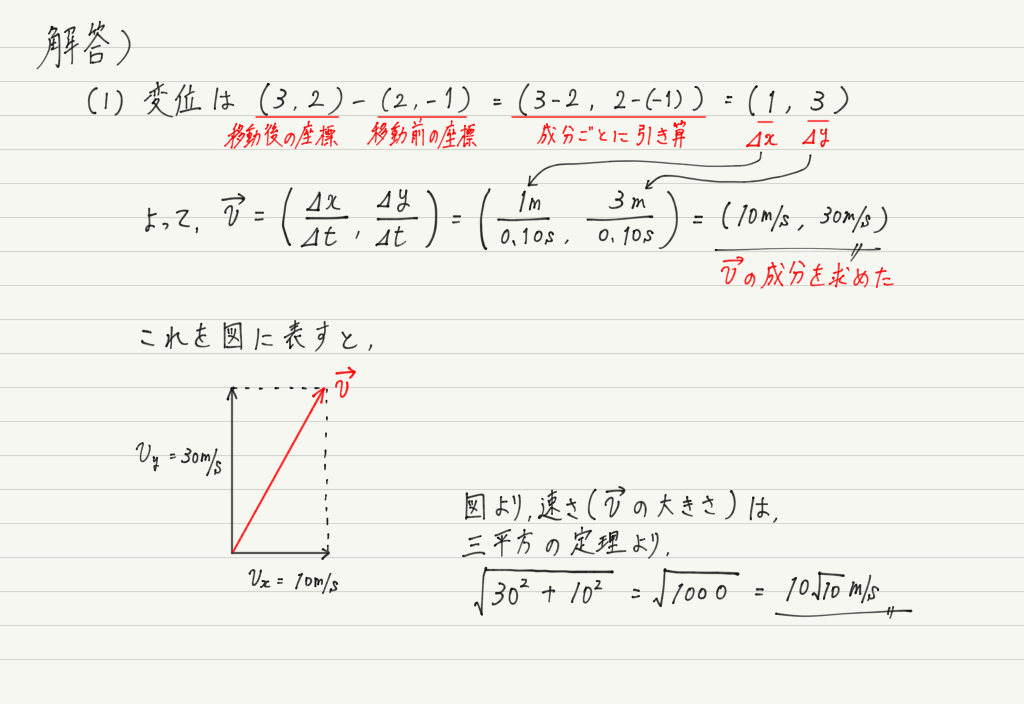
では解答です!
平面運動ではこのように,成分ごとに計算することを心がけましょう!
今回のまとめノート
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。
次回予告
今回は概念的な話だったので,よくわからなかったという人もいるかもしれません(ベクトルが苦手 or 未習の人は特に)。 普段なら「わかるまで復習して!」と言いたいところですが,今回はあまり気にせず先に進んで構いません。
次回は具体的な運動を扱っていくので,平面運動へのアプローチの仕方がより実感できると思います。