位置エネルギーと聞くと,前回学習した「高いところにある物体がもつエネルギー」を真っ先に思い浮かべると思います。
しかし実は位置エネルギーというのはもっと広い意味で使われる用語で,高いところにある物体の位置エネルギーはその中のひとつに過ぎません。 前回のタイトルにわざわざ “重力による”をつけたのもそのためです。
今回は別の位置エネルギーについて勉強しましょう。
ばねがする仕事
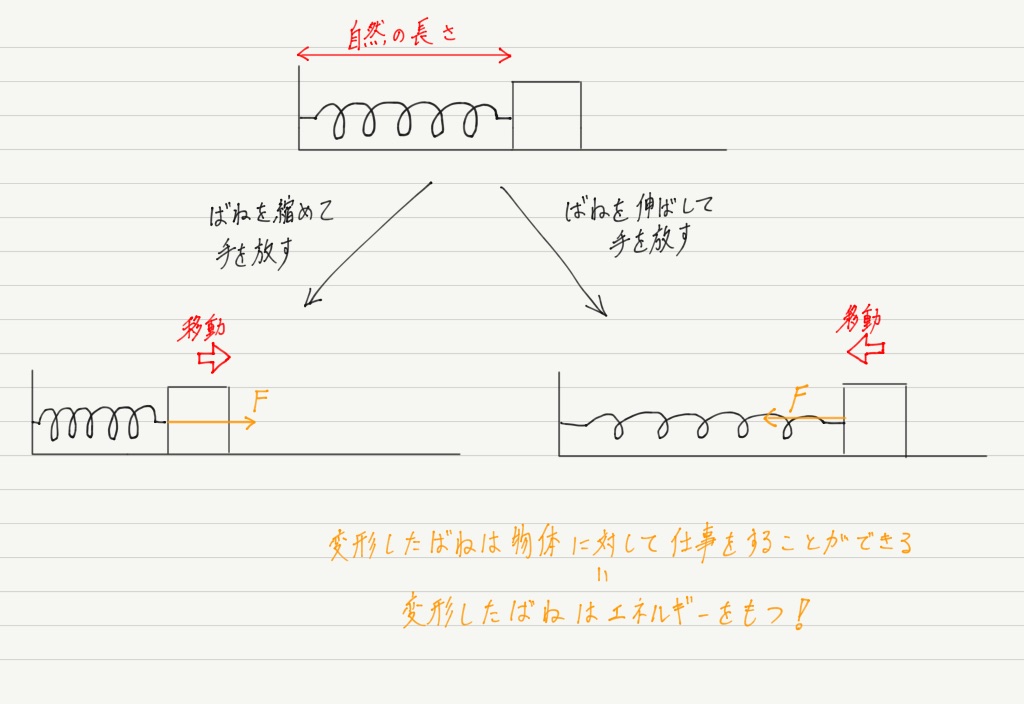
ばねは変形させると元に戻ろうとする力がはたらくので,その力で物体に仕事をすることができます。
仕事ができるということは,変形したばねはエネルギーをもっているということになります!
当然ですが,ばねが変形していなければエネルギーは0です(ばねの自然の長さのときがエネルギーの基準になる)。
変形していない状態から少しでもばねを変形させると,自然長に戻ろうとしてエネルギーをもちます。
これって重力に似ていませんか?
重力も,物体が地面にあるときはそれ以上落下できないので,地面を基準にすると位置エネルギーは0です。
ですが,地面から少しでも持ち上げれば,物体は地面に落ちようとしてエネルギーをもちます。
冒頭で「位置エネルギーは複数ある」と書きましたが,位置エネルギーというのはこのように,「基準から位置をずらして手を離すと勝手に動き出す」ときのエネルギーの総称です。
「位置をずらしたときに生じるエネルギー」だから,略して位置エネルギー。
ばねの場合は,弾性力によって元の位置に戻ろうとするので,「弾性力による位置エネルギー(弾性エネルギー)」と呼びます。
他にも位置エネルギーはある?
ところで,重力と弾性力以外にも位置エネルギーがあるのかというと,答えはYESです。 他には何が考えられるでしょうか?
位置エネルギーをもつ力にはある共通項があります。 現時点で重力と弾性力は位置エネルギーをもつことがわかっているので,この仲間を探せばいいわけですが,このヒントだけで分かった人はすごい! 勉強したことをよく覚えていますね!
…とはいえピンとこない人のほうが多いと思います。 こちらの記事 ↓ に答えがあります!
そう,重力と弾性力は保存力と呼ばれる力でしたね!
実は,力が保存力ならば,必ずその力の位置エネルギーが計算できることが知られています。
つまり,いずれ静電気力の位置エネルギーも登場するということですね!
位置エネルギーの求め方
前回の重力の場合もそうでしたが,位置エネルギーというのは,「ずらした地点から基準に戻るまでにその力がする仕事」です。 これをもとに弾性力の位置エネルギーを求めてみましょう。
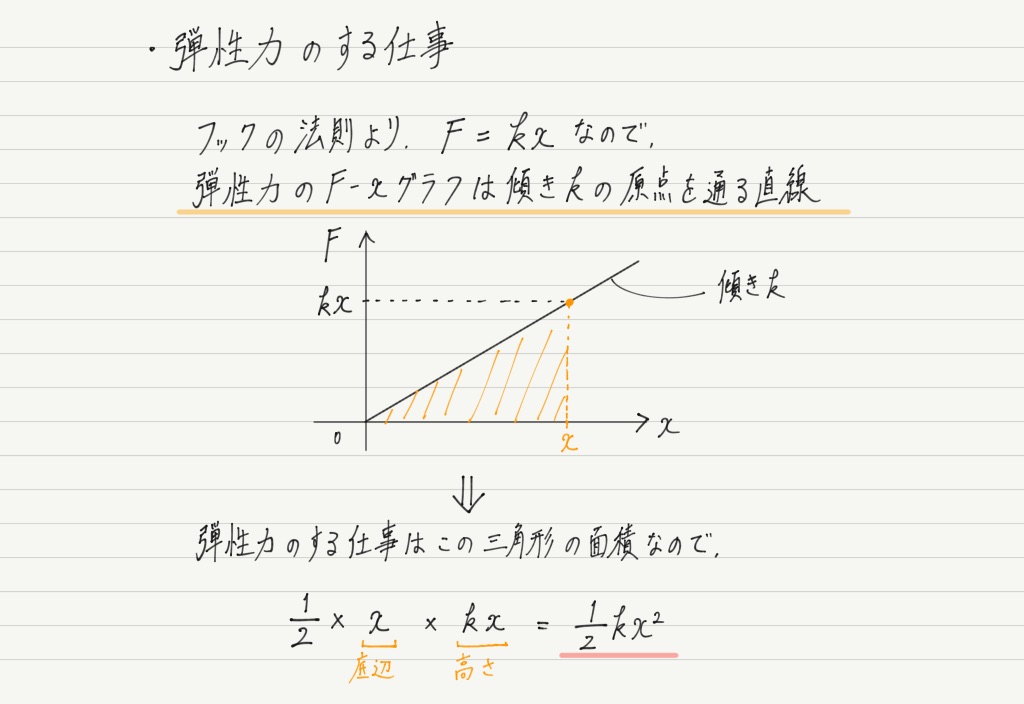
自然の長さからx[m]変形させたときの弾性力は,フックの法則よりkx[N]です。
元に戻るまでにする仕事は力(kx)×距離(x)だから,kx2?
実はこの計算は正しくありません。 どこが正しくないか指摘できますか?
答えは「ばねが自然長に戻るまでの弾性力が一定ではないので,仕事を求める式が使えない」ということです!
重力の場合は高さに関係なく大きさmgで一定でしたが,弾性力は変形量xに比例しているので,自然の長さに近づくほど弾性力は小さくなります。
そして,「仕事=力×距離」の式は,物体にはたらく力が一定でなければ使えません。
では力が変化する場合の仕事は求められないのでしょうか?
いや,あきらめるのはまだ早い。 計算で求められない場合はグラフの利用を考えましょう。
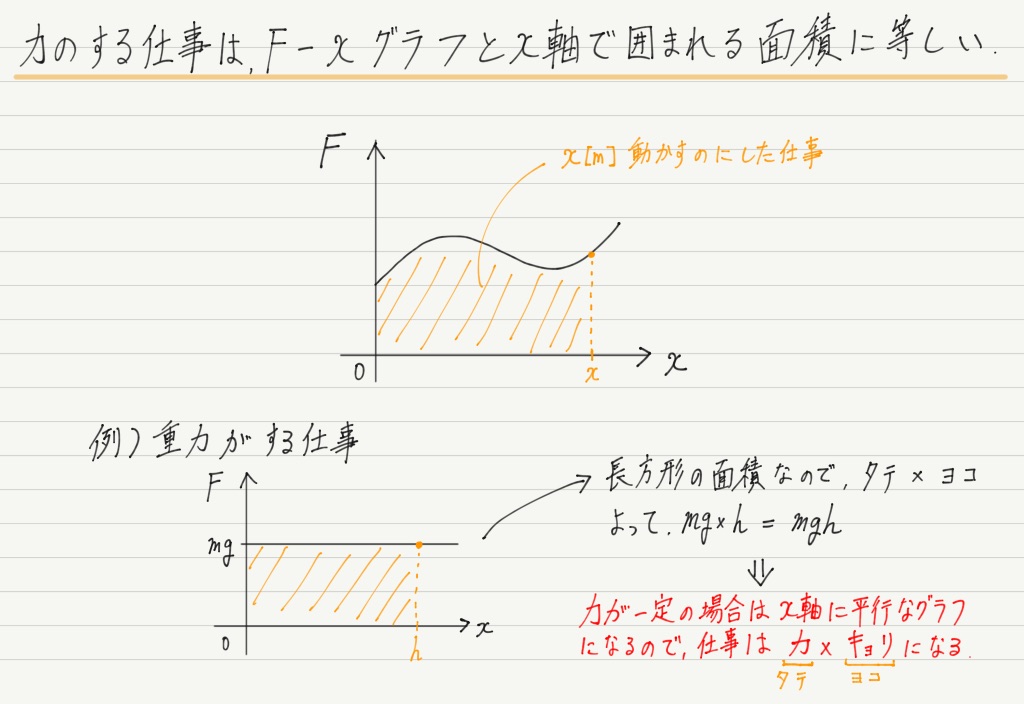
実は 力のする仕事はF-xグラフとx軸が囲む面積に等しいことが分かっています。
この事実を用いて,弾性力のする仕事を求めると,
これが弾性力による位置エネルギーの式です!!
注意点
弾性力による位置エネルギーについて2点補足します。
まず1点目。 重力の場合は位置エネルギーの基準を自由に決めていいという約束でしたが,ばねの場合は自由ではありません。
どんなときも「基準はばねの自然の長さ」です。
2点目。 重力の場合は,物体が基準より上にあるか下にあるかで位置エネルギーの符号が変わりました。
しかし,弾性力による位置エネルギーは,ばねが伸びていても縮んでいても常に正です! 間違えないようにしましょう!
今回のまとめノート
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。
次回予告
運動エネルギーと位置エネルギーが出揃ったので,次回は力学の問題を解くのには欠かせない力学的エネルギー保存の法則を説明します!