今回は道具を使ってする仕事について考察します。
何か仕事をするときに道具を使う理由はもちろん，「使ったほうが便利だから」ですが，具体的にどう便利になるのかを物理的に考察しましょう。
てこはどこを押す？
道具といっても，機械のような仕組みが複雑なものでなく，わかりやすいように原始的な道具で考えていきます。 教科書にはよく動滑車の例が載っているのですが，ここではてこを例にして話をしたいと思います。
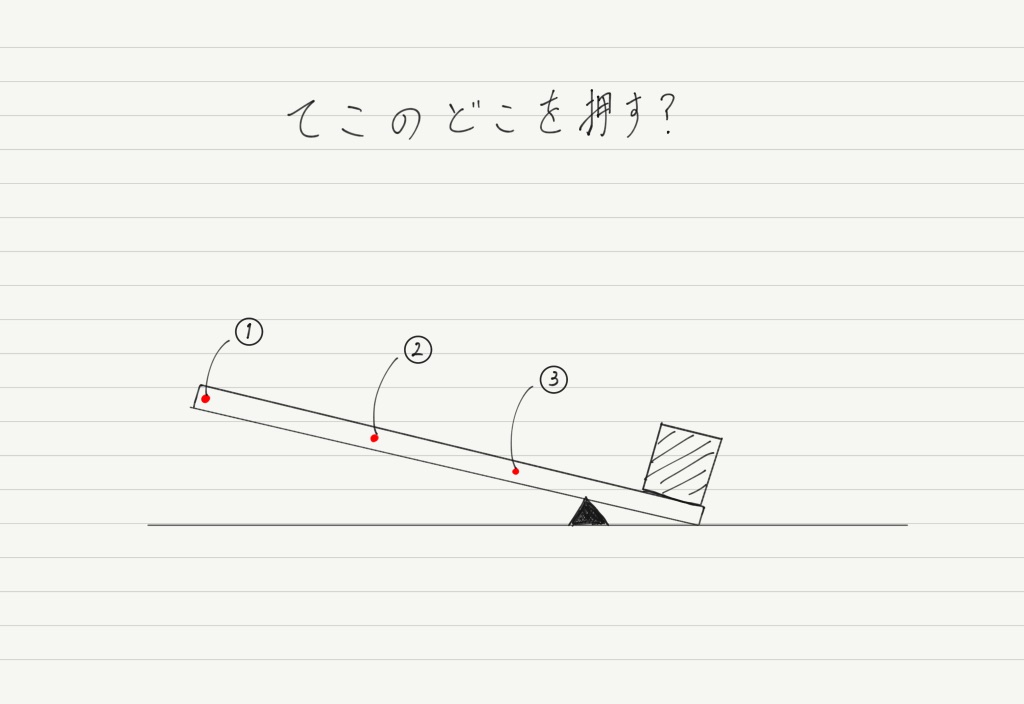
では早速ですが質問。 てこを使って物体を持ち上げようと思います。 あなたならどこを押しますか？ 下図の①〜③から選んでください！
選びましたか？ おそらく，①を選んだ人が多いんじゃないでしょうか？
①を選んだ理由は何でしょう？
もちろん「支点から遠いほうが小さい力で済むから」ですよね？
小学校で習った「てこの原理」です。
てこの原理は当然正しいのですが，ここで改めて考えてほしいのは，「本当に①を選ぶのが得策なのか？」ということ。
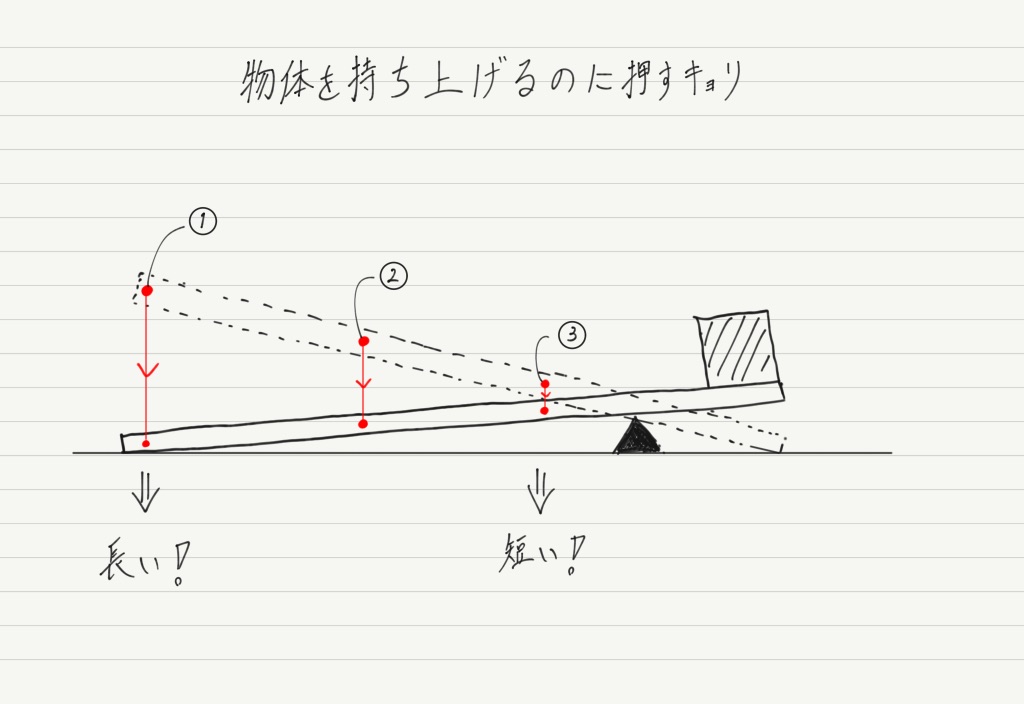
てこを一番下まで押した状態と最初の状態と照らし合わせると，
この図を見れば一目瞭然です。 てこを見ると条件反射で①を選ぶ人が多いですが，①は加える力は小さくて済むけれど，その分長い距離を押す必要があります。
一方，③は大きい力が必要ですが，短い距離で済みます。 ②は力も距離もその中間です。
小学校の理科では力に注目するので，①を選ぶのが正しい！みたいな風潮がありますが，押す距離が長くなるというデメリットを考えると，①を押すのが絶対に正しいとは言えないと思いませんか？
仕事を考えるとどこも同じ？
てこは押す力だけでなく，押す距離も考えなくてはいけないということがわかりました。
力と距離の話なので，ここで前回学んだ仕事（＝力 × 距離）の出番！
押す側にとって一番楽なのは，仕事量が一番小さくなるところを押すことです。
ということで早速①〜③で仕事を計算すると，
①を押したときの仕事＝小さい力 × 長い距離
②を押したときの仕事＝中ぐらいの力 × 中ぐらいの距離
③を押したときの仕事＝大きい力 × 短い距離
となって，どれが一番小さいのかよくわかりません。
結論を言うと，実は①も②も③もすべて同じ値になります！
道具を使って仕事をするとき，加える力が少ないと，その分動かす距離が大きくなる。 結果，道具を使わないときと仕事の量は変わらない。
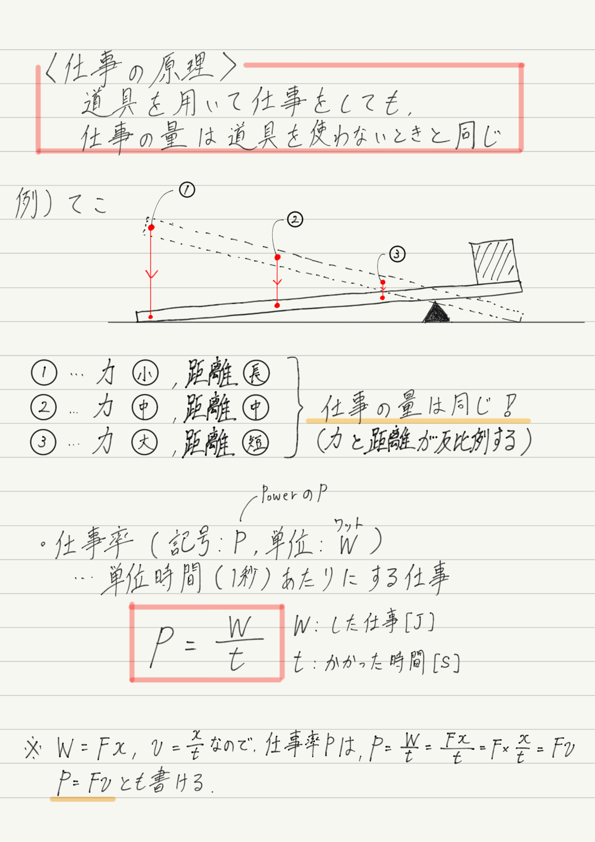
これを「仕事の原理」と言います。
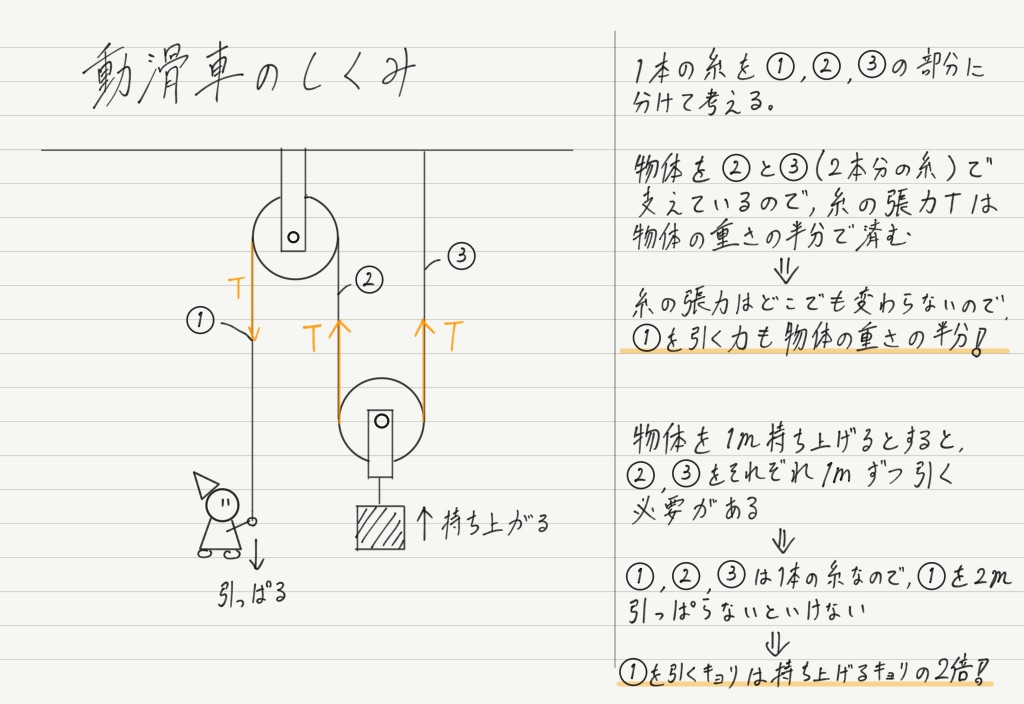
これはてこ以外のどんな道具に対しても成り立ちます。 最初に挙げた動滑車もそうです。
うーん… 道具を使っても仕事が変わらないなら，道具を使う意義はどこにあるのでしょうか？？
仕事の効率
日常生活で「仕事ができる人」といったら，それはきっと「仕事をこなすのが速い人」を指すのだと思います。 同じ仕事量なら，速くこなしたほうが効率がいいですよね！
この概念を物理における仕事にも適用します。 30秒で600Jの仕事をするAさんと，20秒で200Jの仕事をするBさんとでは，どちらが効率がいいでしょうか？
基準がないと比べられないので，時間を基準に考えます。
それぞれ１秒間にする仕事を計算してみると，Aさんの場合は，600J ÷ 30s =（1sあたり）20J。 Bさんの場合は，200J ÷ 20s =（1sあたり）10J 。
これならどちらがより効率がいいか一目瞭然！
いま求めたような，１秒間あたりの仕事を「仕事率」と呼び，単位はW（ワット）で表します。
つまり，AさんとBさんの仕事率はそれぞれ20Wと10Wということで，仕事率が大きいAさんの方が効率がいいと判断できます。
余談ですが，仕事率を英訳するとPowerです。 昔は仕事率を「馬何頭分か」で表していた（いわゆる馬力というやつ）ので，それに由来しています。
普段の感覚だと，Powerは「力」と訳したくなりますが，物理ではそれは間違いなので注意してください（物理でいう「力」は，英語ではForce）。
てこの問題ふたたび
仕事率の概念を学んだところで，最初の問題に戻りましょう。「てこのどこを押すか」問題です。
仕事の原理により，どこを押しても仕事の量は変わらないことが分かりました。
しかし，仕事の量は変わらなくても，仕事率は変わる可能性があります！
いくら加える力が小さいとはいえ，動かす距離が大きければ，そのぶん仕事を終えるのに時間がかかってしまいます。 動かす距離もなるべく小さいほうがいい。
つまり，「自分が無理なく押せる範囲で，もっとも支点に近いところ」を押せば仕事率が最も大きくなり，これが賢いてこの使い方といえるでしょう！
とにかく端っこを押せばいい！という短絡的な発想からは卒業しましょうね！
今回のまとめノート
最後のP＝Fvはそんなに使わないけれど，教科書には書いてあるので一応載せました。
時間に余裕がある人は，ぜひ問題演習にもチャレンジしてみてください！ より一層理解が深まります。
次回予告
次回は，力の話に一度戻ります。
