いよいよエネルギーの分野に入ります!
エネルギーそのものの話をする前に,まずは力のする仕事について学んでいきましょう。 仕事という単語は力学に限らず,物理のあらゆる分野に登場します。
用語の意味があやふやなままだと,他の分野にも支障が出てしまうので,ここでしっかりと意味を確認しておきましょう!!
物理における「仕事」とは
「仕事」という単語は普段いろいろな意味で用いられますが,物理において,「仕事をする」とは,「力を加えて物体を移動させること」を意味します。
物理の教科書で仕事という単語はこの意味でしか使われていませんので,勝手な解釈を入れないようにしましょう。
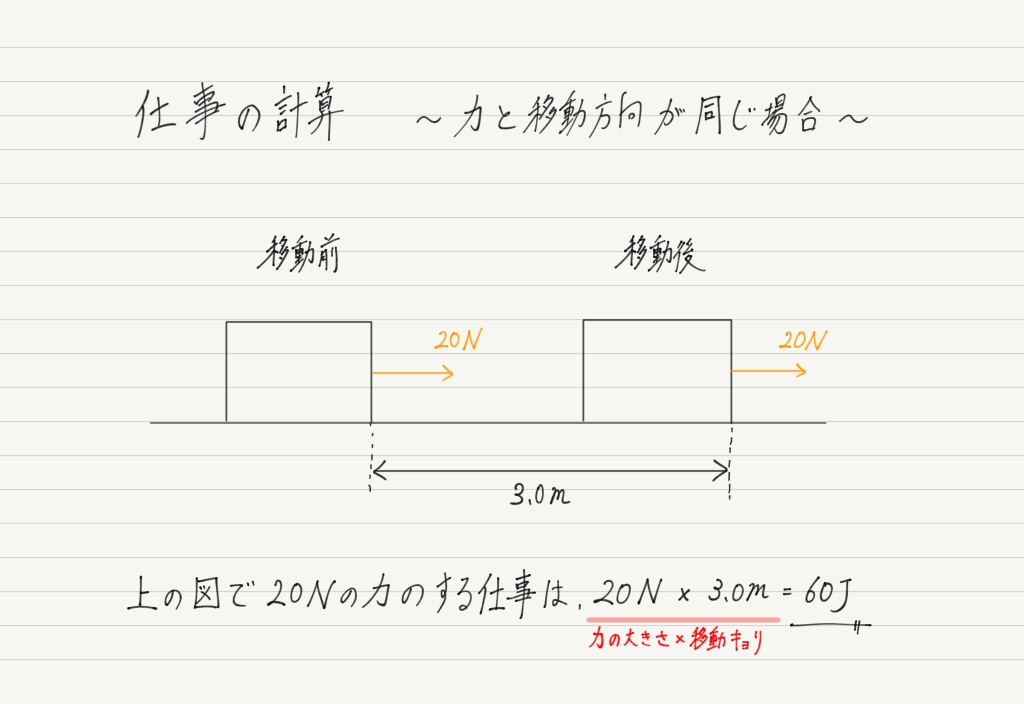
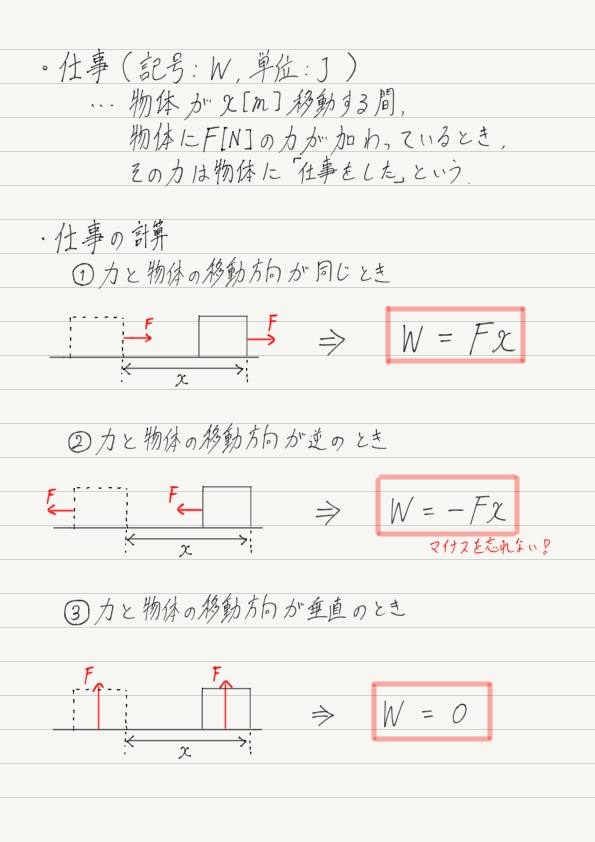
仕事の量は「力の大きさ × 移動距離」で計算でき,単位にはJ(ジュール)を用います。
これだけでは説明不足なので,例題を交えながらもう少し詳しく仕事について見ていきましょう。
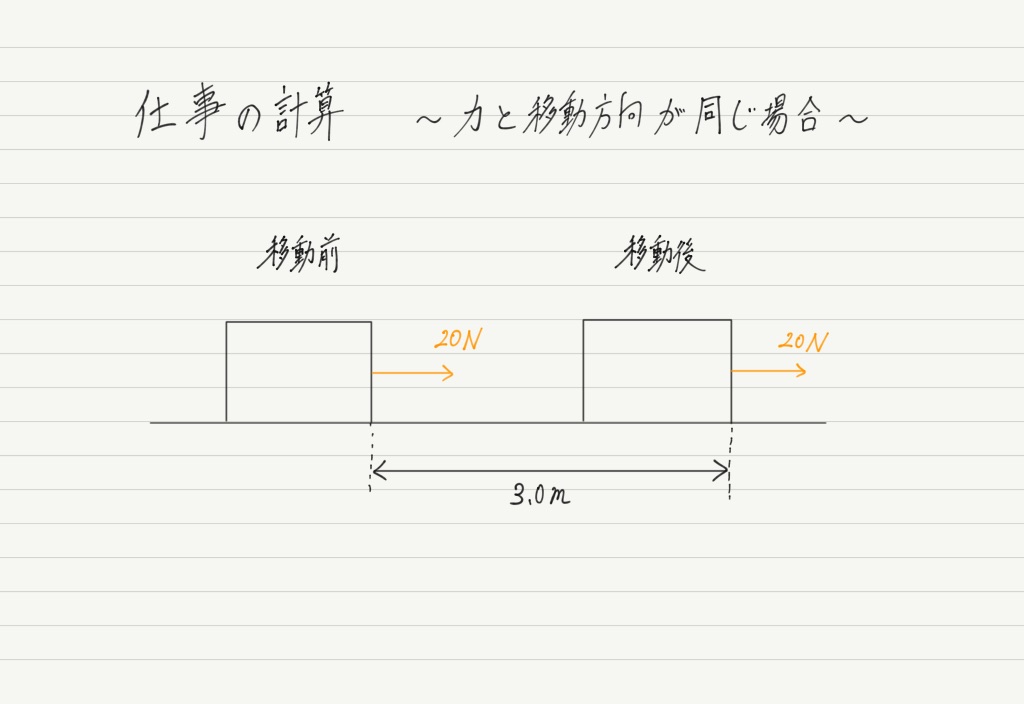
① 力の向きと移動する向きが一致している場合
まずは一番基本となるパターンから。
上図のように右向きの力に対し,物体の移動方向も右だった場合は「力の大きさ × 移動距離」で,この力のした仕事が計算されます。
たったこれだけ。 簡単!
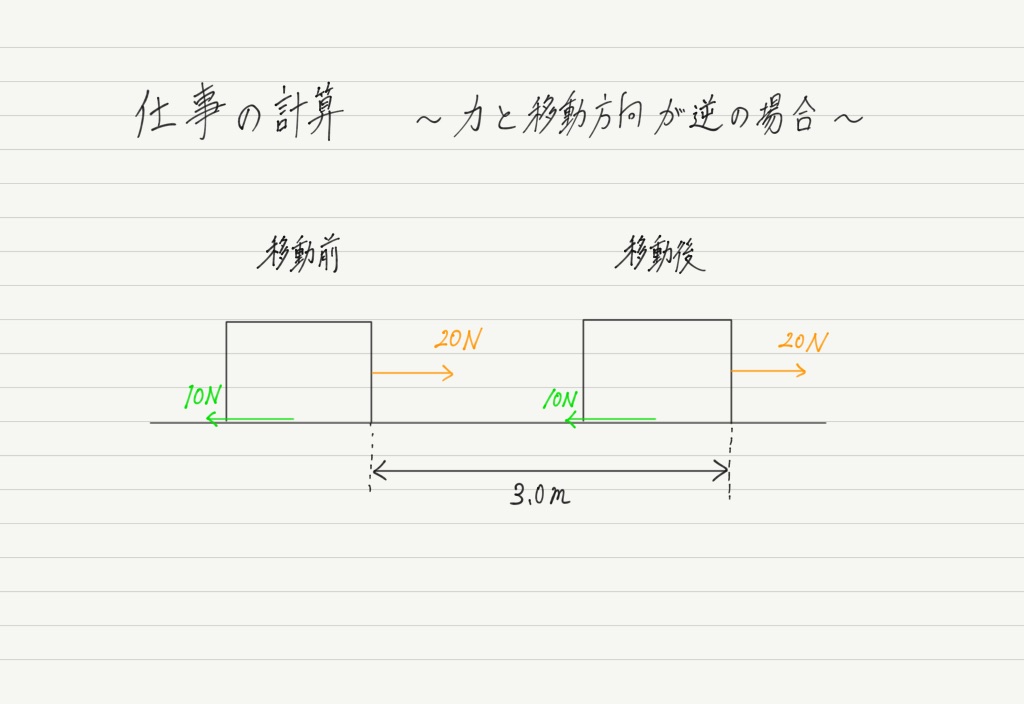
② 力の向きと移動する向きが反対の場合
①で物体を右向きに動かしたのは,物体に加えた右向きの力です。
「力のする仕事」と言うと,「物体を動かした力のする仕事」のことだと思いがちですが,実は,物体を動かした力以外の力でも仕事は計算できます。
たとえば,①の問題で床との間に摩擦があるとしましょう。
この動摩擦力は物体を動かすどころか,むしろ運動を邪魔しています。
このような力についてもちゃんと仕事が計算できるのです!!
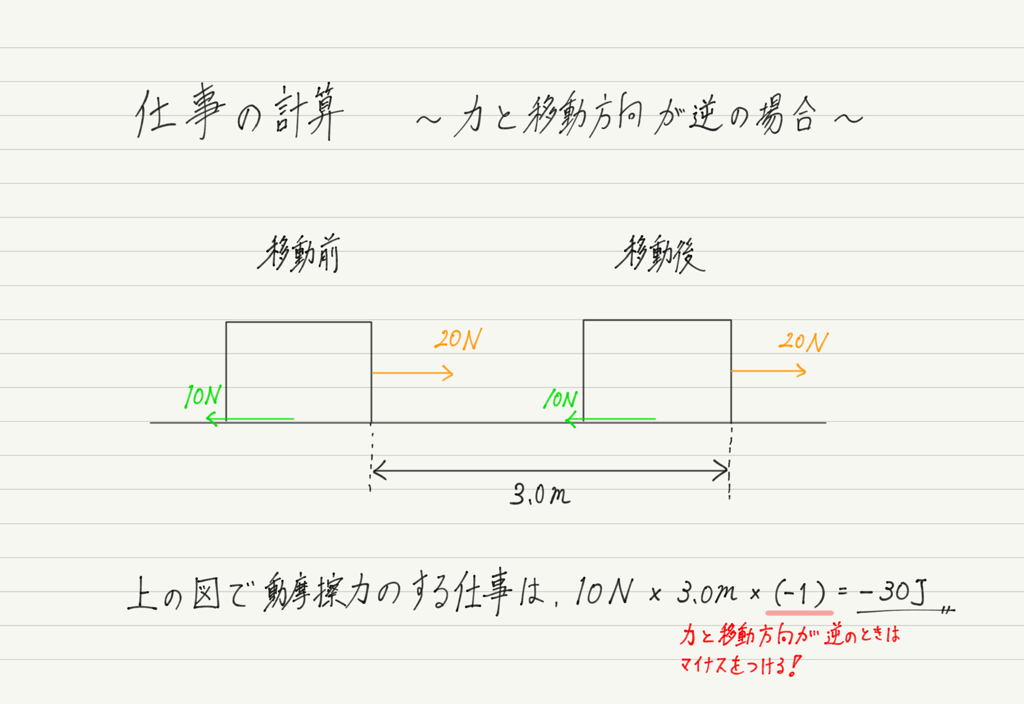
計算式は変わらず「加えた力 × 移動距離」ですが,物体の移動と逆向きの力の場合,計算で出た答えにマイナスをつけてください。
仕事には,正の仕事と負の仕事があって,その力が物体を動かすのに貢献していれば正の仕事,邪魔をしていれば負の仕事,と考えてください。
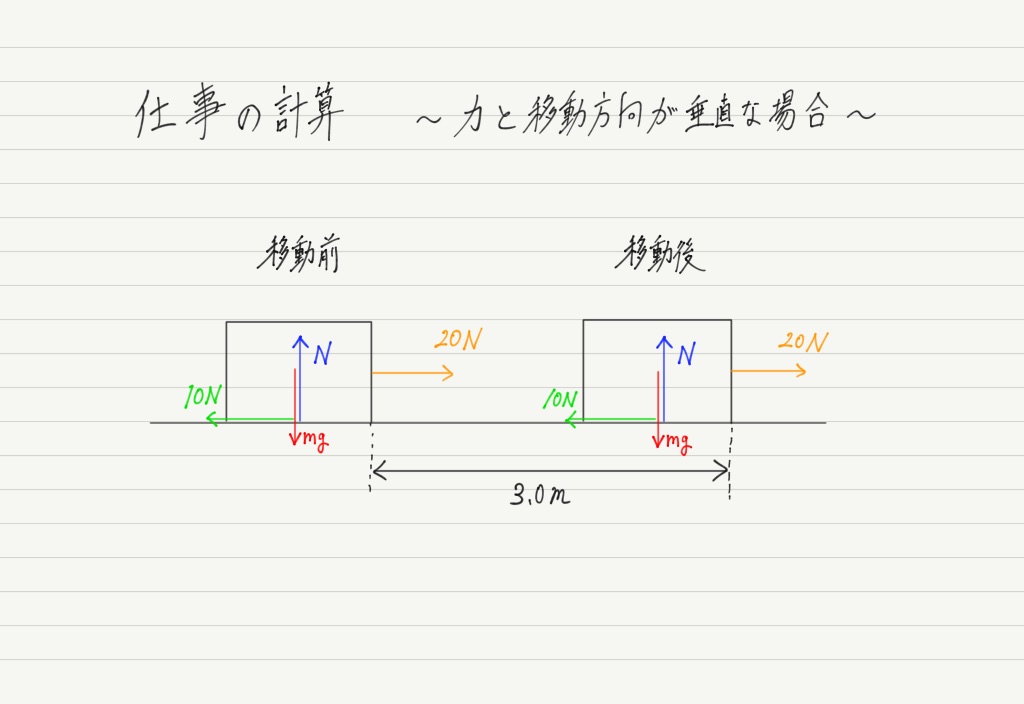
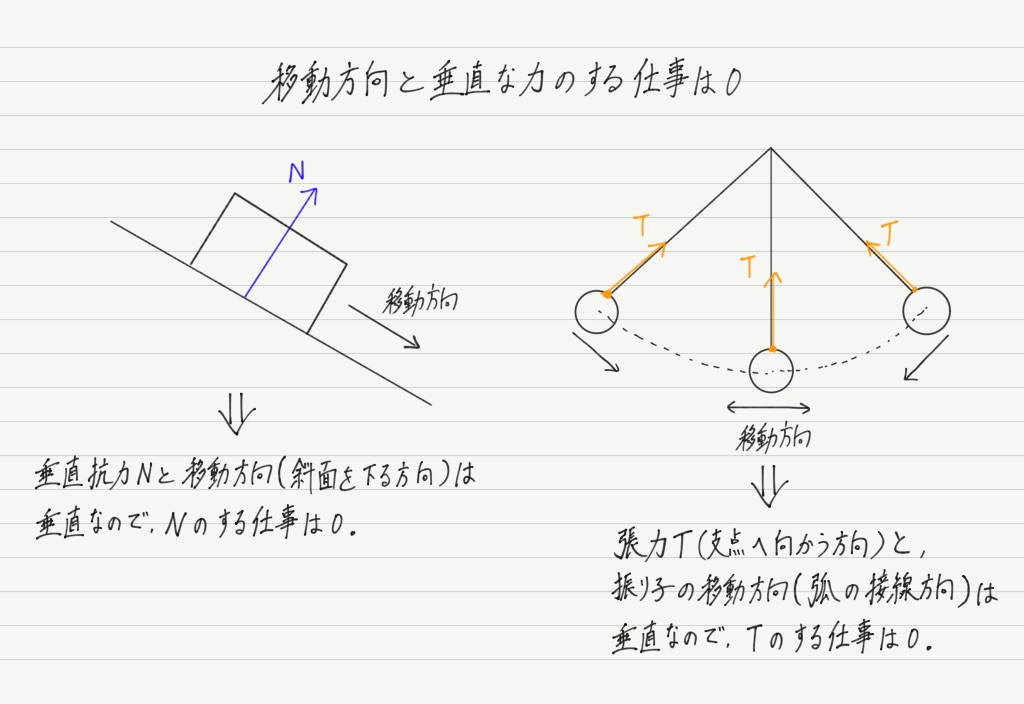
③ 力の向きと移動する向きが垂直な場合
最後に力と移動方向が垂直な場合です。
いま考えているシチュエーションでは,重力や垂直抗力が移動方向に対して垂直です。
実は仕事が一番簡単に求められるのはこの垂直な場合。
なぜなら,移動方向と垂直な力のする仕事は必ず0になるから!!
力が何Nでも,移動距離が何mでも,垂直ならば仕事は0。
②のところで,力が物体を動かすのに貢献していれば正の仕事,邪魔をしていれば負の仕事,と書きましたが,垂直な力は物体の動きに貢献も邪魔もしていませんよね? だから0なのです。
注意点
仕事の計算に関していくつか注意しておきます。
まず1つ目。 物体に力を加えても,物体が動かなければ仕事は0です(仕事=力 × 移動距離なので,移動距離が0なら仕事も0)。
日常生活ではよく「仕事をがんばった」と言いますが,物理の世界ではいくらがんばっても物体が動かなければ仕事をしたことにはなりません(シビアな世界!)。
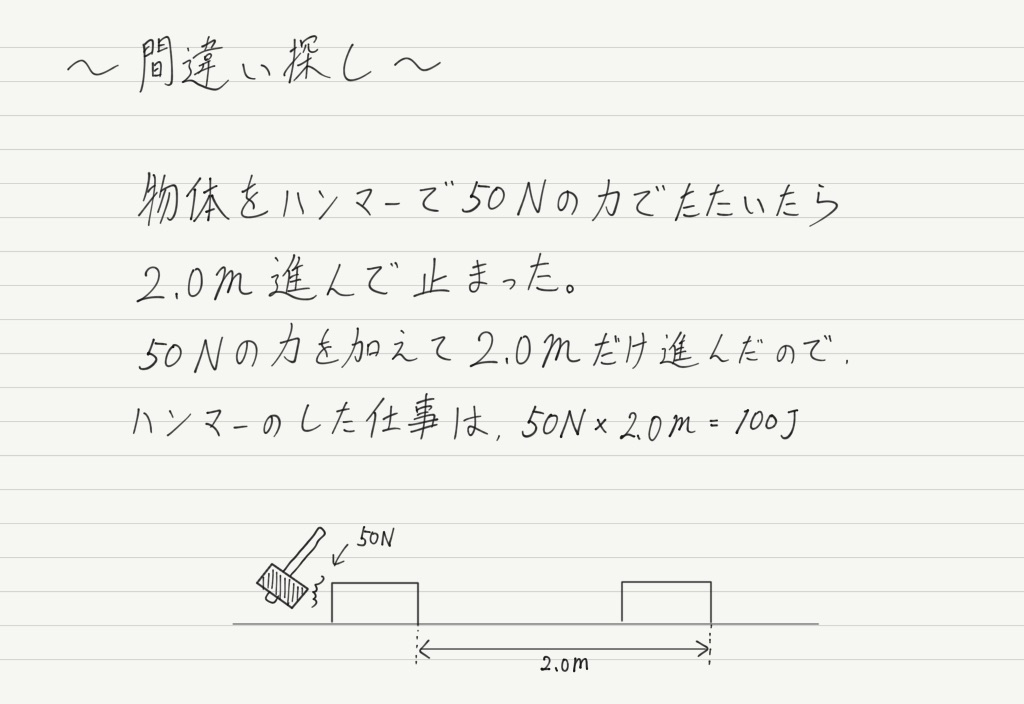
2つ目。 以下の解答は間違っています。どこが間違いなのか考えてみてください。
冒頭で「仕事をする=力を加えて物体を移動させる」と言いましたが,仕事を「力 × 移動距離」で計算するためにはひとつ条件があります。
それは,「物体が移動している間,ずっとその力が加わっていること」です。
上の図では,確かに力を加えて物体を動かしていますが,その力が加わっているのは最初の一瞬だけで,物体はその勢いで動いただけです。 このような場合,力と移動距離をかけても仕事の計算にはなりません!
3つ目。 これは理系に進む人は特に重要。
物理をやる上でベクトルとスカラーの区別は重要ですが,仕事はベクトルではなくスカラーです!!
ベクトルとスカラーがよくわからない人はこちらの記事↓で詳しく解説しています。
スカラーということは,仕事には向きがありません。
②で負の仕事が出てきましたが,このマイナスは「逆向き」を表すマイナスではなく,「0より小さい」ことを表すマイナスということになります(つまり,②の答えを「左向きに30J」と書いたらアウト!)。
仕事は移動方向や力の向きの話と一緒に説明されるので,「仕事にも向きがあるのかな?」と勘違いする人が多いです。 気をつけましょう!
今回のまとめノート
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。
次回予告
仕事の話はまだ続きます。 道具を使って仕事をするメリットについて考えてみましょう。