引き続き運動の第2法則のお話です。 前回は法則の中身がメインでしたが,今回は計算中心。
「物体に生じる加速度は,加えた力の大きさに比例し,質量に反比例する」
前回はこれをF=maという式の形で表しました。 この式は一体何に使えるのでしょうか?
運動の法則の式をどう使うか
F=ma 。この式をよーく見てください。。。
等式なので,文字に数値を代入すれば未知の値を求めることができます。 例えば,質量mと加速度aの値が分かっていれば,この式に代入することで,力Fが求められますよね!!
ここで,いままでに習ったことを思い返してみてください。
物体にはたらく力Fは,重力ならmg, 弾性力ならkxというように,計算方法をすでに学習しているので,個別に求めることが可能です。 質量mは,重量計を用いればすぐに計測できます(すごく軽い or すごく重い場合は簡単ではないかもしれませんが)。
つまり!!
運動の第2法則の式F=maは,Fとmを代入して,aを求める,といった使い方ができるということです!!
F=maと表記すると,「Fを求める式」に見えてしまうので,今後この式は,「ma=F」と書くことにしましょう。 左辺と右辺を入れ替えただけですが,「Fは求めるものではなく,代入するもの」というニュアンスが出ていると思いませんか?
この式は「運動方程式」と呼ばれるもので,物理を学ぶ上で,すごーーーーーく大切な式になります!!
運動方程式で物体の過去や未来がわかる!?
繰り返しになりますが,この式は 「mとFを代入して,aを求める」といった使い方をします。 つまり,aという解を求める方程式です。
普通の方程式なら,解を求めてハイおしまい,なんですが,運動方程式の場合,解を求めることが非常に重要な意味をもちます。
具体的な計算を始める前に,まず運動方程式の意義を理解しましょう!
物体にはたらく力 F が一定ならば,物体は等加速度運動をします(※ Fは一定でなくても運動方程式は使えますが,わかりやすさを優先します)。
等加速度運動ならば,以前やった3つの式を用いて,「スタートしてからt秒後の速度」や,「t秒後の位置(変位)」を求めることができます。
が,等加速度運動の式を使うには加速度aを代入しなければいけません。 加速度を直接求めるのはけっこう大変です。 そこで運動方程式の出番。 直接求めるのが難しいaも,運動方程式なら計算で簡単に求められます!
運動方程式に必要なのは,質量mと物体にはたらく力Fです。
以上の話をまとめてみると,「物体の質量mと,はたらく力Fさえ分かれば,その物体のt秒後の速度や, t秒後の位置をすべて計算で求めることができる」ということになります!
これってすごくないですか!!!!
運動方程式を解くと,その物体がこれまでどんな運動をしてきたか,この先どんな運動をするのかが分かる,ということです!
もっとも重要なのは,運動方程式はどんな物体でも成り立つという点。
物理基礎の問題では,滑車で吊るされた物体とか,斜面上を滑る物体とか,あまりおもしろくない問題しか出てこないのですが,運動方程式の適用範囲はそんなものではありません。
たとえば星の運動だって運動方程式で計算できます。「次に日本で皆既日食が次に見られるのは◯年後の◯月◯日」みたいなニュース見たことありませんか?
なんでそんな未来のことが分かるのかというと,太陽や月の運動を運動方程式を使って計算しているからです。 こんな計算もできちゃう運動方程式を学ぶなんてワクワクしますよね!
実践:運動方程式をどう立てるか
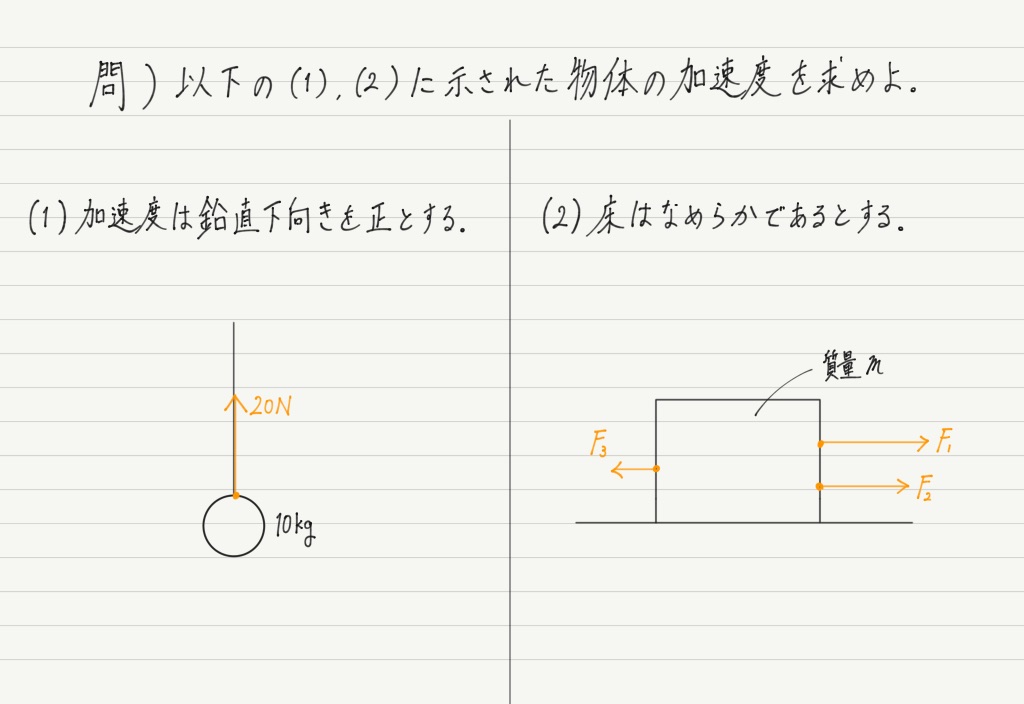
では,具体的な問題を例に運動方程式を立ててみましょう。
力が関係する問題で,「加速度を求めろ」と言われたら,まず運動方程式を思い浮かべてください。
さて,運動方程式で大事なのは,解くことよりも式を立てること。 運動方程式の立て方の手順を紹介します!
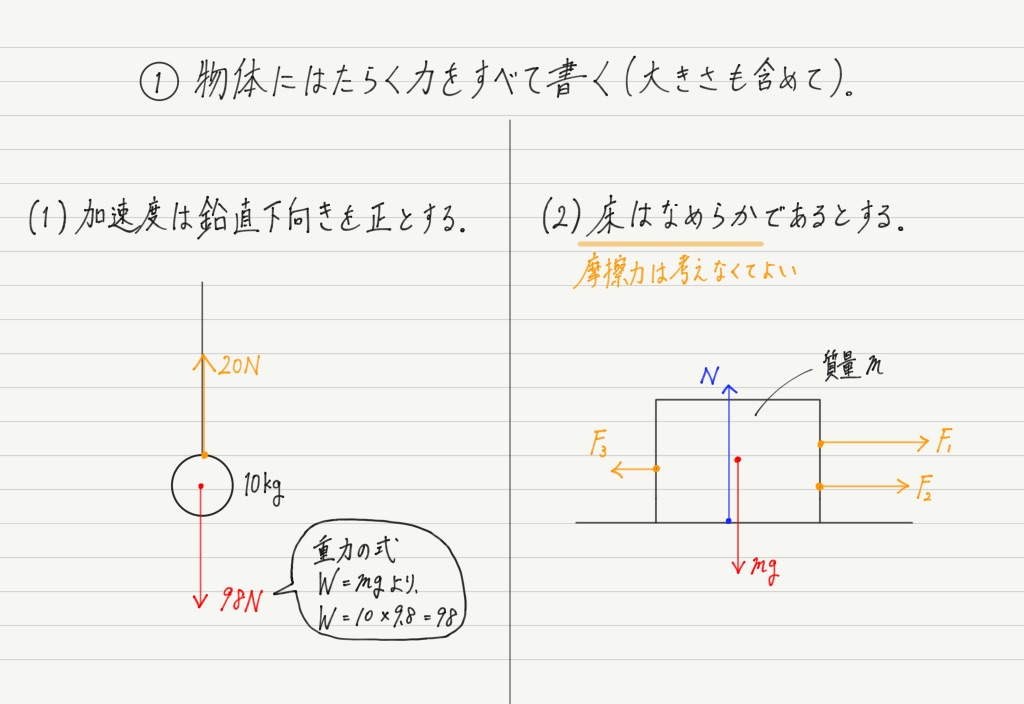
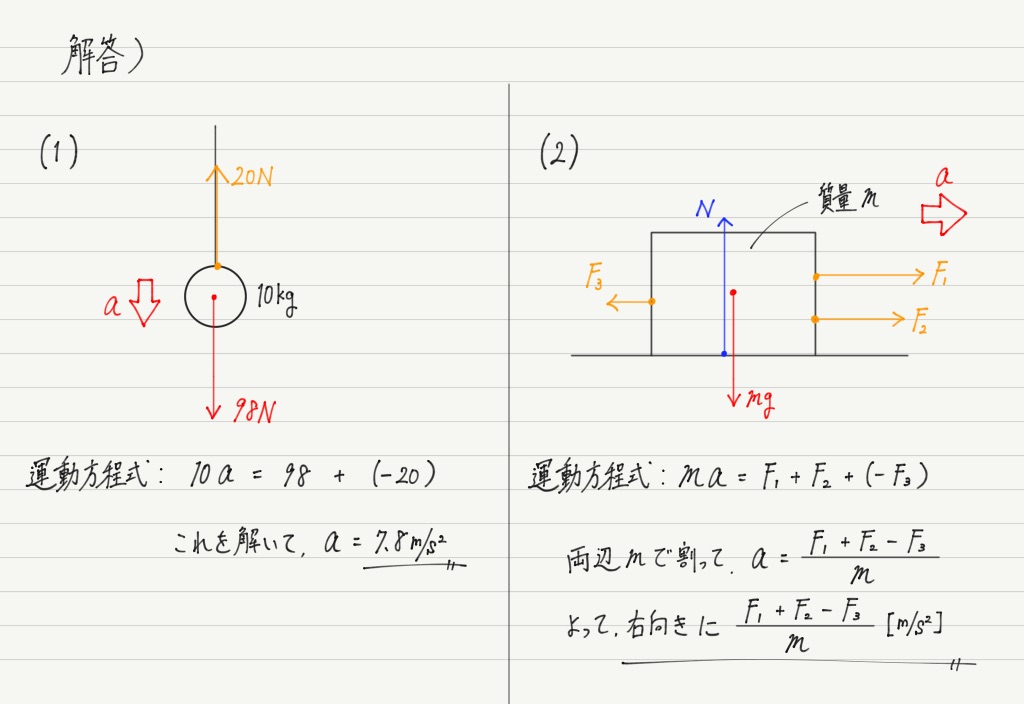
では実際に手順通りやってみましょう。 まずは物体にはたらく力を書き込みます。
すでに与えられている力もあるので,それ以外の力を書きこんでいきましょう。
(1)のように数値が与えられていれば,重力の大きさはW = mgで計算できるので,それも書いておきます。
(2)のように,質量などが文字で与えられている場合は,そのまま文字で記しておきましょう。
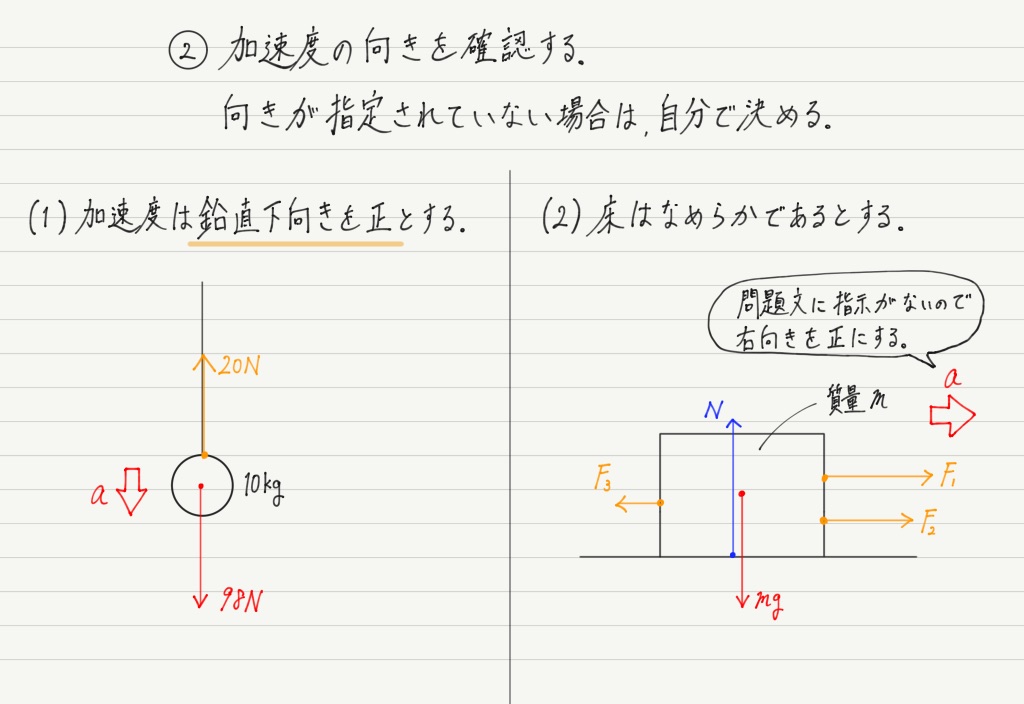
これで物体にはたらく力はすべて書き終えたので,次に加速度aの向きをチェックします。
(1)は問題文に鉛直下向きとありますが,(2)は何も書かれていません。 何も書かれていない場合は,自分で加速度の向きを設定します。
この向きは自分で決めて構いませんが,「じゃあ,上にしようかな」などと,テキトーに決めてはいけません! 少なくとも,物体が動く可能性のある方向にしてください。
今回の場合は物体が左右に引っ張られているので,動くとしたら右か左です。 右か左(問題によっては上か下)の2択に絞ったら,あとはどっちでもOK。
今回は右向きを正にしてみましょう。
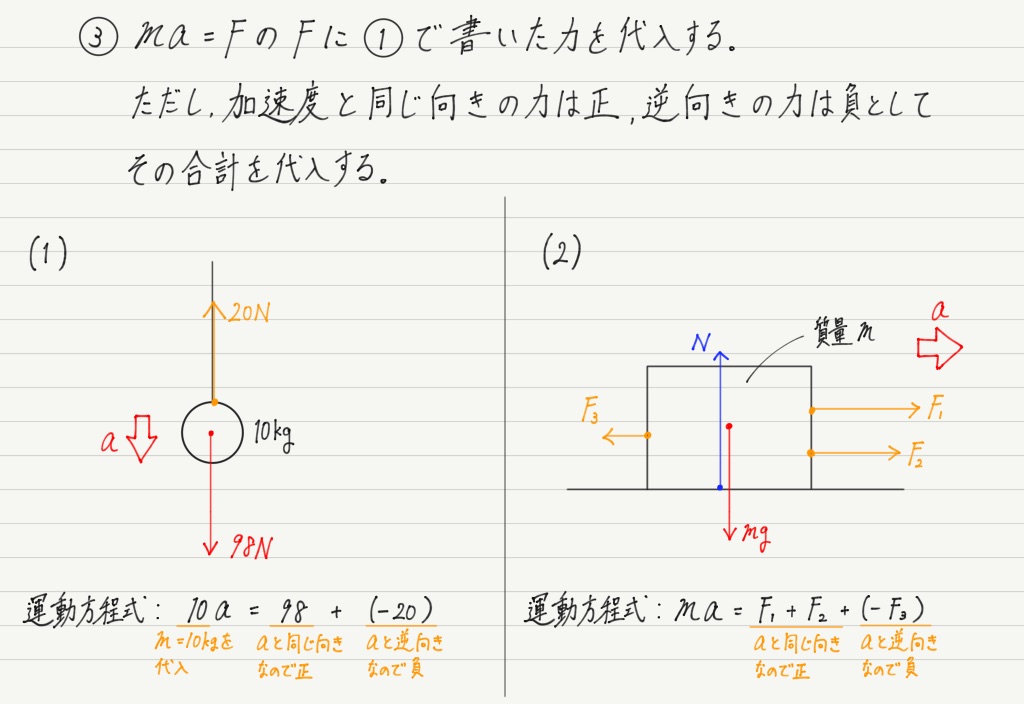
これで準備完了です!! いよいよ手順③,運動方程式を立てます。
運動方程式の形は,ma=Fですが,左辺のmaはどんな物体がどんな運動をしていようとそのままです。
したがって,「運動方程式を立てよ」と言われたら,どんなときでも「ma =」と書き始めて構いません。
(1)は質量が10kgと与えられているので,mに10を代入しましょう。
さあ,問題は右辺です。右辺のFは物体にはたらく合力なので,先ほど書き込んだ力を合計していくことになります。
ただし力は向きがあるので,ただ足せばいいわけではありません。
手順②で確認した加速度の向きを基準にして,逆向きの力にはマイナスを忘れずにつけてください。
(2)の運動方程式を見て「mgとNは書かなくていいの?」という声が聞こえてきそうですが,今回の問題ではmgとNは運動方程式に含めません。
なぜかというと,(2)では物体は右か左に動くからです。 上向きや下向きの力をいくら加えても,左右の動きには何の関係もありません。
なので,運動方程式の右辺に,加速度と垂直な方向の力は含めません!
「使わないなら最初からその力は書かなくていいじゃないか」という人をたまに見かけますが,それはちがいます。 運動方程式には使わなくても,別の計算で使うことは大いにありえますから,手順①では使う・使わないに関係なく,物体にはたらくすべての力を書くようにしてください。
さぁ,ここまで終われば,運動方程式は完成です!! 運動方程式を立てたら,あとは解く(aを求める)だけ。
(※(1)は鉛直下向きが正と問題文に書いてあるが,(2)は向きを自分で勝手に決めたので,答えにちゃんと向きも書いておく)
えっ?これだけ??
ハイ,これだけです。「運動方程式を立てる」と聞くと難しそうに聞こえますが,実際にやることは,力を書いて,符号を付けて足すだけ。
ただ,力を書き忘れたりすると計算が違ってきちゃうので,物体にはたらく力だけはしっかり書けるように練習しましょう!!
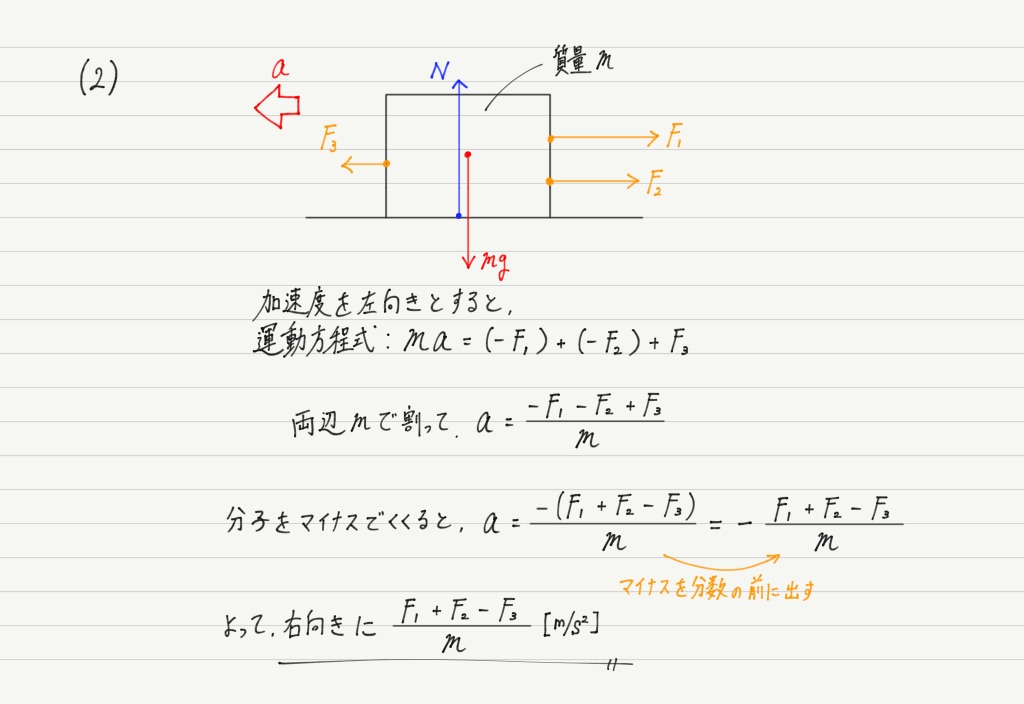
だいぶ長くなってしまいましたが,ついでにもう1つ。 上の(2)で,もし加速度を左向きにしたらどうなるでしょうか?
左向きを正にして計算してみたら,答えにマイナスが付く…。
つまり加速度は右向きじゃん!ってことで,aを左向きにしてもちゃんと正しい答えにたどり着きます。
このように加速度の向きをまちがって逆に決めてしまっても,答えがマイナスになって,「ああ,最初に決めた向きは逆だったのか」で済む話です。 加速度の向きを決めるときはあまり深く考えなくても大丈夫ということですね!
今回のまとめノート
前回と今回の記事の分量からもわかる通り,運動方程式は本当に大事なので,問題を解いて確実にマスターしてください!!
次回予告
次回からはエネルギー分野に突入します。