前回の続きで，今回も摩擦についてのお話です。 前回のおさらいも兼ねて，もう一度イメージしましょう。
目の前に，がんばって押せばなんとか動かせるぐらいの質量をもつ物体があります。 その物体を初めは弱い力で押し，徐々に力を大きくします。 さぁ，イメージしてくださいね！！
まず，弱い力を加えているときは物体は動きません。 押す力と静止摩擦力がつりあっているからでした。
しかし，静止摩擦力の大きさには限界（＝最大摩擦力）があるので，加える力を大きくすると物体は動き出します。 「加えた力＝最大摩擦力」になるときが動き出す瞬間です。
と，ここまでが前回の内容でした。 今回は，動き出したあとの摩擦力について学びましょう！
物体が動いているときの摩擦力について
加える力が最大摩擦力を超えると物体は動き出しますが，摩擦力が消えたわけではありません。 消えてはいませんが，実は摩擦の種類が変わっています！
動き出すまで，物体には静止摩擦力がはたらいていましたが，動き出したあとは「動摩擦力」と呼ばれるものに変わります。 その名の通り，「動いている物体にはたらく摩擦力」です。
動いているのを邪魔する方向にはたらく力。 みなさんのもっている摩擦力のイメージに近いのでは？
さて，動摩擦力の大きさ f’ は最大摩擦力同様，計算で求められます。
式は，f’ = μ’ N です。
ところで，最大摩擦力の大きさ f を求める式は f = μ N でした。 ともに垂直抗力 N に比例する格好になっていて，とても似ています！
ただ唯一，比例定数の部分が異なっていることに注意しましょう。
２つの摩擦係数の関係
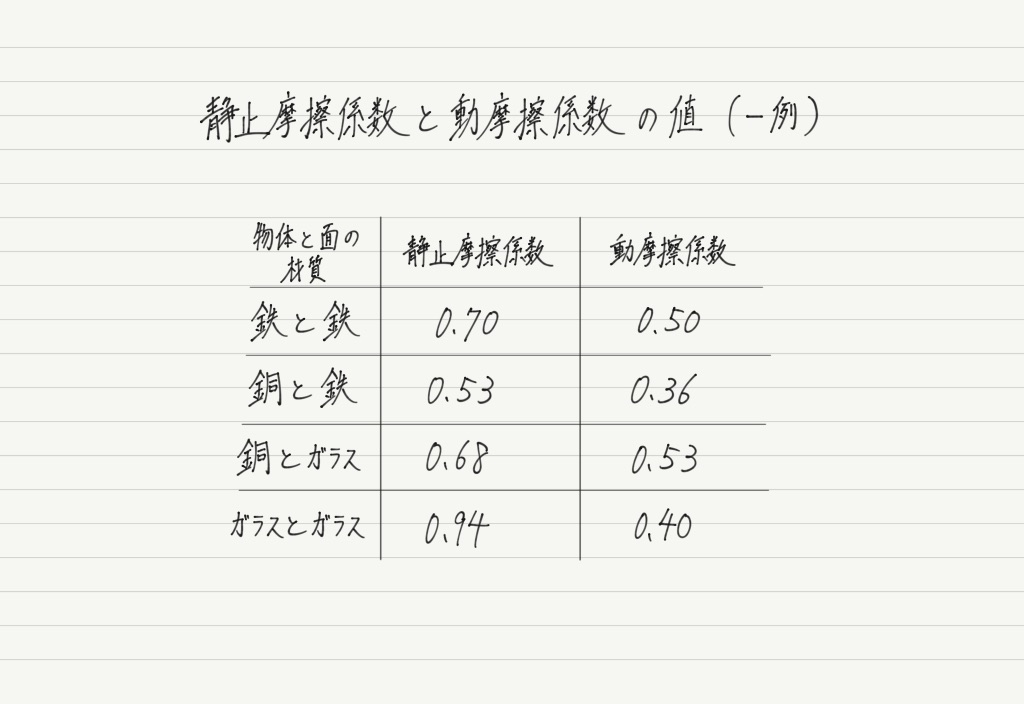
μ’ は動摩擦係数と呼ばれるもので，静止摩擦係数 μ と同様に，物体とそれが接触している面の材質によって決まります。 いくつか例を挙げてみましょう。
上の表で静止摩擦係数と動摩擦係数の大小関係に注目してください。
すべて，μ > μ’ になっていますよね！
これは上に挙げた例がたまたまそうなっているのではなく，すべての材質において，動摩擦係数は静止摩擦係数よりも必ず小さくなるのです。
重たいものを押して動かすとき，動き出すまでは大変だけど，いったん動き出してしまえばそのあとは楽。 そんな経験ありませんか？ これは動摩擦係数が静止摩擦係数より小さいことが原因なのです。
最後に，これは動摩擦力の式から明らかですが，動かしている間，動摩擦力の大きさは一定になります（途中で面の材質や垂直抗力の大きさが変わったら別ですが…）。
これは，加える力によって大きさが変わる静止摩擦力との大きな違いです。
今回のまとめノート
数回に渡って色々な種類の力を紹介してきましたが，これにていったん終了です。 時間に余裕がある人は，ぜひ問題演習にもチャレンジしてみてください！ より一層理解が深まります。
次回予告
次回は力の取り扱いについてみていきましょう。
