前回の記事では物体を投げ下ろす運動を扱ったので,今回は物体を投げ上げる運動を扱いたいと思います!
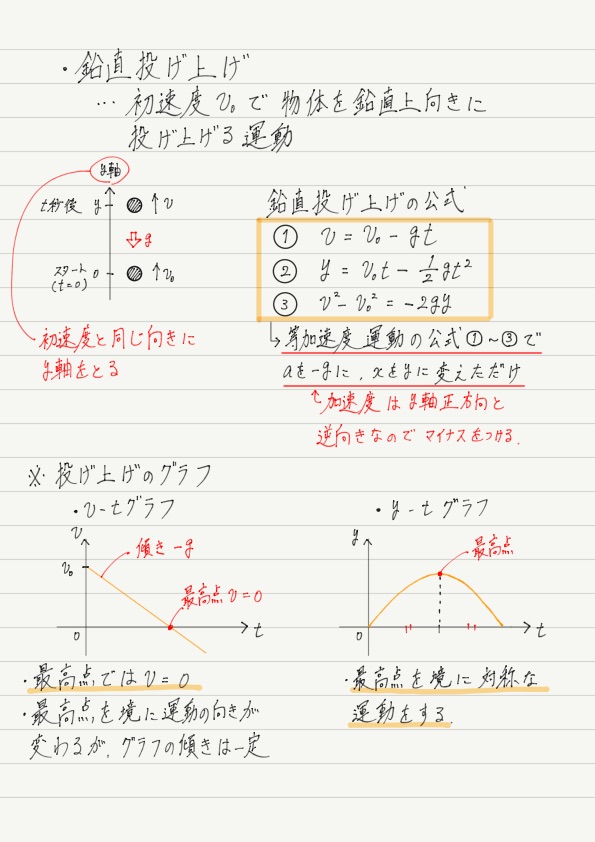
鉛直投げ上げ(鉛直上方投射)
上に投げ上げた物体は最高点に到達した後,折り返して落下するので,これも落下運動の一種になります。
投げ上げは途中で運動の向きが変化するので一見すると難しそうですが,大事なのは上向きに運動しているときも下向きに落下しているときも,物体は重力だけを受けて運動しているということ。
つまり,鉛直投げ上げも等加速度運動であるということです。 図で見てみましょう!
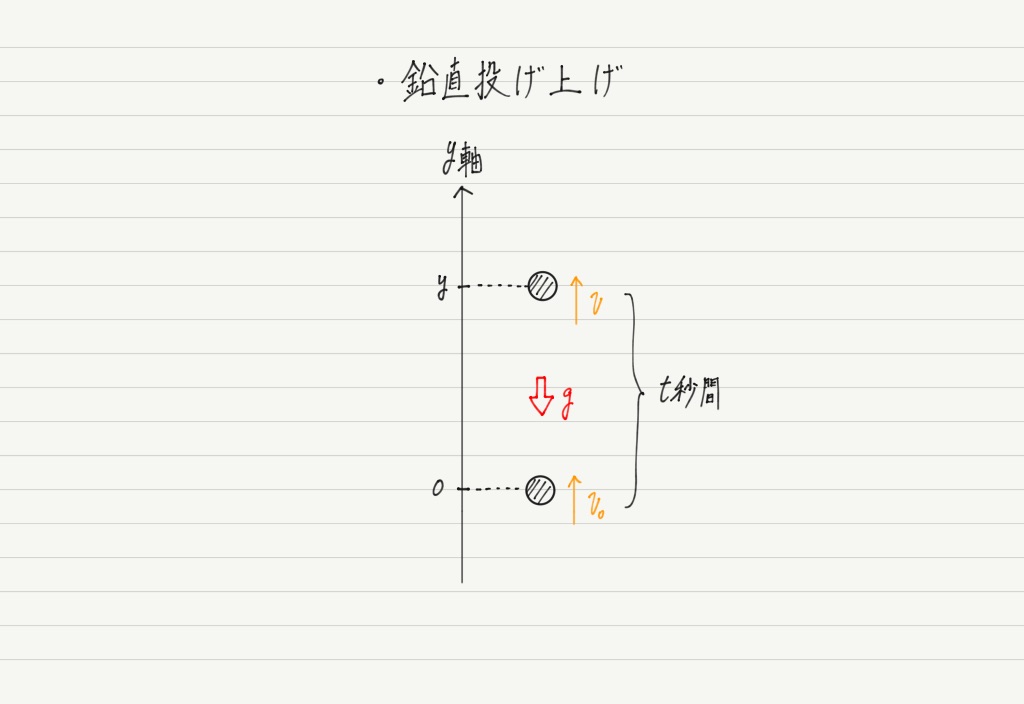
まず,y軸の向きに注目してください。前回の投げ下ろしのときは下向きを正としていましたが,今回は上向きを正とします。
上向きが正なので,重力加速度は負の向きに生じています。
「マイナスがつくのは面倒だから,やっぱり軸は下向きが正の方がいいのでは?」と考え直したくなりますが,そうすると今度は初速度の方にマイナスが付いてしまって堂々巡り。
このようにどっち向きを正にしても,結局マイナスからは逃れられません。 このような場合,慣習として「初速度の向きを正にとる」ことになっているので,素直にそれに従うことにしましょう。
話を戻しましょう。 鉛直投げ上げの運動は上の図のとおり負の重力加速度をもつ等加速度運動となります。 よって鉛直投げ上げの式は,
となります。 加速度の記事でも説明しましたが,加速度につくマイナスは,「正の方向に減速」を意味する場合と,「負の方向に加速」を意味する場合の2つがあります。
鉛直投げ上げの場合は,投げ上げてから最高点までは「正の方向(上向き)に減速」の意味で,最高点を過ぎたあとは「負の方向(下向き)に加速」です。
投げ上げは運動の最中,加速度はずっと −g で一定ですが,最高点を境に意味が変わることに気をつけてください。
鉛直投げ上げのグラフ
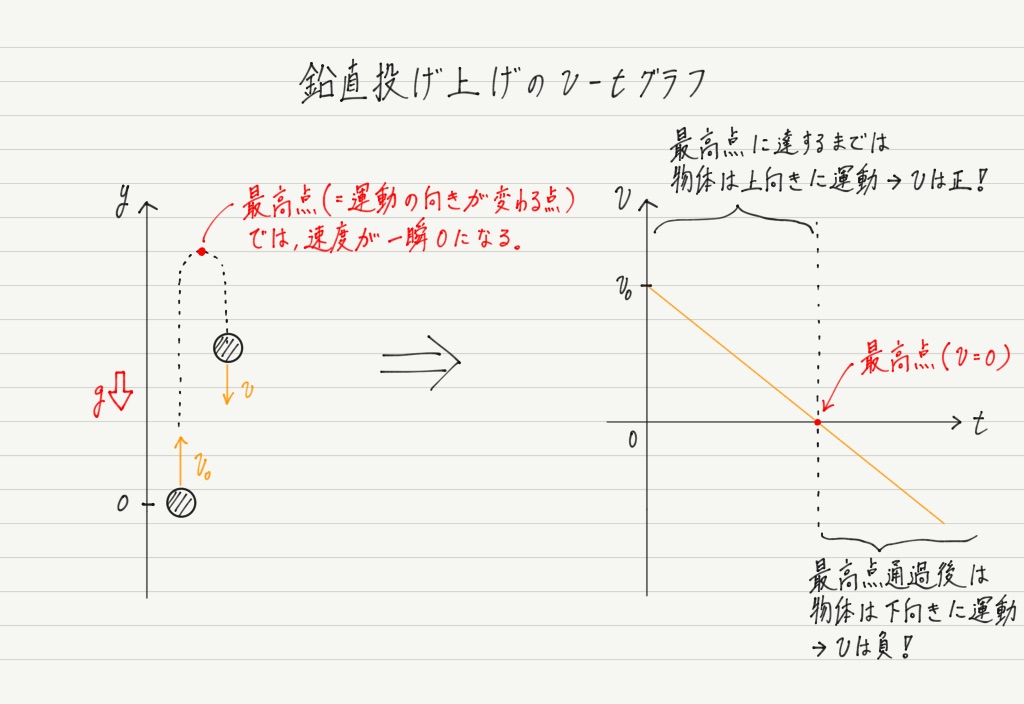
グラフについても見てみましょう。 加速度が負なので,v-tグラフは下図のようになります。
「最高点=速度が0」は問題を解くときによく使います。 暗記するのではなく,運動の様子をしっかりイメージして,最高点では(一瞬だけ)静止するということをしっかり納得してください。
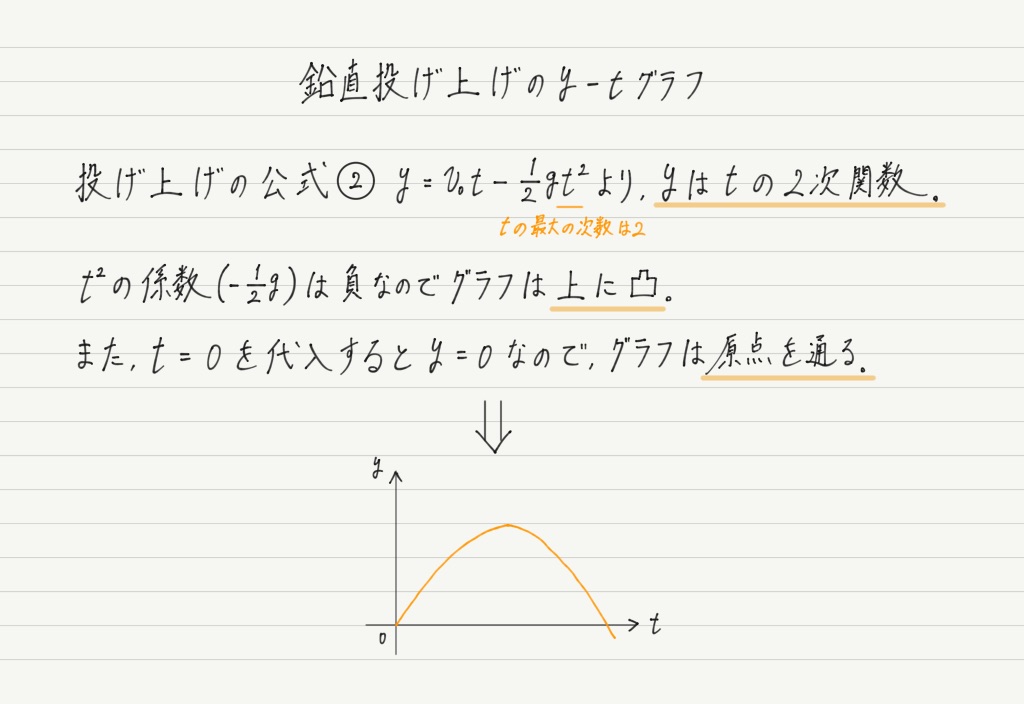
そしてy-tグラフは,投げ上げの式②より,
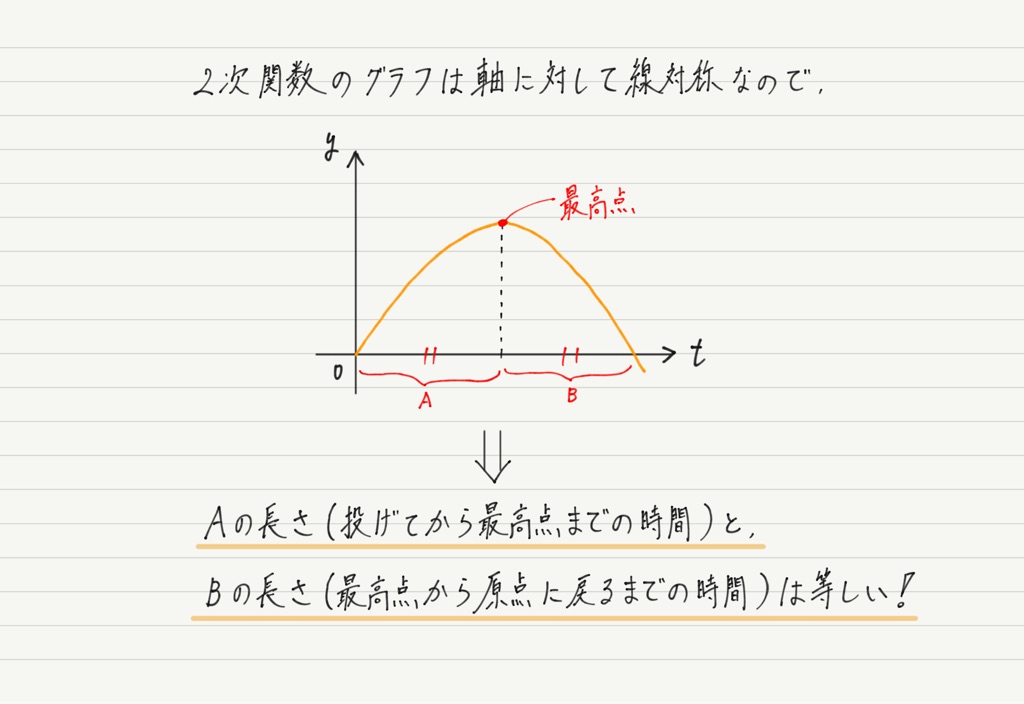
となります。 さらにここからもうひとつ,大事なことが導かれます。
この性質は「運動の対称性」と呼ばれます。 このことを知っておくと,問題を解くとき大きな助けになるのでぜひ押さえておきましょう!!
今回のまとめノート
等加速度運動はいったんここで終了。 時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。
次回予告
次回から力学の要である,力について勉強していきます。