いよいよ高校物理最初の関門,加速度運動に入っていきます!!
ここまでに学んだ具体的な運動といえば,まだ等速直線運動だけです。
等速直線運動は速さも向きも変化がない運動なので,お世辞にも面白い運動とはいえません。 そこで,等速直線運動から一歩進んで,まずは速さが変化する運動を扱おうというわけです。
等速直線運動より面白そうじゃありませんか!?
速度の変化をどう表すか
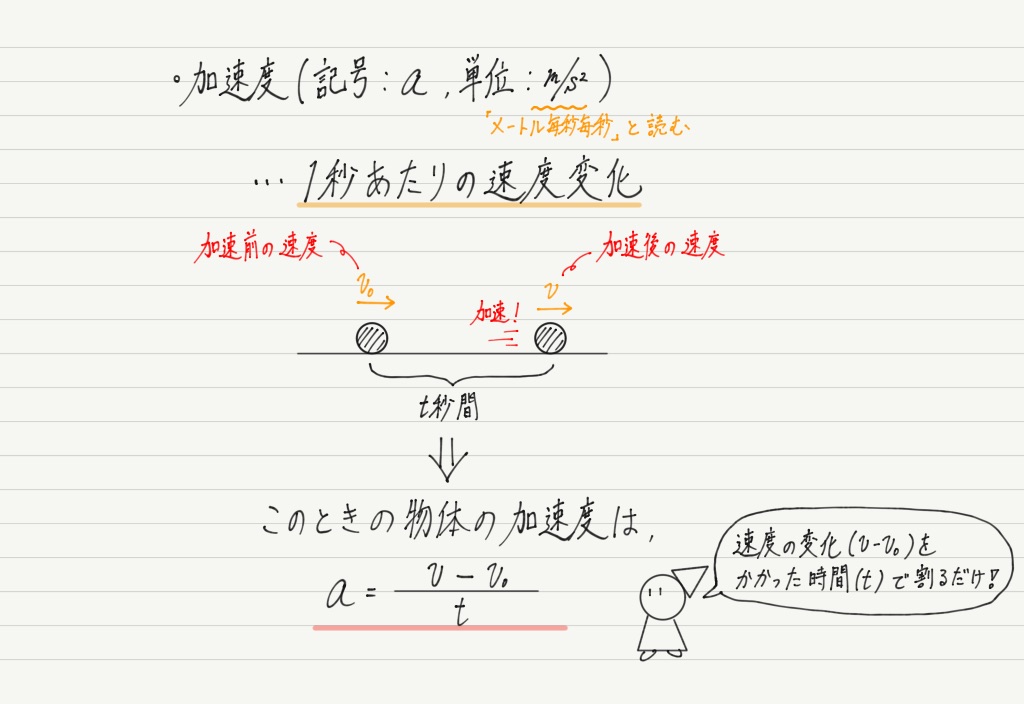
速度の変化は加速度という量で表されます。
が,単純に何m/s増えたかだけが問題ではありません。
10m/sで運動している物体が加速して50m/sになったとすると,速度変化は「40m/s増えた」ということになりますが,果たしてそれが1秒間の出来事なのか,あるいは30分間の出来事なのかで,全然話が違ってきますよね?
同じ速度変化ならば,短い時間で変化した方が「より加速した」と言えます。
そこで,加速度 = 1秒あたりの速度変化と決めましょう。
加速度の具体的な計算は,本日のまとめノートに書いておきます。
注意事項
加速度について注意点が2つほどあります。
まず1点目は,上で述べた定義の中にある単語です。 …注意深く読んでください。
1秒あたりの “速度” 変化,というところです!
“速さ”の変化ではありません!!
速さと速度の違いがあいまいな人は,以前の記事を見て確認しておきましょう。 これがわかってないと,正しく加速度を計算できません。
それから2点目。 加速度は速度と同様に向きが存在します。
加速度の向きは速度や変位と同じく,プラスやマイナスの符号で表すのですが,加速度がマイナスのときは特に注意が必要です。
負の加速度は「負の方向に加速」という現象の他に,「正の方向に減速」という現象も表します。(まとめノート参照)
どちらの意味で使われているのか,問題をよく読んで判断する必要があるので気をつけましょう。
今回のまとめノート
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。
次回予告
次回は踏ん張りどころ。 公式が目白押しです!