ここでは波の進み方の説明として用いられる「ホイヘンスの原理」について解説していきます。 ホイヘンスの原理を用いると，回折・反射・屈折という波特有の現象を統一的に説明可能！！
そんな素晴らしい（？）原理ですが，少しとっつきにくいため，補講で扱うことにしました。
学校では，ホイヘンスの原理 → 反射・屈折の法則の導出，という順序で習うこともありますが，反射・屈折の法則は導出の仕方をマスターするよりも，まずは公式として暗記して使いこなせるようにしたほうがいいです（いちいちホイヘンスの原理から導いて使ってるやつなんかいない！笑）。
それでも，「導き方も一応知っておきたい！」という人だけ読んでくださいませ。
素元波という考え方
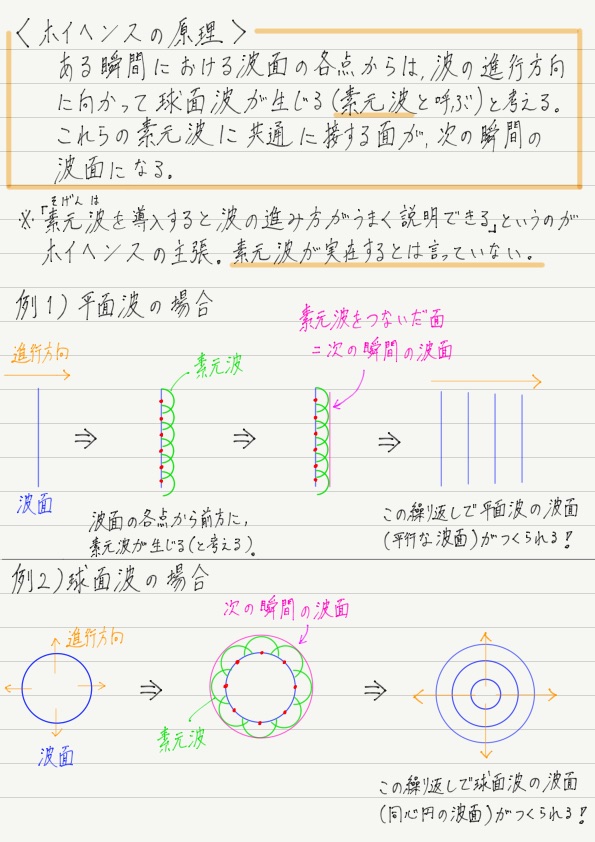
ホイヘンスの原理とは，「ある波面があったとき，その波面は次の瞬間どうなるか」を説明する原理です。 まずはその概要を見てみましょう。
（これが今回のまとめノートも兼ねています）
うーん，素元波とかいう架空の波を持ち出したりして，正直こじつけっぽい印象は拭えません笑
が，これを認めないことには始まらないので，受け入れることにしましょう（渋々）。
平面波と球面波の例だけだと，ホイヘンスの原理の何がありがたいのかよくわからないと思います。 さっそく，回折や反射，屈折にホイヘンスの原理を適用してみましょう！
回折の解釈
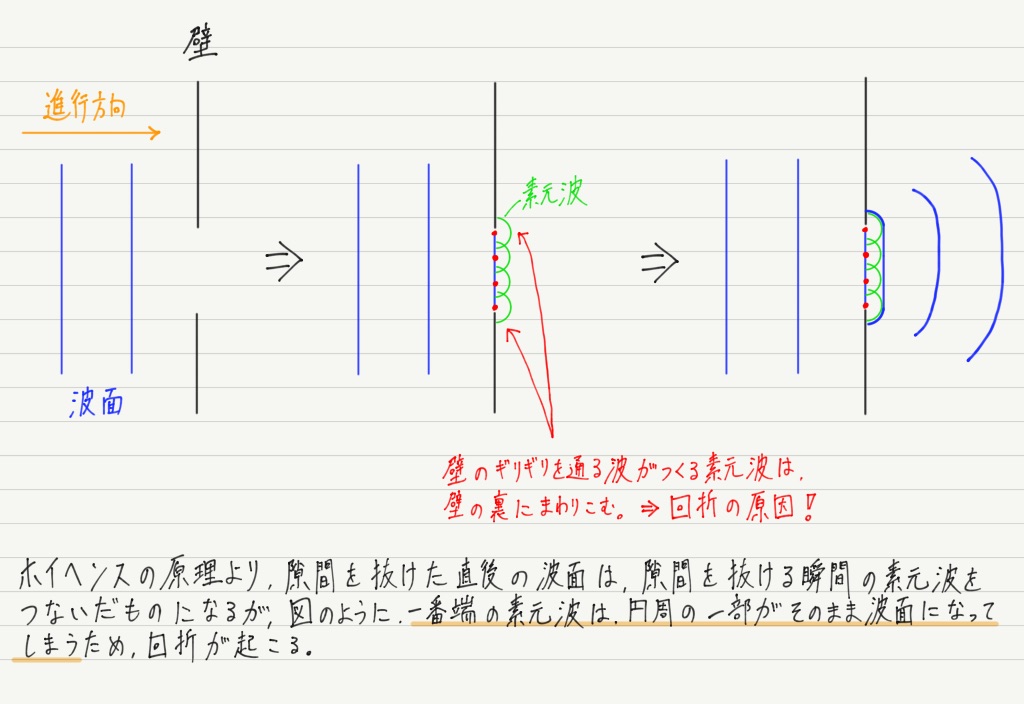
回折とは，波が障害物の裏側に回り込む現象でした。 これは普通の物体の運動ではありえないため，何とも不思議な現象に思えますが，ホイヘンスの原理を認めると…
このように素元波に着目すると，回折が起こるのはごく自然なことなのです。
反射の法則を導く
反射の法則は，「入射角と反射角は等しい」というすごくシンプルな法則です。
当たり前にも思える法則ですが，ちゃんと証明しろと言われたらどうしますか？ なかなか難しそうじゃないですか？
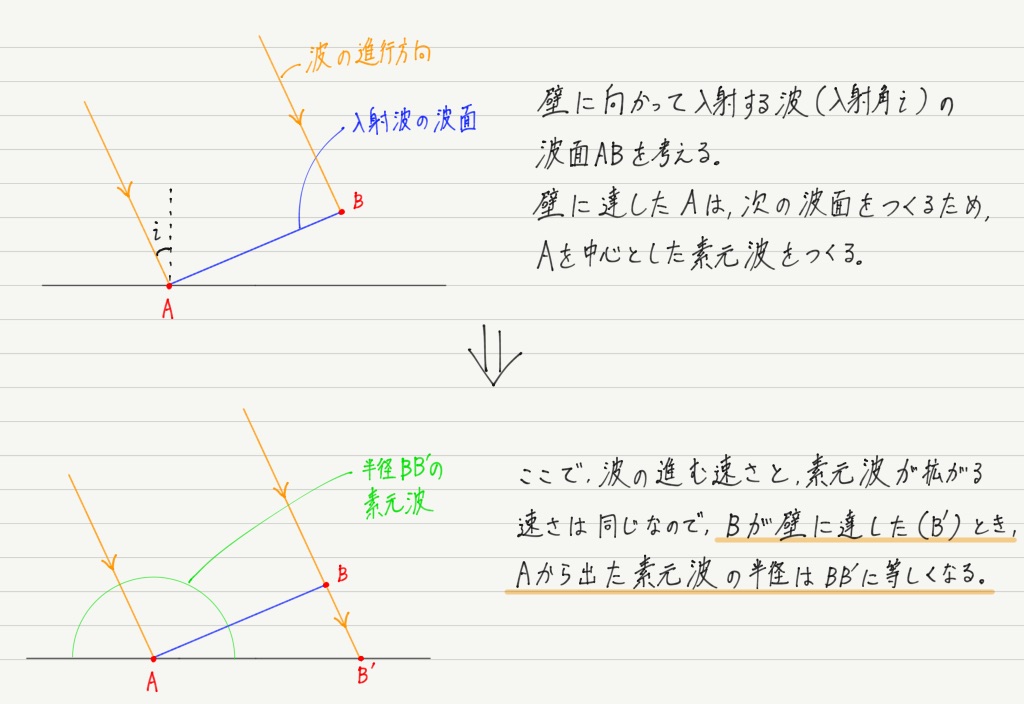
でもご安心ください。 ホイヘンスの原理にお任せあれ。
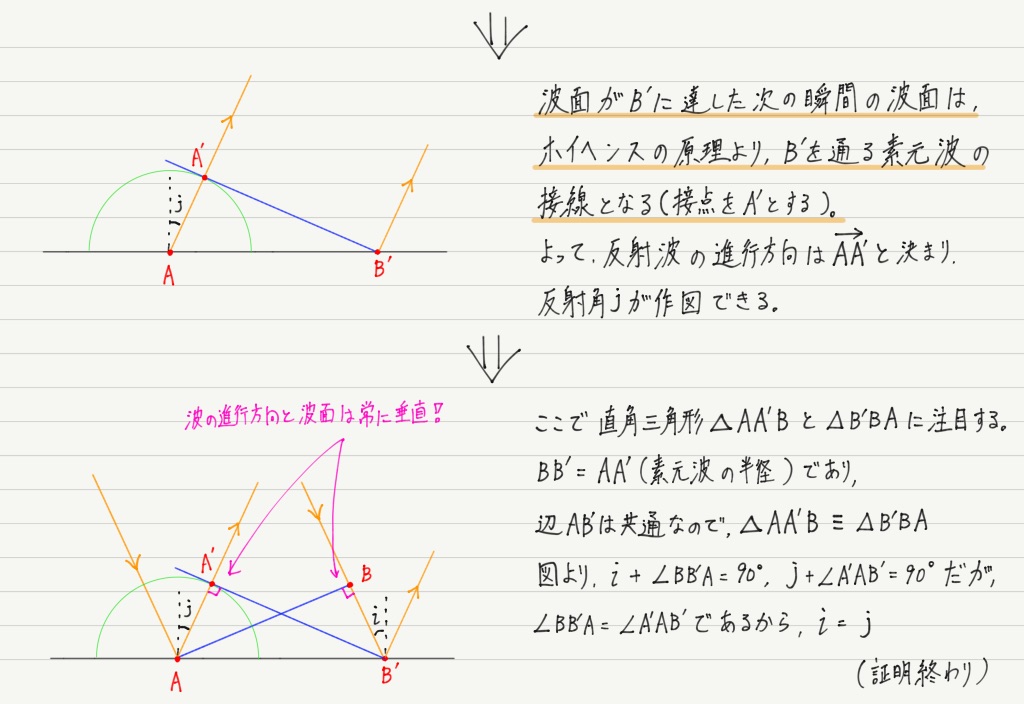
ほら，証明できた！ 証明のポイントは素元波の半径。 波面の作図でも，計算でも，素元波を書く場合は必ず半径に注意してください。
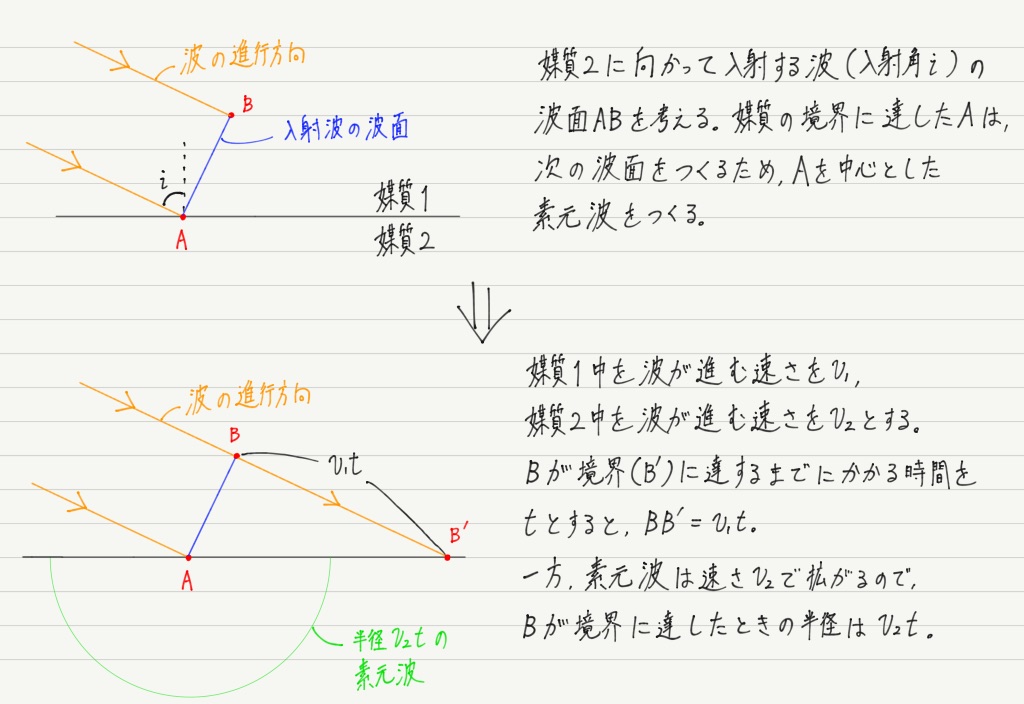
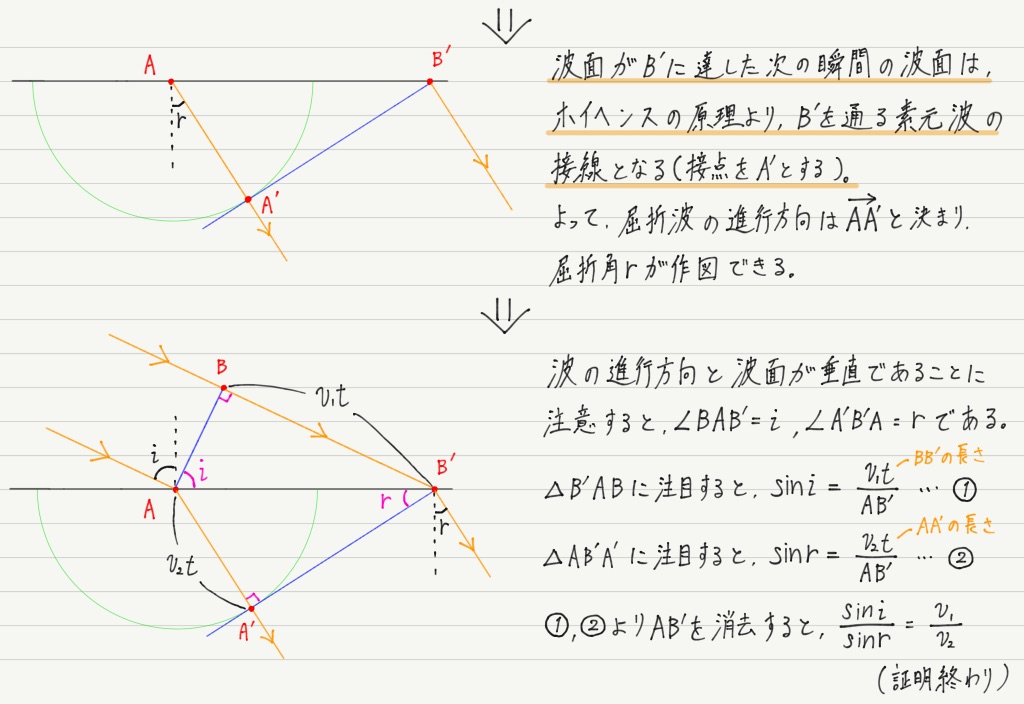
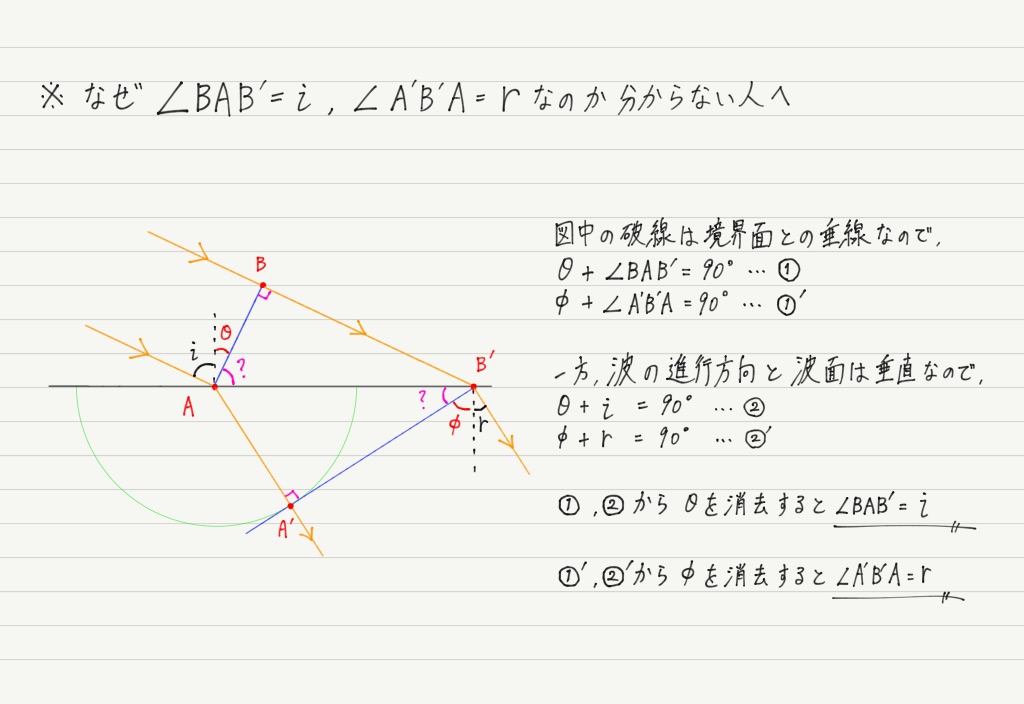
屈折の法則を導く
屈折の法則も導いてみましょう。 こちらも素元波の半径に注意です！
図さえちゃんと描ければ，計算は簡単ですね♪
冒頭でも書いた通り，反射の法則や屈折の法則は覚えて使えることが大事。
ホイヘンスの原理はおまけ程度に理解しておいてもらえればと思いますが，演習問題を用意したので，理解の助けにしてください。
