小学校の算数の時間を思い出しましょう!
「Aさんは12時に家を出て,家から800m離れた郵便局に向かったところ,12時10分に着きました。Aさんの歩く速さは分速何mですか。」
こんな問題をたくさん解いたことと思います。計算は簡単ですね。
Aさんの速さ = 800m ÷ 10分 = 80m/分になります。
平均という考え方
さっきの問題の答え,よく考えるとちょっとおかしくないですか?
人が移動するとき,ずーっと同じ速さというのは考えにくいですよね?
現実的に考えれば,郵便局に行く途中に信号で止まったり,疲れたからゆっくり歩いたり,速さは変化するのが自然です(屁理屈? いや,現実はそうですよね)。
それなのに上の計算ではそういうことを一切考慮せず,単純に「全体の移動距離」と「かかった時間」だけで速さを求めています。
つまりこれは,Aさんが「一定の速さで歩いていたとしたら,分速80mである」ということを言っているに過ぎません。 これを物理では「平均の速さ」と呼びます(さらに向きがついていれば,平均の速度です)。
80m/分で歩いているからといって,1分ごとに本当に80mずつ進んでいるわけではありません。 これが平均 という考え方。
しかし物理では,「一定の速さだとしたら」という仮定の話ではなく,「実際に速さがどう変化したのか」が大事になってきます。
それには「12時5分のときのAさんの速さ」,「12時6分のときのAさんの速さ」というように,より正確な「瞬間の速さ」(くどいですが,向きがついていれば瞬間の速度)の情報が必要です!
では,瞬間の速さ(または瞬間の速度)はどのようにして求めればよいでしょうか?
“瞬間” を求めるにはどうすべきか
平均の速さの問題点は,速さを求めるのに用いる時間が長すぎるということです。 さっきの問題では10分間でしたが,そりゃ10分もあれば途中で速さが変化して当然です。
そこで,瞬間の速さを求めるときには,時間間隔を短くします!!
例えば,12時5分のときの瞬間の速さを知りたかったら,12時5分から12時5分1秒の間に進んだ距離を用いて速さを出す,といった具合。
「12時5分から12時5分1秒の間の速さ」はこれはもう,「12時5分での速さ」と言ってほぼ差し支えないでしょう。
1秒ではまだ長いというならもっと短くすればOK。 1秒より0.1秒,0.1秒より0.01秒,… と,時間間隔は短ければ短いほど,瞬間の速さはより正確になります。 これだけ短いと速さが変化する隙がないですもんね。
まとめると,平均の速さと瞬間の速さのちがいは,「速さ = 距離 ÷ 時間」の「時間」が長いか短いかのちがいです。 計算の仕方が変わるわけではないので安心してくださいね!
グラフで見る平均と瞬間のちがい
平均の速度と瞬間の速度のちがいをグラフで確認しましょう!
速度はx-tグラフの傾きで表されるのでした。
ひとつ補足しておくと,xが移動距離ならば傾きは必ず正になるので,傾きは「速さ」を表しているといえます。
一方,xが変位ならば傾きは負にもなりえます。 マイナスは向きを表していて,この場合の傾きは速さではなく「速度」を表しています(今後断りがなければ,xは変位を表すものとします)。
話を戻しましょう。 物体の運動が等速でない場合は,x-tグラフは直線のグラフになりません。
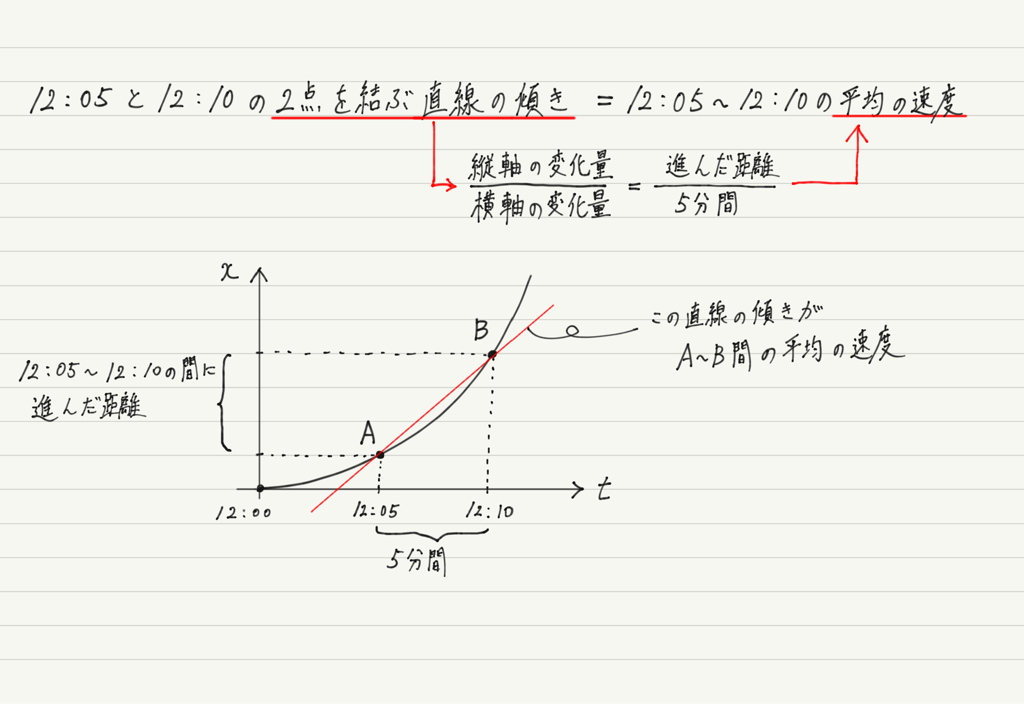
この場合,平均の速度は下図のようにしてグラフから求められます。
次に,点Aでの瞬間の速度をグラフから読み取る方法を考えてみましょう。
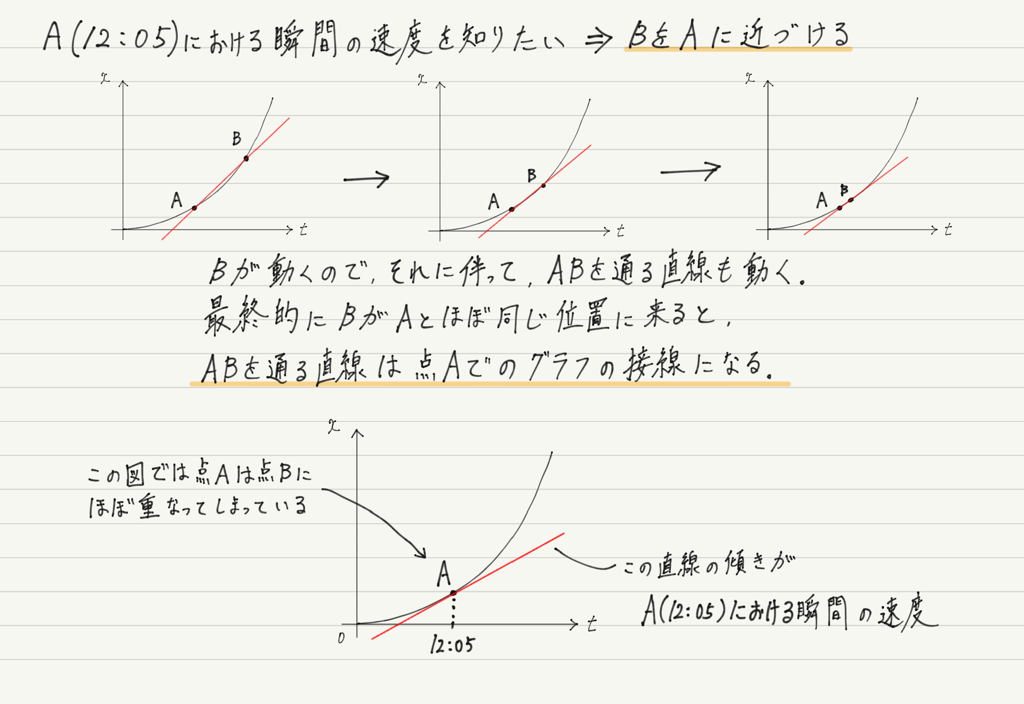
瞬間の速度を求めるにはAとBの時間間隔を短くすればいいので,図の点Bをグラフに沿ってどんどんAに近づけていきます。
AとBを通る直線が,点Aでの接線に近づいていく様子がイメージできましたか?
このように,ある時刻における瞬間の速度は,x-tグラフの「その時刻における接線の傾き」として表されます!
加速度の場合
加速度にも「平均の加速度」と「瞬間の加速度」が存在します。
これは難しい話ではなくて,いまやった平均の速度と瞬間の速度の話をそっくりそのまま加速度に替えただけ。
つまり,「加速度 = 速度変化 ÷ 時間」の「時間」が長ければ平均の加速度,短ければ瞬間の加速度になります。
また,加速度が変化する運動では,ある時刻とある時刻の間の平均の加速度は,v-tグラフでその2点を結んだ直線の傾き,ある時刻での瞬間の加速度は,v-tグラフのその時刻での接線の傾きになります。
今回のまとめノート
ちなみに,物理ではあまり平均の速度や平均の加速度は扱いません。
よって,単に「速度」や「加速度」と書かれている場合,特に断りがなければ,瞬間のほうを指していると解釈してください!
時間に余裕がある人は,ぜひ問題演習にもチャレンジしましょう。