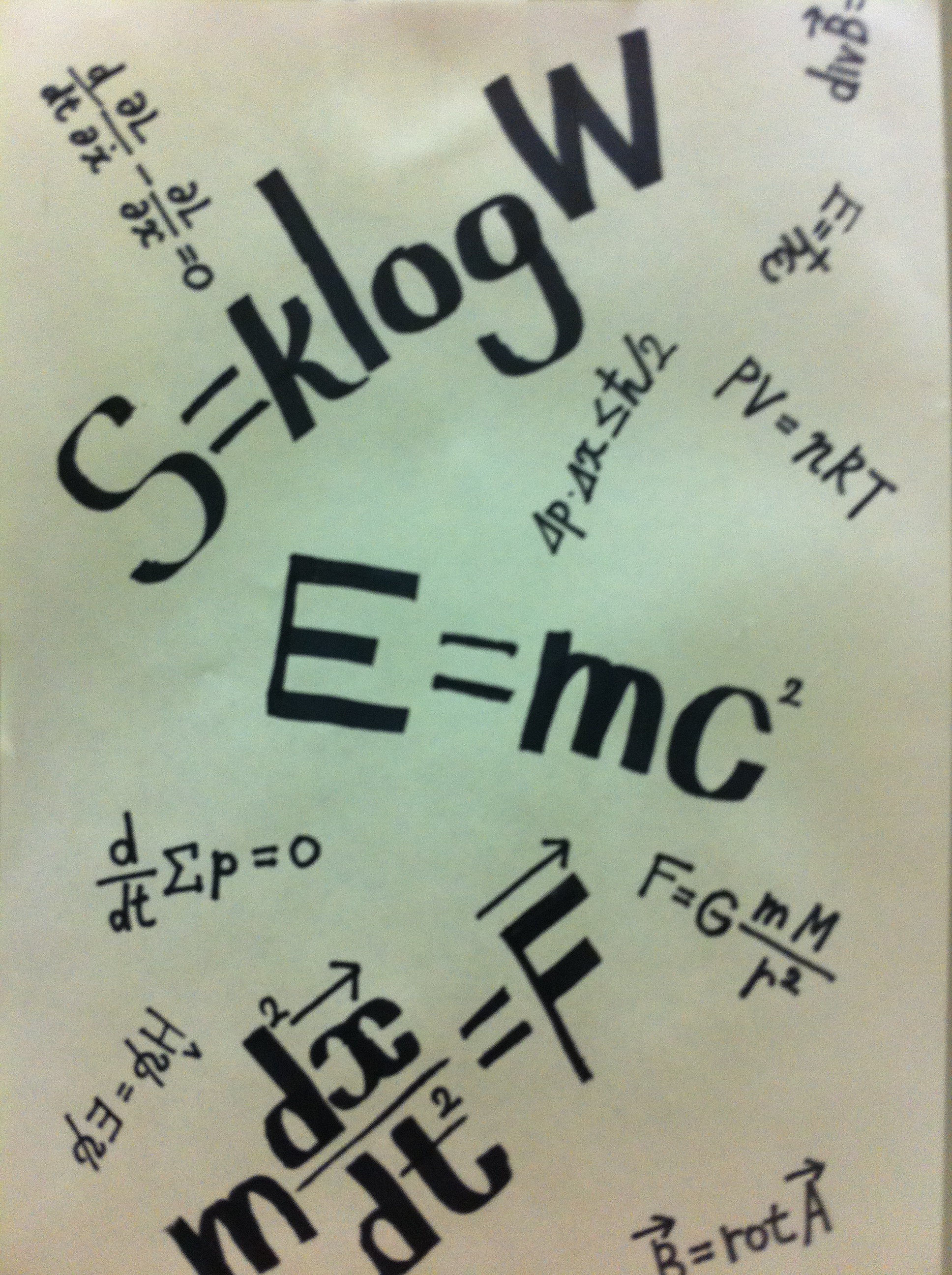Elastic Potential Energy

When you hear the term “potential energy,” the first thing that comes to mind is “energy possessed by an object at a high place”.
However, potential energy is a much broader term, and the potential energy of an object at a high altitude is only one of them.
This lecture, let’s study another kind of potential energy, which is not gravitational potential energy.

Work done by spring

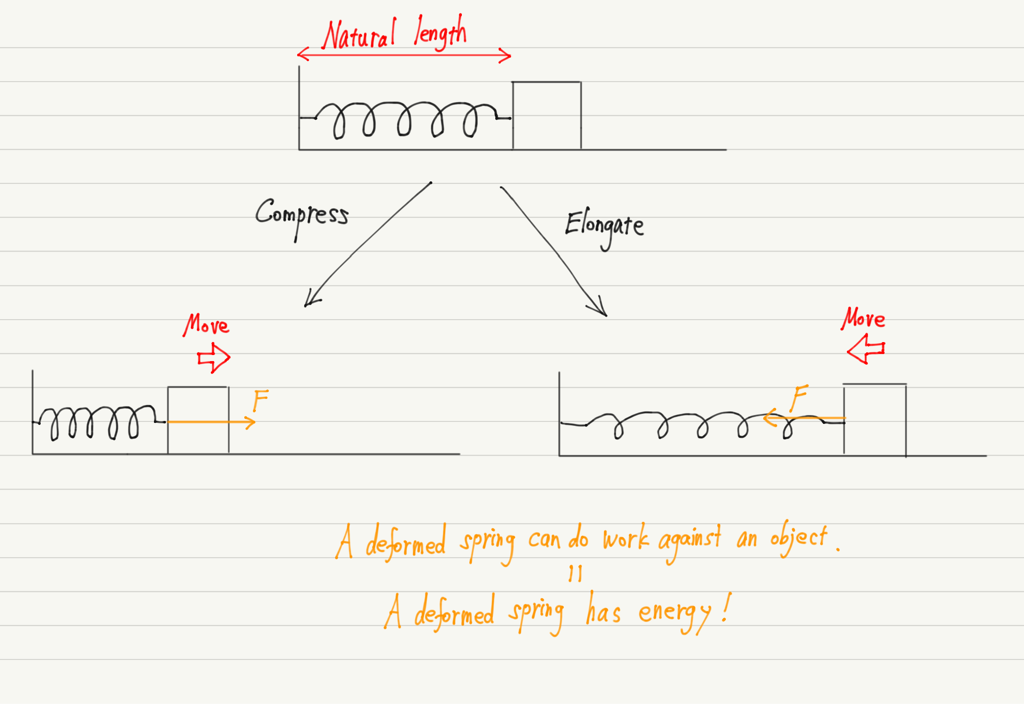
When a spring is deformed, it exerts a force to return to its natural length, and this force can do work on the object.

Being able to do work means that a deformed spring has energy!
Of course, if the spring is not deformed, the energy is zero (the energy reference point is at the spring’s natural length).

When a spring is deformed even slightly from its undeformed state, it has energy as it tries to return to its natural length. Isn’t this similar to gravity?

Gravity also has zero potential energy with respect to the ground, since an object cannot fall any further when it is on the ground.
However, if it is lifted even slightly off the ground, it will have potential energy as it tries to fall to the ground.

At the beginning of this article, I wrote that there are multiple types of potential energy, but potential energy is a general term for the energy that an object possesses when it shifts its position from the reference and starts moving on its own when you release your hand.

In the case of a spring, the elastic force causes the spring to return to its natural length, so the energy possessed by the spring is also called potential energy.

Are there other potential energies?

By the way, if you are asking if there is other potential energy besides gravitational and elastic force, the answer is yes.
What other potential energies are possible?

Forces with positional energy have one thing in common.
If you remember what you learned before, you can answer the question.
Those who have forgotten should reread the following article.

Related articles

Conservative Force

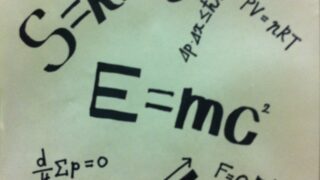
Gravitational and elastic force were classified as conservative forces.
In fact, it is known that if a force is a conservative force, the potential energy of that force can always be calculated.
This means that, sooner or later, potential energy will make its way into electromagnetism!

How to calculate potential energy

As was the case with gravitational force, potential energy is “the work done by the force from the point of displacement to the point of return to the reference point”.
Based on this, let us find the potential energy of the elastic force.

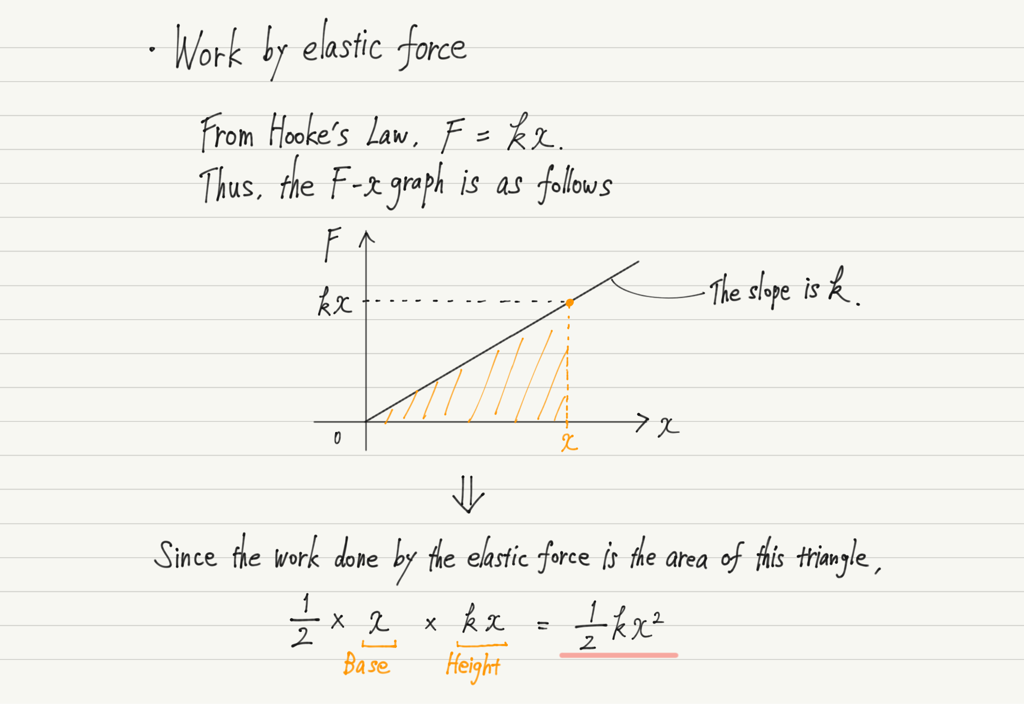
The elastic force when deformed x [m] from its natural length is kx [N] from Hooke’s law.
The work done to return to the natural length is force × distance, so kx²?

Actually, this calculation is incorrect. Can you point out where it is incorrect?

The answer is that the formula for work cannot be used because the elastic force is not constant during the return to its natural length.

In the case of gravitational force, the magnitude mg was constant regardless of height, but since the elastic force is proportional to the amount of deformation x, the closer to the natural length, the smaller the elastic force.
And the formula “Work = force × distance” can only be used if the force is always constant while moving.

So, is work not required when forces change?

No, it is not too early to give up. If you can’t find it by calculation, consider using a graph.
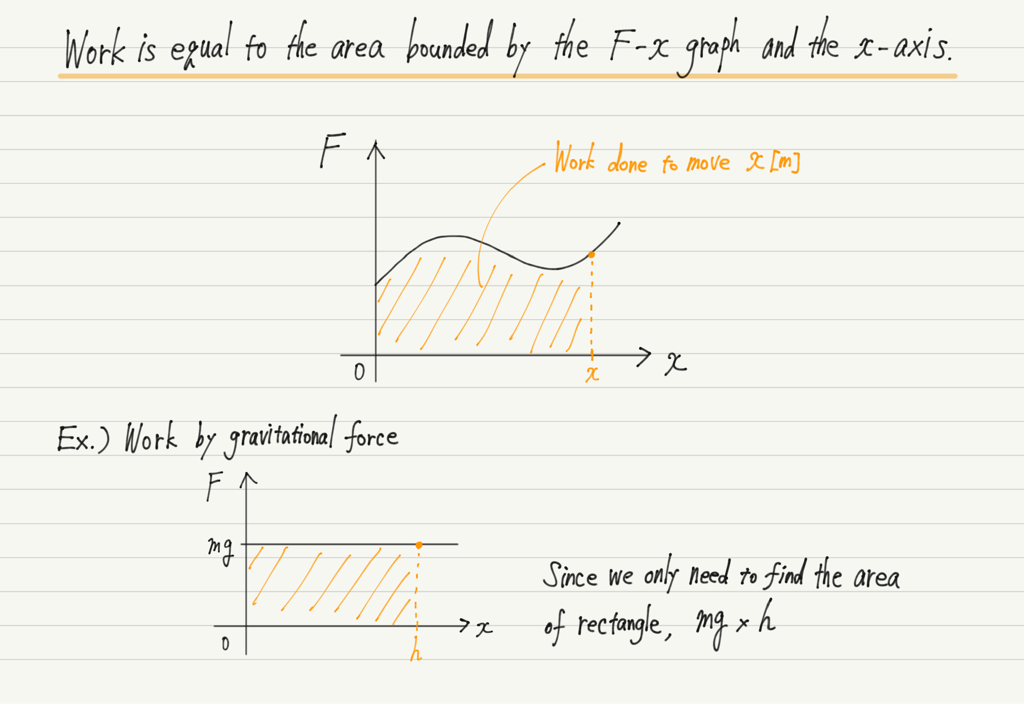
In fact, we know that the work done by a force is equal to the area enclosed by the F-x graph and the x-axis.

Using this fact, we find the work done by the elastic force.

This is the formula for elastic potential energy!

Notes on calculation

Two points should be noted about the elastic potential energy.

The first point. In the case of gravitational force, we were promised that we could freely determine the criterion of potential energy, but in the case of a spring, we are not free to do so.
The reference point in any case is the natural length of the spring.

Second point. In the case of gravitational force, the sign of the potential energy changed depending on whether the object was above or below the reference point.
However, elastic potential energy is always positive whether the spring is elongated or compressed.  Make no mistake!

Summary of this lecture

Next Time

Now that we have kinetic and potential energy out of the way, next time we will discuss the law of conservation of mechanical energy, which is essential to solving mechanics problems!

Related articles

Law of Conservation of Mechanical Energy