Average and Instantaneous

Let’s try a simple math problem.

Mr. X leaves his house at 9:00 a.m. for the post office 800 meters from his house and arrives at 9:10 a.m.
How fast is Mr. X walking in meters per minute?

The answer, of course, is 800 m ÷ 10 min = 80 m/min.

The concept of Average

Isn’t the answer to the previous question a little strange when you think about it?
It is hard to imagine that people move at the same speed all the time, isn’t it?
Realistically speaking, it is natural for the speed to vary, such as stopping at a traffic light on the way to the post office, or walking slowly because one is tired.

Nevertheless, the above calculation ignores all of these factors and simply calculates the velocity based on the “total distance traveled” and the “elapsed time”.

So this just means that if Mr. X were walking at a constant speed, he would be walking at 80 m/min.
This is called “average velocity” in physics.

Just because you are walking at 80 m/min does not mean that you are really advancing 80 meters every minute.
This is the concept of average.

In physics, however, it is not a matter of hypothetical “if it were a constant speed”, but rather “how the speed actually changed”.
That would require more precise “instantaneous velocity” information, like “Mr. X’s speed at 9:05”!

Then, how can we find the instantaneous velocity?

How to obtain instantaneous velocity

The problem with average velocity is that the time used to find the speed is too long.
In the previous problem, the time period was 10 minutes, but it is natural that the speed changes during the 10 minutes.

So, when we find the instantaneous velocity, we shorten the time interval!

For example, if you want to know the instantaneous velocity at 12:05, you can use the distance traveled between 12:05 and 12:05:01 to determine the velocity.

The “velocity between 12:05 and 12:05:01″ is now almost safe to say that this is “the velocity at 12:05”.

If 1 second is still too long, then make it shorter.
The shorter the time interval, the more accurate the instantaneous velocity will be: 0.1 second instead of 1 second, 0.01 second instead of 0.1 second, and so on.

In summary, the difference between the average velocity and the instantaneous velocity is the difference between a long time and a short time.
The calculation method does not change, so don’t worry!

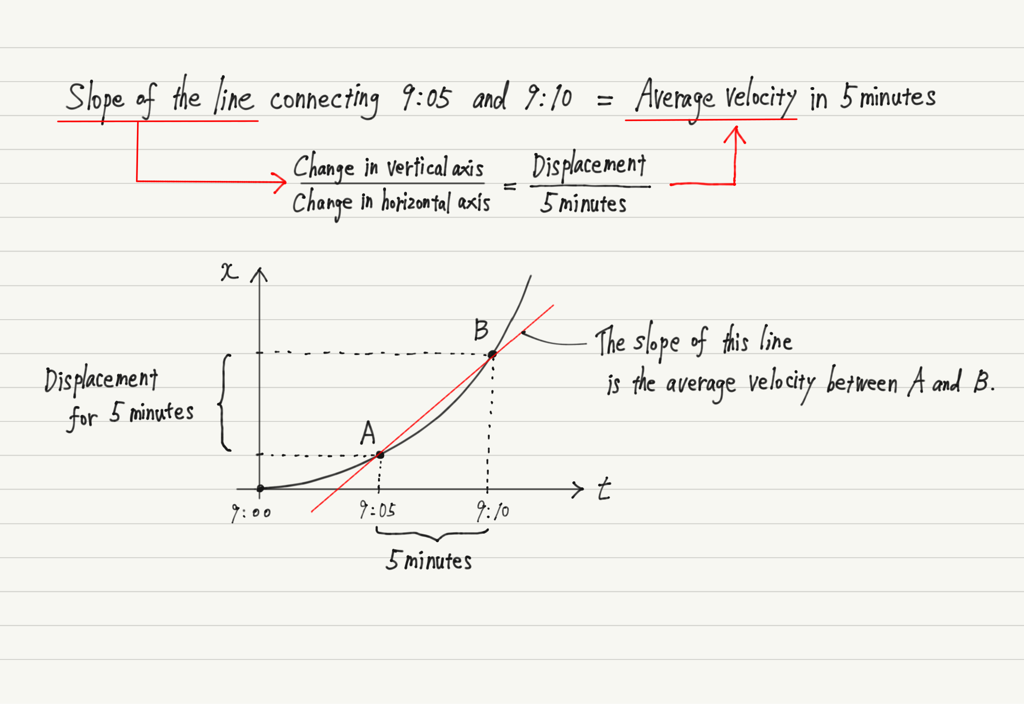
Difference between average and instantaneous in graphs

Check out the difference between the average velocity and the instantaneous velocity on the graph!

Velocity was represented by the slope of the x-t graph.

Related articles

Graph of Uniform Linear Motion

Now, if the motion of an object is not constant velocity, the x-t graph will not be a straight line graph.
In this case, the average velocity is obtained from the graph as shown below.

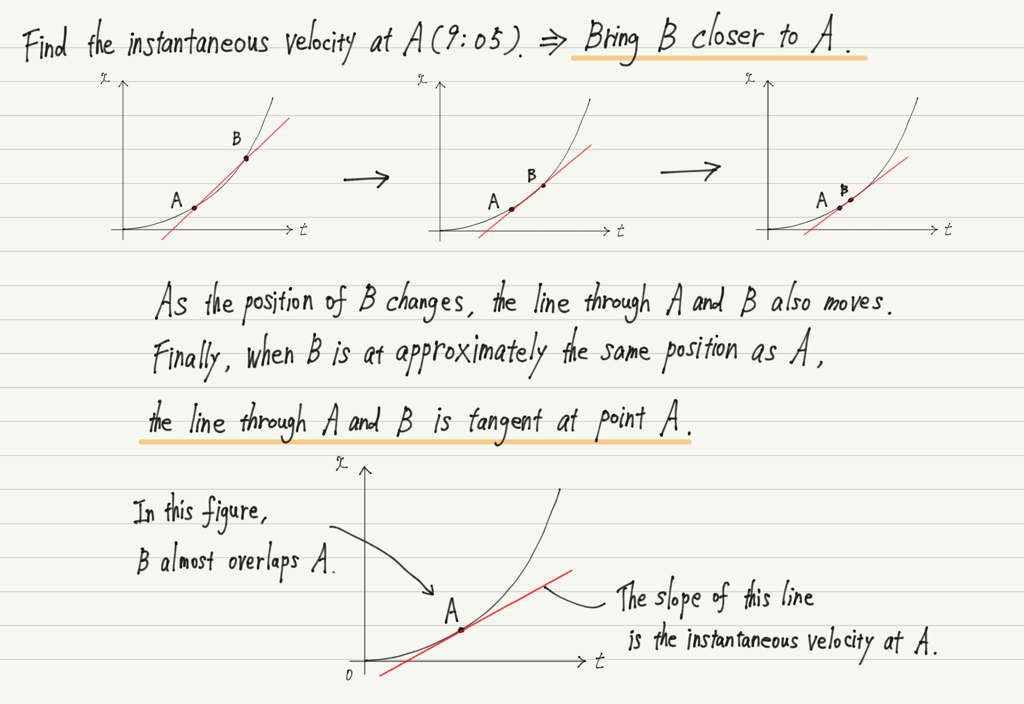
Next, let us find the instantaneous velocity at point A.

To find the instantaneous velocity, we can shorten the time interval between A and B, so we move point B in the figure closer and closer to A along the graph.

Did you picture the line passing through A and B approaching the tangent line at point A?

Thus, the instantaneous velocity at a given time is expressed as “the slope of the tangent line at that time” of the x-t graph!

In case of acceleration

There are “average acceleration” and “instantaneous acceleration” in acceleration.
This is not a difficult matter; it is just a matter of replacing the discussion of average velocity and instantaneous velocity with acceleration.

In other words, if the time of “acceleration = change in velocity ÷ time” is long, the acceleration is the average acceleration, and if it is short, it is the instantaneous acceleration.

For motions with varying acceleration, the average acceleration is the slope of the line connecting the two points on the v-t graph, and the instantaneous acceleration is the slope of the tangent line on the v-t graph.

Summary of this lecture

Incidentally, physics does not often deal with average velocity or average acceleration.
Therefore, if you see simply “velocity” or “acceleration,” unless otherwise noted, interpret it as referring to the instantaneous one!