気体の3つの状態量P,V,Tのうち,Pが一定の変化(定圧変化)とVが一定の変化(定積変化)については考察が終わったので,今回は残る1つ,等温変化(Tが一定の変化)について見ていくことにしましょう!
温度が一定 = 内部エネルギーが変化しない
温度が一定といえばボイルの法則をすでに習っていますが,前回までと同様に熱力学第1法則に絞って考えていくことにします。
さて今回はQ, ⊿U,Wのどれに注目すればいいでしょう?
正解は⊿U。
内部エネルギーについては数回前の記事で扱ったばかりなので覚えててほしいところですが,忘れている人はLet’s 復習!
温度と内部エネルギーが直接関係しているということは常に意識しておいてください。
温度の変化がないということは内部エネルギーの変化もないわけで,これを式で表すと,⊿U=0ですよね!
等温変化と熱力学第1法則
等温変化 → ⊿U=0ということがわかったので,これを熱力学第1法則に代入すると…
Q=0+W
という関係式が得られます。
等温変化では,加えた熱はすべて仕事に使われるということを示しており,人間でいうと食べたカロリーの分だけ仕事をして消費するという理想的な状態です。
「熱を加える」と聞くとどうしても温度が上昇すると連想してしまいがちですが,熱を加えることと温度が上がることはまったく別物ということを,この等温変化は教えてくれています。
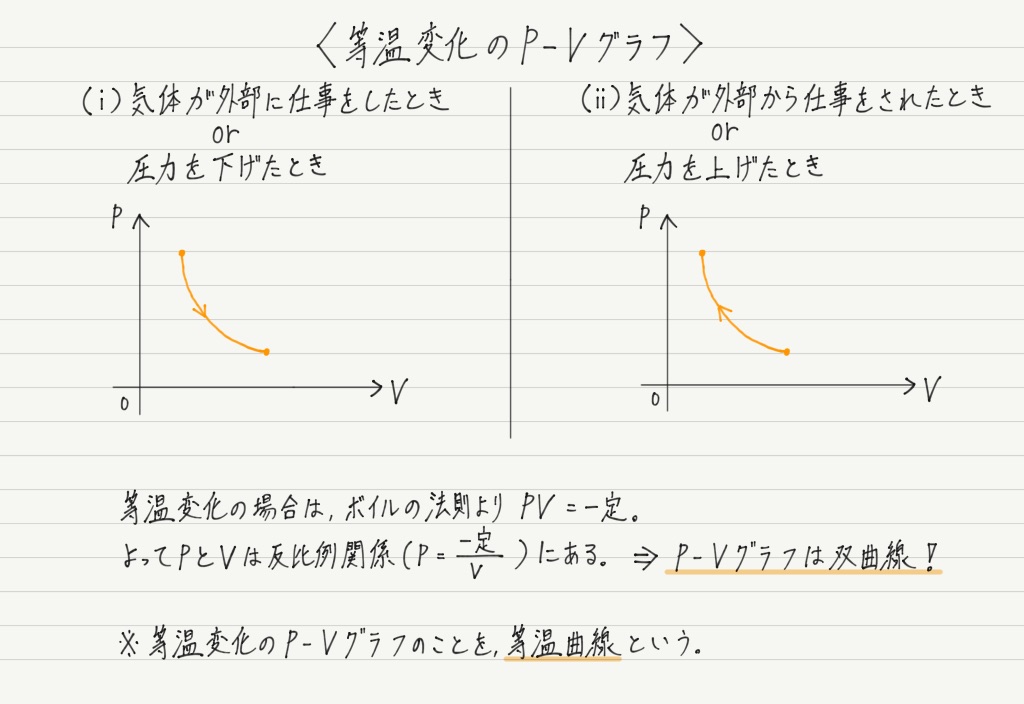
等温変化のP-Vグラフ
ここで等温変化のP-Vグラフも見ておきましょう。
定積変化や定圧変化は軸に平行なグラフになって面白味に欠けるのですが,等温変化はいくぶん様子が異なります。
気体の温度を一定にしたまま圧力や体積を変えると, 上図のように等温曲線に沿って状態が変化します。
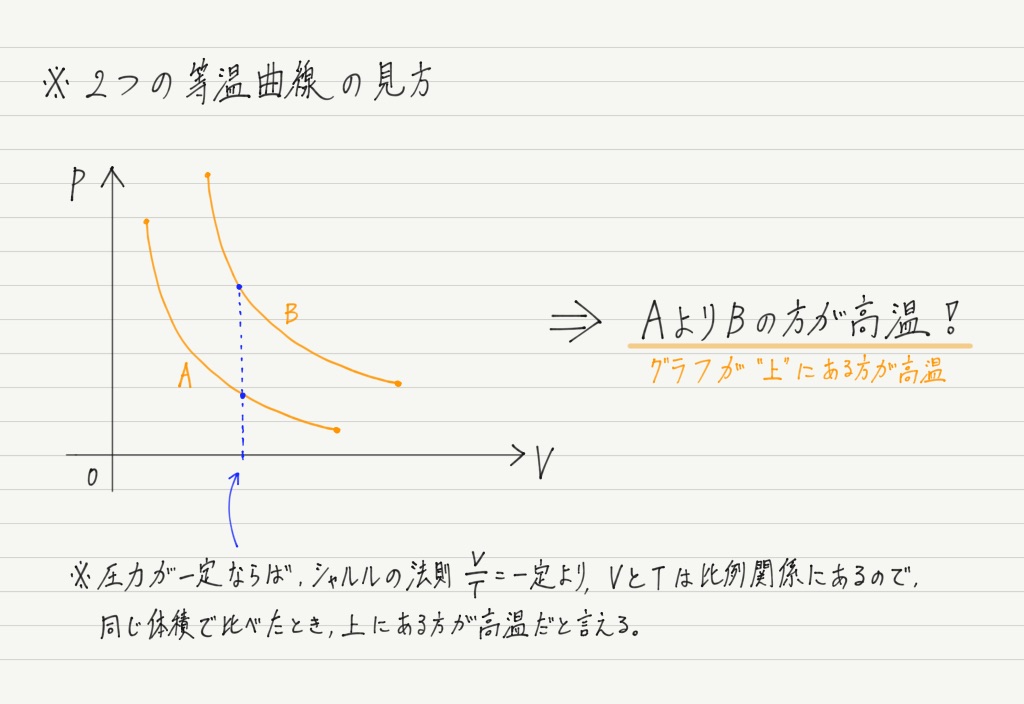
ところで,問題によっては等温曲線が2つ与えられる場合もあります。
その場合は2つの等温曲線の位置関係に注目してください。
このことがわかっていれば,等温曲線はバッチリ。
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。
次回予告
1つの状態量が一定の変化についてはこれで全パターン網羅しました!
が,実はまだ大事な状態変化が残っているのです。