物理の学習では計算をする場面が非常に多いです。
これは物理学という学問の性質上しかたのないことですが,計算をするにあたって気をつけなければいけない点も多々あります。
数学の小難しいルールのことを言っているのではありません。
なんと,足し算ひとつとっても注意すべき点があるのです!
1+1が2にならない!?!?
「向き」の重要性
早速ですが,こんな問題を考えましょう。
この問題,(1)は1m+1m=2mでOKですが,(2)は1N+1N=2Nとはなりません!
確かに1Nの力が2つはたらいていますが,お互い逆を向いているため力が打ち消しあってしまいます。
よって(2)の答えは0Nが正解。
1と1を足したのに0になってしまうのです。
こんな変なことが起こった原因は,力に “向き” があるから。
(2)の2つの1Nは同じ1Nではなくて,「右向きに1N」と,「左向きに1N」と区別すべきもの。
一方,(1)の2つの1mは同じ1mです。 棒の長さに向きなんてありません。
ここで用語を紹介します。
力のように向きをもつ物理量のことをベクトル,長さのように向きをもたない物理量のことをスカラーと呼びます。
物理ではこの2種類を区別することが非常に重要。
いま見た足し算の例だけでも,その重要性はわかってもらえると思います。
以下ではそれぞれについて詳しく見ていきましょう。
ベクトル
まずはベクトルから。
先ほどは力を例にとって説明しましたが,向きをもつ物理量は他にもたくさんあります!
【高校物理で登場するベクトルの例】
力・速度・加速度・変位・運動量・電場・磁場・etc…
これらはすべて1+1=2になるとは限らないので,計算するときは要注意。
「…なぁ,さっきからそればっかり言ってるけど,実際に足し算するときはどうしたらいいの?」
そんな疑問にも丁寧に答えるのがこのサイトのスタイル。
ベクトルの基礎をかいつまんで説明します!
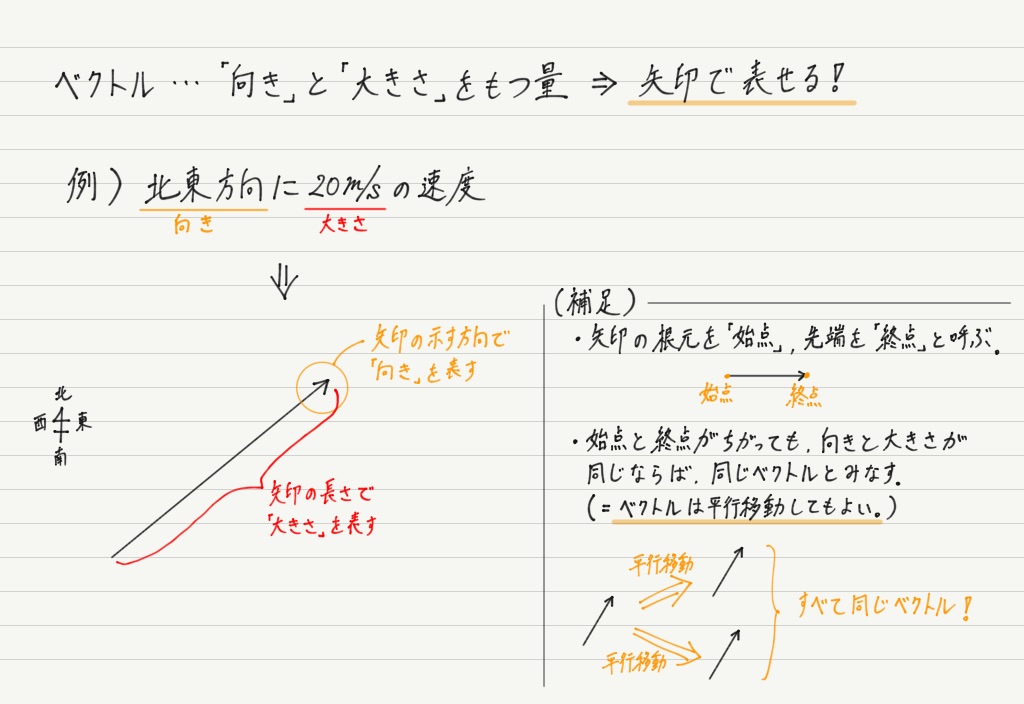
細かいことはゴチャゴチャ言わずに,とりあえずベクトル=矢印のことだと思ってください。
では,いよいよベクトルの足し算の説明をしていきます。
ベクトルを足すときには,大きさどうしを足すのではなく,“矢印として” 足すことになります。
この例題で「ベクトルの和」と「長さの和」が一致するのは(1)のような特別な場合だけ。
(2)〜(4)を見れば,ベクトルの足し算は大きさを足すだけではダメ,ということがよく分かりますね!
ベクトルは足し算だけではなく,引き算も重要です。
以上のような,“矢印としての計算” ができるようになれば第1段階クリア。
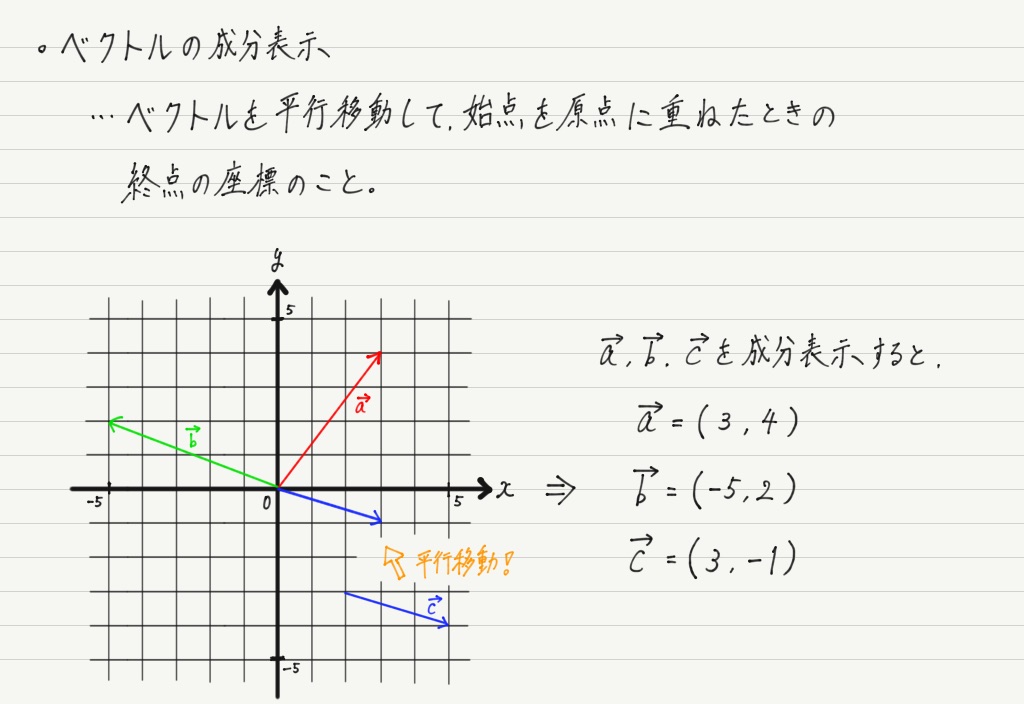
ただせっかくなので,ベクトルの計算において非常に強力な手段となる「成分表示」についても学んでおきましょう!
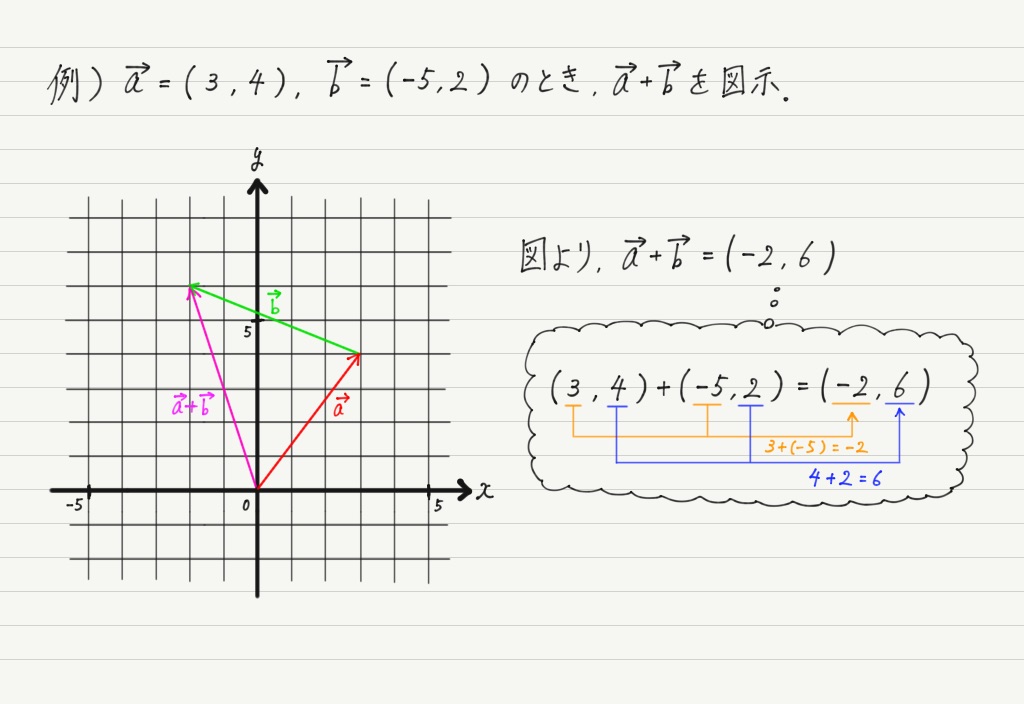
さっき学んだベクトルの足し算を,座標の上で行ってみましょう。 すると…
なんと,x成分どうし,y成分どうしを足したものになっています!
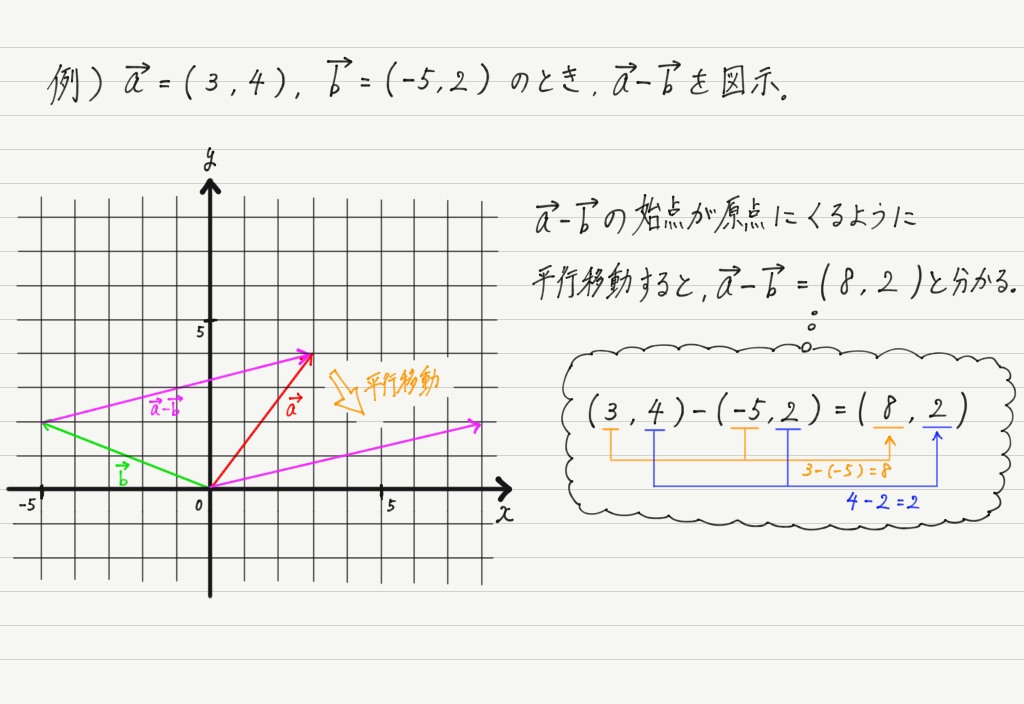
引き算も同様。
ベクトルは大きさをそのまま足したり引いたりすることはできないけれども,成分表示で考えれば,成分ごとに足し算・引き算が可能。
これはつまりベクトルの成分だけ教えてくれれば,わざわざ作図しなくてもベクトルの和や差が計算できちゃうってこと。
これってめちゃくちゃ便利じゃない!?
物理の問題では実際にどう使うのかが知りたい!という人は,こちら↓の記事を参照してください。
まだまだ奥が深いベクトルの世界ですが,高校物理をやるだけならこれぐらいのことを知っておけばOK。
これ以上の解説はどこかの数学サイトにおまかせします。
スカラー
向きが重要な役目をもつ物理量がある一方で,向きをもたない量(スカラー)も存在します。
【高校物理で登場するスカラーの例】
質量・速さ・距離・仕事・エネルギー・温度・電位・etc…
これらは向きがないため,計算においてはただの数値と思ってOK。
公式に数値として代入して普通に計算。 楽チン!
ただし! スカラーはただの数値として計算していいとはいえ,むやみに足したり引いたりしてはいけません。
最初の問題で,1m+1m=2mという計算をしました。
これは長さがスカラーだからそのまま足し算できたわけですが,同じスカラーである温度はどうでしょう?
1℃の水と1℃の水を混ぜたら2℃?
もちろんそんなことにはなりませんね!
1℃の水と1℃の水を混ぜても,もちろん温度は1℃のままです。
スカラーだからといって何でもかんでも自由自在に足したり引いたりできるということはありません。
「スカラーはベクトルとちがって簡単だなー」なんて思ってると足をすくわれますよ?
以上,ベクトルとスカラーに関する基本知識でした!
教科書・参考書を読むときや問題を解くとき,物理量がベクトルなのかスカラーなのかをしっかり意識することを心がけましょう。
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。