物体の運動を語る上で外せないのが変位と速度,それから加速度です。
単振動においてもこれらが重要であることは言うまでもありません。
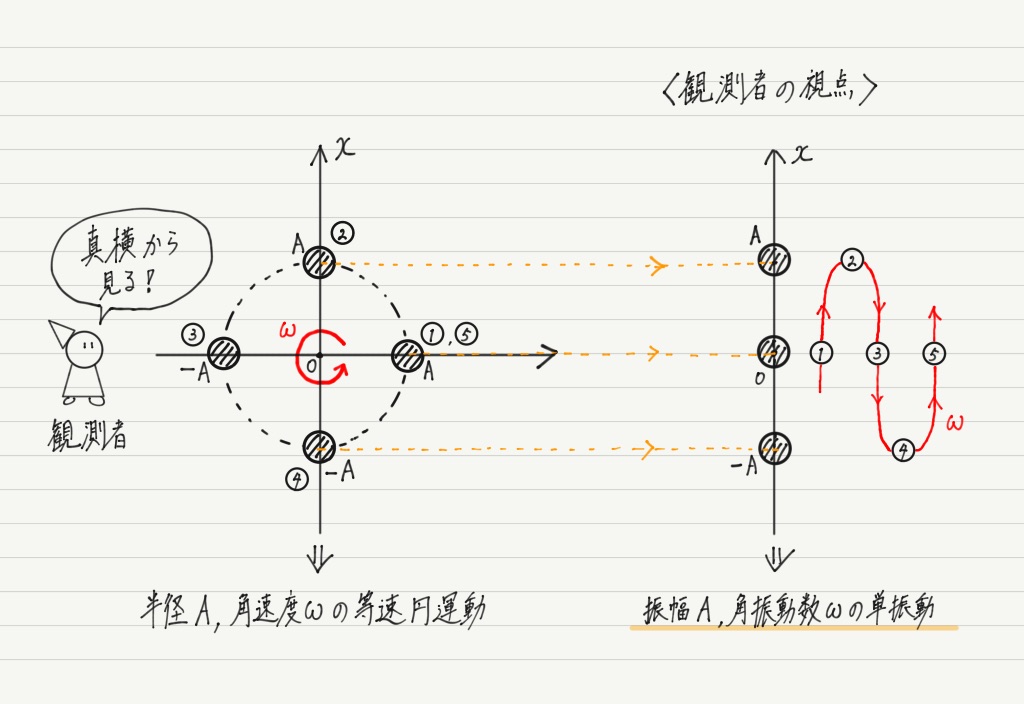
等速円運動をヒントにして,これらの量を求めてみましょう!
① 変位
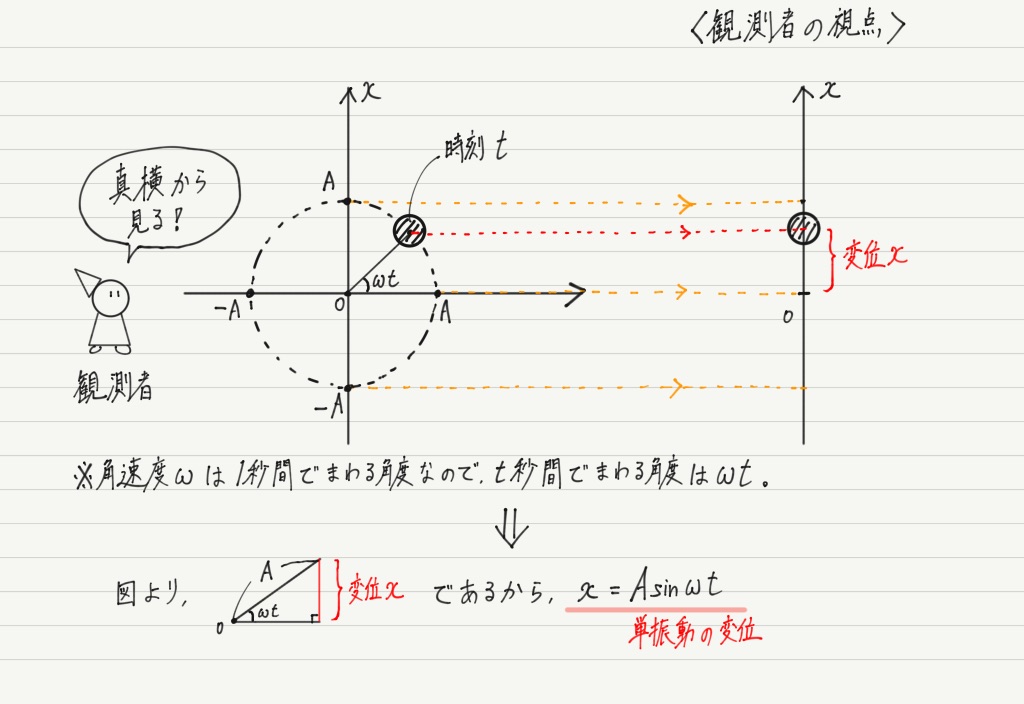
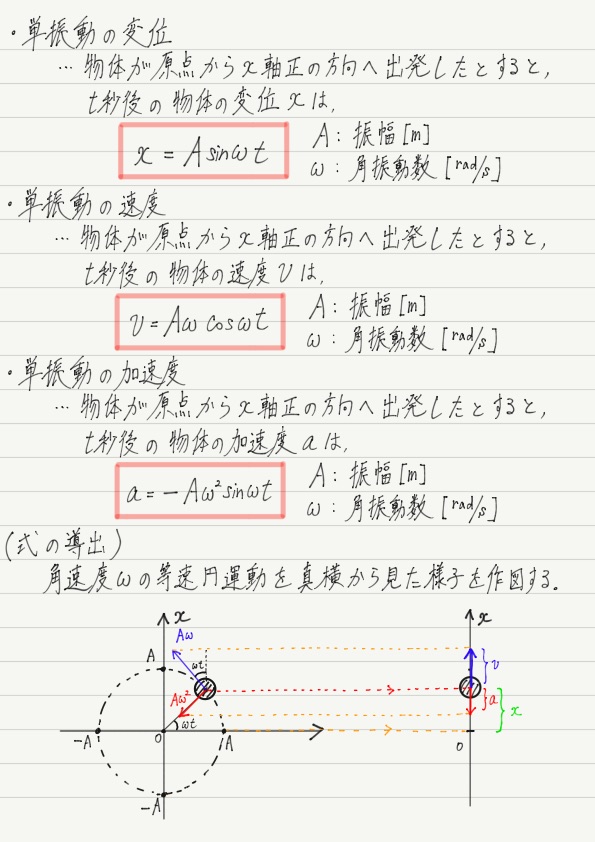
今回はオーソドックスに時刻 t = 0で振動の中心(x = 0)からx軸正方向にスタートする単振動を考え,時刻 t における物体の変位を求めてみます。
前回の復習になりますが,この運動は,物体が半径Aの円周上を点(A , 0)から反時計回りにまわる等速円運動を真横から見たものとまったく同じです!
これをヒントに単振動の変位を導いてみましょう。
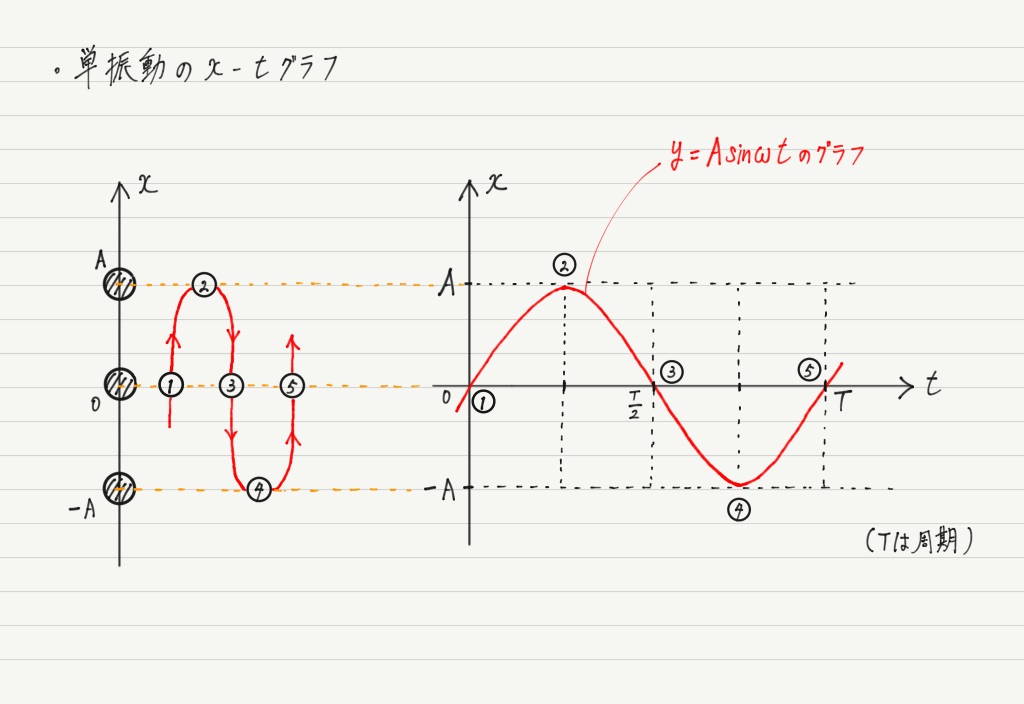
これをもとにグラフを書いてみると…
単振動する物体の変位は時間の経過とともに,正弦波を描いて変化することがわかりました。
これは意外な結果ではなく,予想通りですね。
この話は波の分野とも密接に関連しています。
② 速度
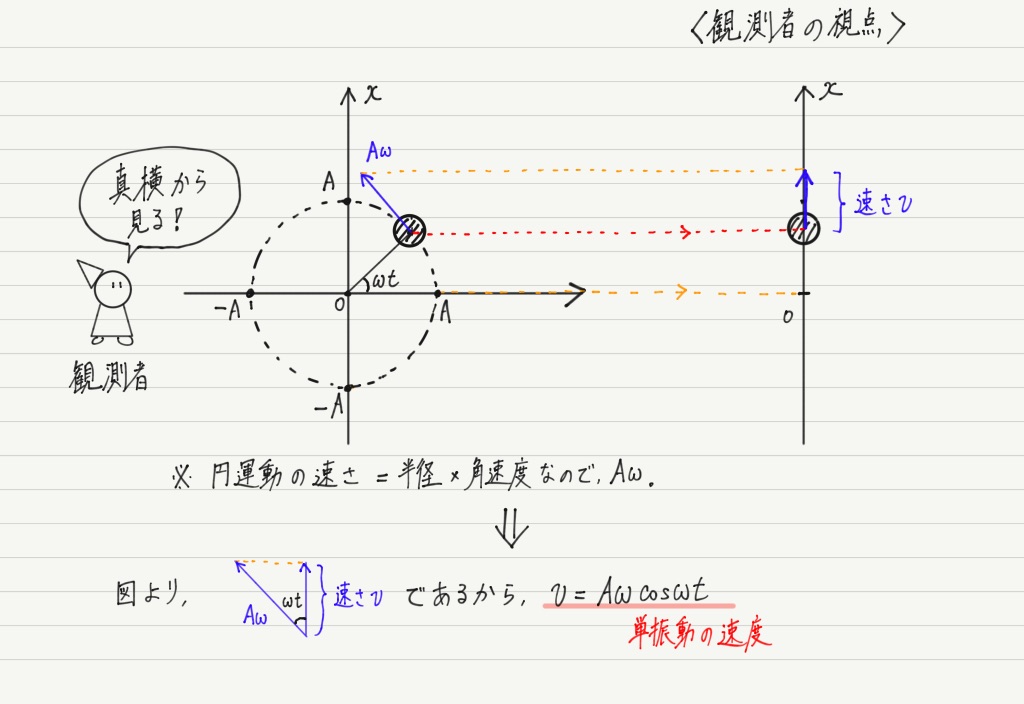
次に速度。
時刻 t における単振動の速度は,時刻 t における円運動の速度(円の接線方向)を真横から見たものなので…
簡単!
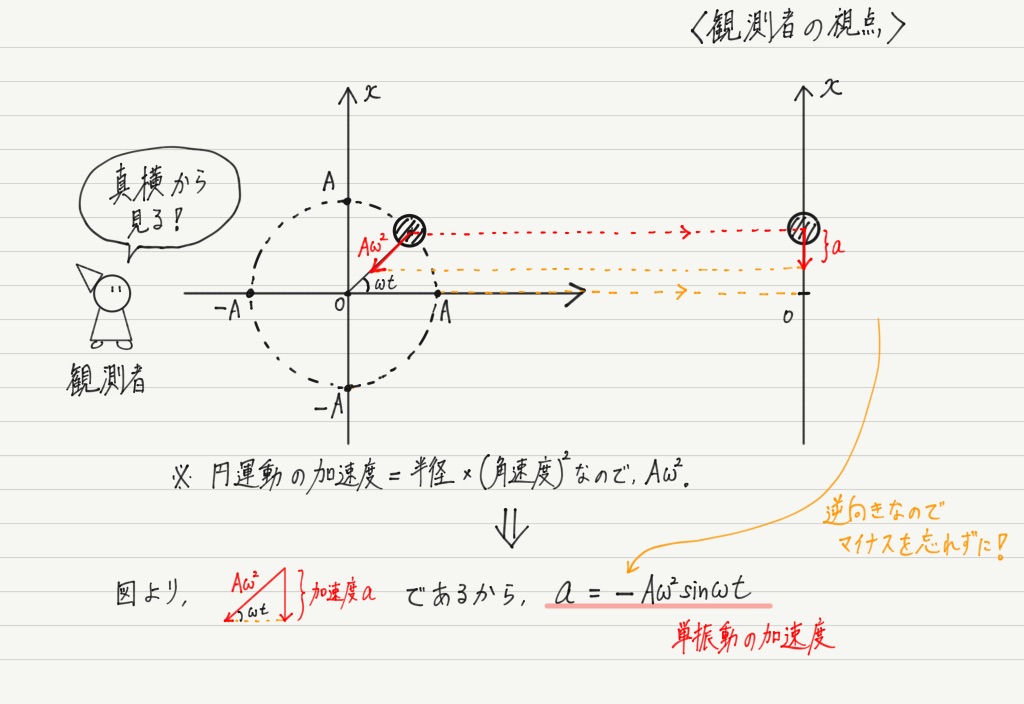
③ 加速度
最後に加速度ですが,同様に円運動を真横から眺めればそれでOK。
円運動の加速度は中心へ向かう向きだったので…
これで本日の内容はおしまい。
変位・速度・加速度は重要!といいつつ,三角形の辺の長さを求めただけなので拍子抜けだったかな?
図を描けば簡単に求められる今回の結果ですが,いちいち図を書くのは大変なので覚えておいたほうがいいのではないかと思います。
今回のまとめノート
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。
【余談】
知ってる人も多いかと思いますが,単振動の速度と加速度はもっと簡単な方法で求めることが可能です。
ただし,その “簡単な方法” は機械的すぎて,「求めることはできるけどその計算の意味はわからない」となってしまいがちです。
私としては最初は「単振動=等速円運動を横から見たもの」と理解してほしいので,あえて図形を用いました。
とはいえ,“簡単な方法” にまったく触れないわけにもいかないので,それはまた別の機会に説明したいと思います。
次回予告
今回,単振動の加速度を求めることができました。 ということは次はもちろん…