本来であれば運動方程式は「物体にはたらく力を用いて加速度を求める」ためのものですが,単振動に関しては力の話題に触れることなく,先に加速度が求められてしまいました。
本来の順序とは逆ですが,加速度がわかったのならこれを使わない手はありません。
加速度を用いて単振動する物体にはたらく力を求めてみましょう!
単振動する物体にはたらく力
ではさっそく,前回求めた加速度を運動方程式に代入して…
と言いたいところですが,そのままだとsinが入ってきて面倒なのでちょっと策を弄してみましょう。
加速度がスッキリした形で表せました!
ではこれを運動方程式に代入してみます。
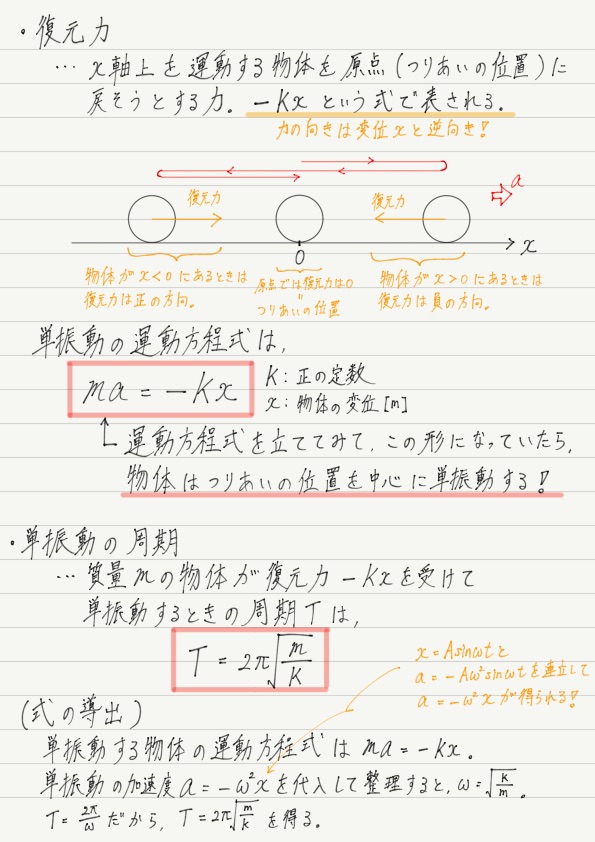
この計算で,「単振動している物体には −Kx (Kは正の定数)と表される力がはたらく」ということが導かれましたが,その逆,「物体にはたらく力が −Kx の形ならば,その物体は単振動をする」も成り立ちます。
いつものように物体にはたらく力を書き,加速度の向きを決め,運動方程式を立ててみて,もし ma = −Kx という形になっていたら,「あ,この物体は単振動をするんだ」と気付けるようになってください!!
これは重要な事実なのでしっかり押さえておきましょう。
復元力の向きと大きさ
上で求めた力の式を吟味してみましょう。
式を見て得られる情報は,
・マイナスがついていること(力の向きに関する特徴)
・変位 xに比例していること(力の大きさに関する特徴)
の2点です。
まずは向きについて。
マイナスがついているので「逆向き」を表すわけですが,これは当然,xに対して逆向きということを表しています。
ただし,「x軸と逆向き」ではなく,「変位 xと逆向き」という意味です!!
ここは勘違いしないように!
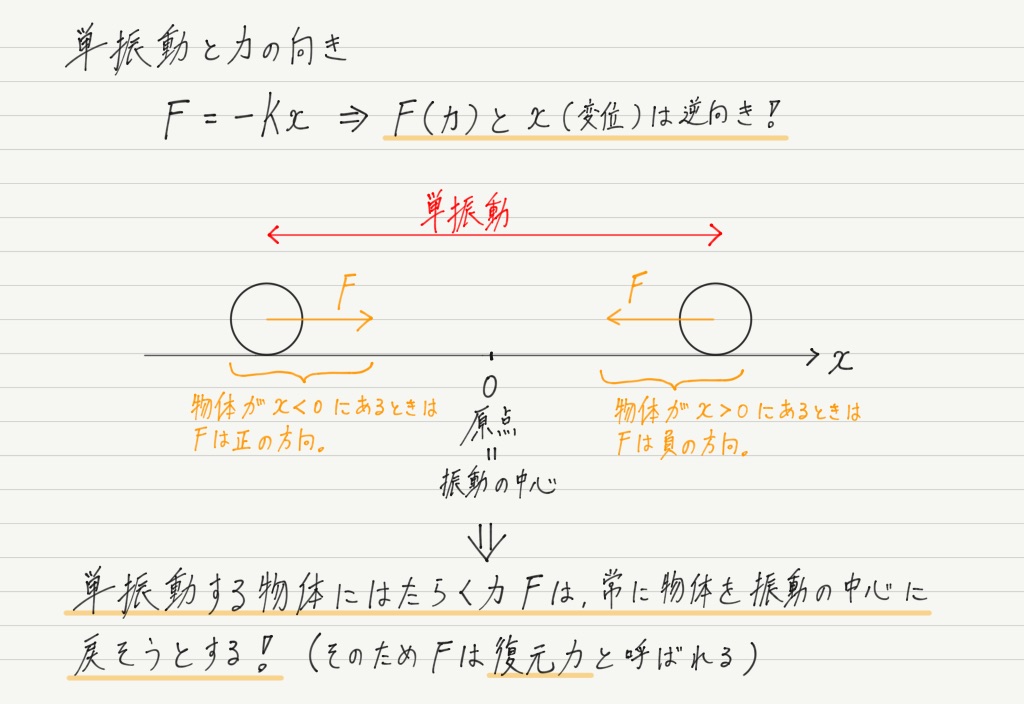
物体の位置によって向きが変わるというのが復元力の最大のポイント!
次に復元力の大きさですが,変位 xに比例するので「原点から遠くに行くほど,より強い力で引き戻される」ということになります。
要するに一定の大きさではないということ(大きさが一定だったら単振動ではなく等加速度運動になってしまう!)。
そして当たり前ですが,物体が振動の中心(x = 0)にあるとき,F = 0となります。
「力が0」という意味を込めて,振動の中心は「つりあいの位置」とも呼ばれるので覚えておきましょう。
結局,復元力というのは「向きも大きさも一定ではない」という,高校物理にしてはなかなか厄介な力です。
こうなると,「復元力を求める→運動方程式に代入→運動方程式を解く(=加速度を求める)」という王道の流れは断念するしかなく(大学物理レベル!),高校の教科書では「加速度がわかった→運動方程式に代入→復元力を求める」という形にならざるを得ないわけです。
そんな事情なので定期試験や入試において,単振動の運動方程式を “立てる” ことはあっても,“解く” ことはありません。
それでも,ma = −Kxという形の運動方程式を見かけたら,「これは単振動だ!」と気付けるようにはしておきましょう!
(大事なので2回目!)
単振動の周期
そんな大人の事情もわかったところで(笑),最後に単振動の周期を求めてみましょう。
この周期の式は公式として覚えてください!
ただし,実際にこの式を使って周期を求めるには復元力の比例定数Kが必要。
世の中にはいろいろな単振動がありますが,その都度物体にはたらく力を見つけて計算し,Kに相当する部分を求める必要があります。
単振動の運動方程式は解かないけど,やはり物体にはたらく力は重要ということですね〜
今回のまとめノート
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。
次回予告
具体的な単振動の例題を解きながら,理解を深めていきましょう!