等速円運動は中心方向には加速度をもちますが,等速なので接線方向の加速度は0です。
しかし,等速でない円運動ならば接線方向にも加速度をもちます。
今回は振り子を例に用いて,接線方向の運動方程式を考えてみましょう!
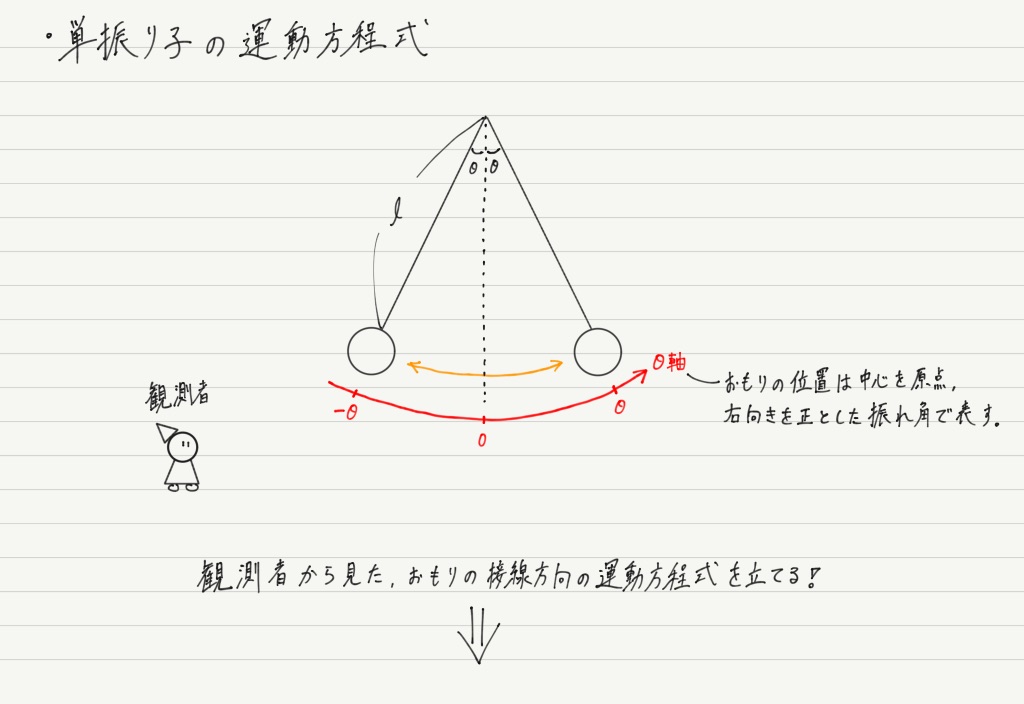
単振り子の運動方程式
いわゆる “普通の振り子” のことを,物理では単振り子と呼んでいます。
さっそくですが,単振り子を外から見ている観測者の立場で運動方程式を立ててみましょう!
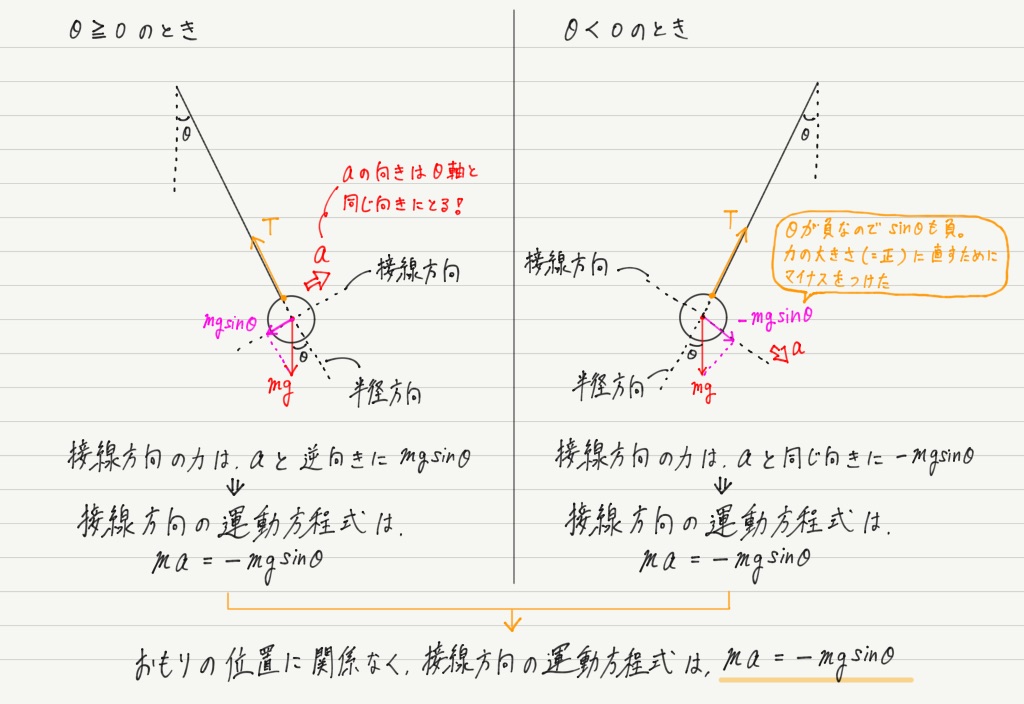
振り子は円運動の一部なので通常ならば半径方向(中心方向)の運動方程式を立てるところですが,今回の目的は接線方向の運動を調べることなので,半径方向は無視して接線方向だけ取り上げます。
おもりにはたらく力は重力と張力の2つだけなので簡単ですね〜
運動方程式が求められたので,これをもとに詳しく調べていきましょう!
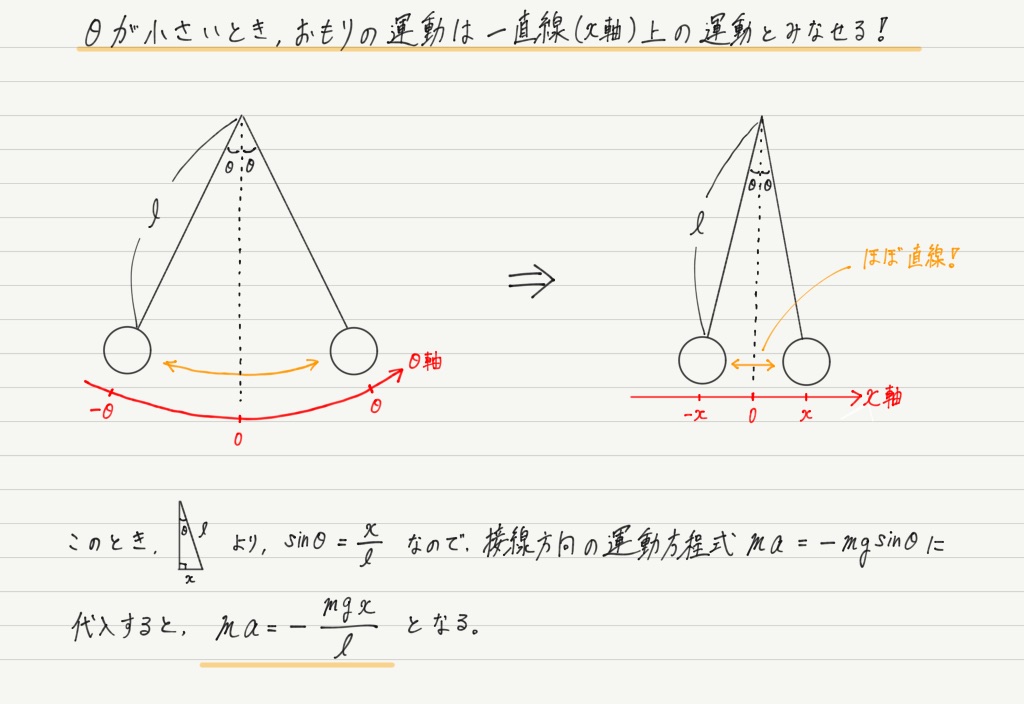
近似による処理
話を簡単にするために次のような条件を課します。
条件:振れ角θは非常に小さいとする。
この条件の下で運動方程式を書き換えると…
sinθがなくなって式が簡単になりました!
…いやいや,そんなことよりももっと重大なことが起こっています。
得られた式をよく見てください。
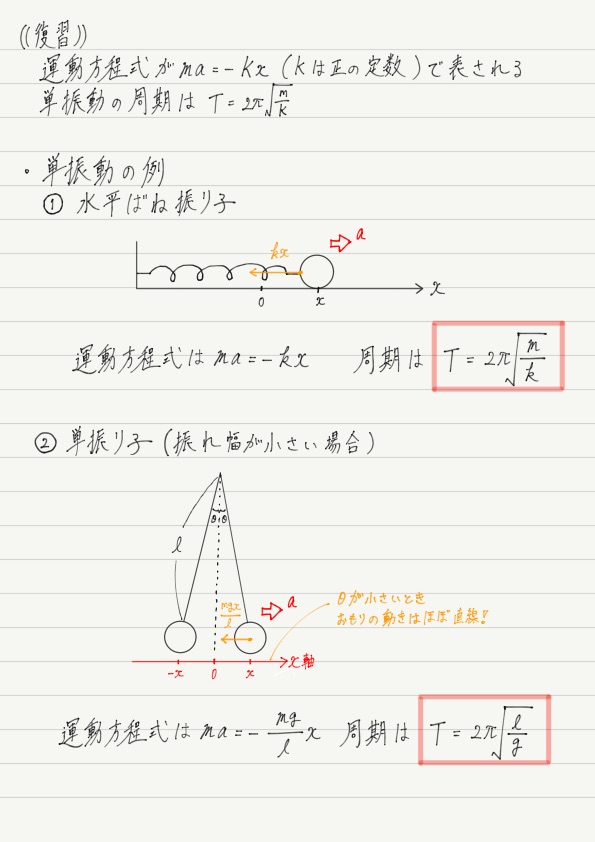
振れ角が小さい単振り子は単振動の例としてよく登場するので,覚えておきましょう!
振り子の等時性
運動方程式が単振動の形になっているということは,周期を求めることが可能です。
公式に当てはめて計算してみると…
単振り子の周期は糸の長さと重力加速度のみで決まり,おもりの質量には無関係(計算の途中でmは約分されてしまった!)であることがこの式から読み取れます。
有名な「振り子の等時性」ってやつですね!
振れ角が大きかったら?
振り子の等時性は有名ではありますが,上で行った計算はすべて振れ角θが非常に小さいとき限定で成り立つことに注意しましょう。
振れ角が大きいとき,等時性は成り立ちません!
小中学校の理科の教科書はやたら等時性を強調してるので,絶対に成り立つと思い込んでいる人が多いように思いますが,条件付きで成り立つ性質であることに注意しましょう。
さて,さっきはθが小さいと仮定して近似計算を行いましたが,中には「近似しないで厳密に解きたい!」という人もいるでしょう。
しかしここで残念なお知らせ。
近似する前の単振り子の運動方程式は初等的には解けないことが知られています。
(※ 初等的に解けない=解がn次関数や三角関数,指数・対数関数などで表せない)
これは高校レベルの数学では解けないと言っているのではなく,原理的に解けないということです。
単振り子は近似しなくても十分シンプルな運動に思えますが,それですら解けないなんてなんだか変な話ですよね。
もちろん解けないからといって人類は解くことを諦めたわけではありませんが,これ以上は数学の話題になってしまうので,ここでは深入りしません。気になる人は各自で調べてみてください。
今回のまとめノート
単振り子に加え,前回のばね振り子の話も書いておきます!
時間に余裕がある人は,ぜひ問題演習にもチャレンジしてみてください! より一層理解が深まります。
次回予告
物理の礎だけあって長丁場だった力学ですが,終わりが見えてきました。
いよいよ最後のトピック,「惑星の運動」に突入です!